Imaginez que vous cherchez à calculer la limite \( \displaystyle\lim_{x \to 0} \frac{\sin x}{x} \). En substituant directement \( x = 0 \), vous obtenez la forme \( \frac{0}{0} \), qui ne nous apprend rien sur la valeur réelle de la limite. C’est précisément dans de telles situations que la règle de L’Hôpital devient un outil indispensable.
Cette règle, publiée en 1696 dans l’ouvrage Analyse des infiniment petits de Guillaume François Antoine de L’Hôpital, permet de lever les formes indéterminées en exploitant les dérivées des fonctions. Elle constitue l’une des méthodes les plus puissantes du calcul différentiel pour déterminer des limites qui semblent inaccessibles par les techniques algébriques classiques.
Dans ce cours, nous allons explorer en profondeur la règle de L’Hôpital : de sa définition rigoureuse à sa démonstration mathématique, en passant par de nombreux exemples pratiques et exercices corrigés adaptés au niveau lycée et première année universitaire.
Définition et Énoncé de la Règle de L’Hôpital
Définition : Règle de L’Hôpital
Soient \( f \) et \( g \) deux fonctions dérivables sur un intervalle ouvert \( I \) contenant un point \( a \) (éventuellement \( a \) peut être \( +\infty \) ou \( -\infty \)), à l’exception peut-être du point \( a \) lui-même.
Si les conditions suivantes sont satisfaites :
- \( \displaystyle\lim_{x \to a} f(x) = 0 \) et \( \displaystyle\lim_{x \to a} g(x) = 0 \) (forme indéterminée 0/0)
- ou \( \displaystyle\lim_{x \to a} f(x) = \pm\infty \) et \( \displaystyle\lim_{x \to a} g(x) = \pm\infty \) (forme indéterminée ∞/∞)
- \( g'(x) \neq 0 \) au voisinage de \( a \) (sauf peut-être en \( a \))
- La limite \( \displaystyle\lim_{x \to a} \frac{f'(x)}{g'(x)} \) existe (finie ou infinie)
Alors on a :
\lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}
\]
Attention importante : La règle de L’Hôpital stipule que l’on peut calculer la limite d’un quotient \( \frac{f}{g} \) en considérant la limite du quotient des dérivées \( \frac{f’}{g’} \). Il ne s’agit pas de calculer la dérivée du quotient \( \left(\frac{f}{g}\right)’ \) !
Les Formes Indéterminées Concernées
La règle de L’Hôpital s’applique directement aux deux formes indéterminées suivantes :
| Forme indéterminée | Condition sur f et g | Exemple typique |
|---|---|---|
| \( \frac{0}{0} \) | \( \lim f(x) = 0 \) et \( \lim g(x) = 0 \) | \( \displaystyle\lim_{x \to 0} \frac{\sin x}{x} \) |
| \( \frac{\infty}{\infty} \) | \( \lim f(x) = \pm\infty \) et \( \lim g(x) = \pm\infty \) | \( \displaystyle\lim_{x \to +\infty} \frac{e^x}{x^2} \) |
D’autres formes indéterminées comme \( 0 \times \infty \), \( \infty – \infty \), \( 0^0 \), \( 1^\infty \) ou \( \infty^0 \) peuvent également être traitées après une transformation algébrique appropriée pour se ramener à l’une des deux formes précédentes.
Hypothèses et Conditions d’Application
Pour appliquer correctement la règle de L’Hôpital, il est crucial de vérifier rigoureusement toutes les hypothèses. Négliger une seule condition peut conduire à des résultats erronés.
Conditions nécessaires
- Dérivabilité : Les fonctions \( f \) et \( g \) doivent être dérivables au voisinage du point \( a \) (excepté peut-être en \( a \) lui-même).
- Forme indéterminée : La limite doit effectivement présenter une forme indéterminée \( \frac{0}{0} \) ou \( \frac{\infty}{\infty} \). Si ce n’est pas le cas, la règle de L’Hôpital ne s’applique pas et peut donner un résultat incorrect.
- Non-annulation de g’ : La dérivée \( g'(x) \) ne doit pas s’annuler au voisinage de \( a \) (sauf éventuellement en \( a \)).
- Existence de la limite des dérivées : La limite \( \displaystyle\lim_{x \to a} \frac{f'(x)}{g'(x)} \) doit exister (elle peut être finie ou infinie). Si cette limite n’existe pas, on ne peut rien conclure sur la limite initiale.
Erreur fréquente : Appliquer la règle sans vérifier qu’il s’agit bien d’une forme indéterminée. Par exemple, pour \( \displaystyle\lim_{x \to 1} \frac{2x^2}{x} \), on a une forme \( \frac{2}{1} = 2 \), donc la règle de L’Hôpital ne doit pas être utilisée. L’appliquer donnerait \( \displaystyle\lim_{x \to 1} \frac{4x}{1} = 4 \), ce qui est faux !
Interprétation Intuitive et Graphique
Pourquoi la règle de L’Hôpital fonctionne-t-elle ? Pour le comprendre intuitivement, revenons à la définition de la dérivée.
Approche Intuitive pour la Forme 0/0
Lorsque \( f(a) = g(a) = 0 \), le quotient \( \frac{f(x)}{g(x)} \) pour \( x \) proche de \( a \) peut s’écrire :
\frac{f(x)}{g(x)} = \frac{f(x) – f(a)}{g(x) – g(a)} = \frac{\frac{f(x) – f(a)}{x – a}}{\frac{g(x) – g(a)}{x – a}}
\]
Or, par définition de la dérivée :
- \( \displaystyle\frac{f(x) – f(a)}{x – a} \) tend vers \( f'(a) \) quand \( x \to a \)
- \( \displaystyle\frac{g(x) – g(a)}{x – a} \) tend vers \( g'(a) \) quand \( x \to a \)
Donc, lorsque \( x \) se rapproche de \( a \), le quotient \( \frac{f(x)}{g(x)} \) se comporte comme \( \frac{f'(a)}{g'(a)} \). C’est l’essence de la règle de L’Hôpital : le comportement local d’un quotient de fonctions s’annulant en un point est gouverné par le quotient de leurs dérivées.
Interprétation Graphique
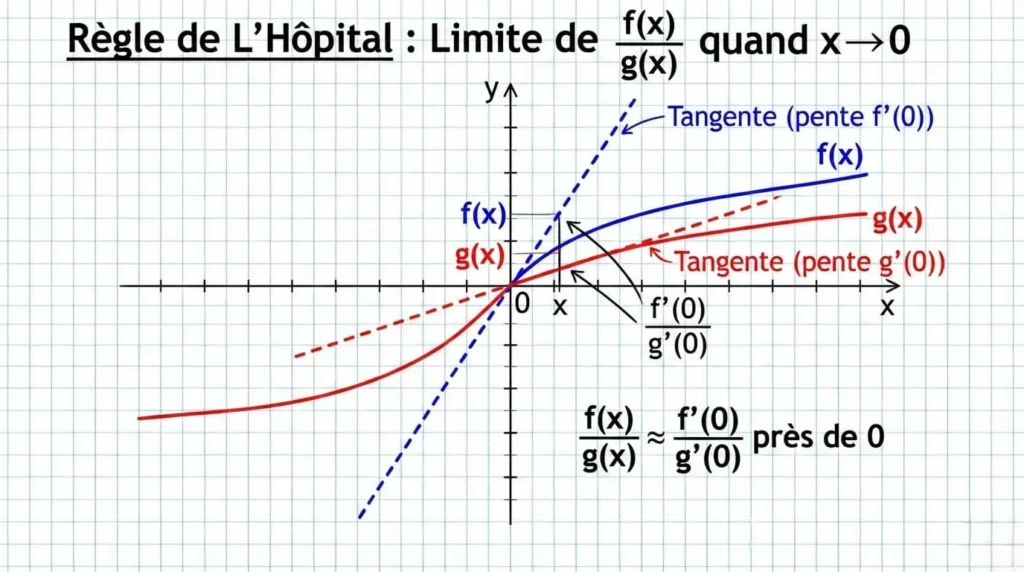
Graphiquement, quand deux courbes partent du même point avec des pentes différentes (données par leurs dérivées), le rapport de leurs hauteurs à proximité de ce point est approximativement égal au rapport de leurs pentes.
Démonstration Mathématique Rigoureuse
La démonstration de la règle de L’Hôpital repose sur le théorème des accroissements finis généralisé, également appelé théorème de Cauchy.
Théorème des Accroissements Finis Généralisé (Théorème de Cauchy)
Soient \( f \) et \( g \) deux fonctions continues sur \( [a, b] \) et dérivables sur \( ]a, b[ \), avec \( g'(x) \neq 0 \) pour tout \( x \in ]a, b[ \).
Alors il existe \( c \in ]a, b[ \) tel que :
\frac{f(b) – f(a)}{g(b) – g(a)} = \frac{f'(c)}{g'(c)}
\]
Démonstration de la Règle de L’Hôpital (Cas 0/0)
Démontrons la règle dans le cas où \( \displaystyle\lim_{x \to a^+} f(x) = \lim_{x \to a^+} g(x) = 0 \) (limite à droite).
Étape 1 : On prolonge \( f \) et \( g \) par continuité en posant \( f(a) = g(a) = 0 \).
Étape 2 : Pour tout \( x \in ]a, b[ \), \( f \) et \( g \) sont continues sur \( [a, x] \) et dérivables sur \( ]a, x[ \). Par le théorème de Cauchy, il existe \( c_x \in ]a, x[ \) tel que :
\frac{f(x) – f(a)}{g(x) – g(a)} = \frac{f'(c_x)}{g'(c_x)}
\]
Puisque \( f(a) = g(a) = 0 \), on a :
\frac{f(x)}{g(x)} = \frac{f'(c_x)}{g'(c_x)}
\]
Étape 3 : Quand \( x \to a^+ \), on a nécessairement \( c_x \to a^+ \) (car \( a < c_x < x \)).
Étape 4 : Par hypothèse, \( \displaystyle\lim_{t \to a^+} \frac{f'(t)}{g'(t)} = \ell \). Par composition de limites :
\lim_{x \to a^+} \frac{f(x)}{g(x)} = \lim_{x \to a^+} \frac{f'(c_x)}{g'(c_x)} = \lim_{t \to a^+} \frac{f'(t)}{g'(t)} = \ell
\]
Ce qui établit la règle de L’Hôpital pour le cas \( \frac{0}{0} \) avec une limite à droite. La démonstration pour une limite à gauche ou bilatérale est similaire. Le cas \( \frac{\infty}{\infty} \) nécessite un changement de variable supplémentaire pour se ramener au cas \( \frac{0}{0} \).
Remarque historique : Bien que cette règle porte le nom de Guillaume de L’Hôpital (1661-1704), elle est en réalité due à son professeur Jean Bernoulli (1667-1748). L’Hôpital avait payé Bernoulli pour recevoir ses découvertes et avait le droit de les publier. En 1921, des notes de cours de Bernoulli datant de 1691-1692 furent découvertes, confirmant qu’il en était le véritable auteur.
Applications Successives de la Règle
Un aspect remarquable de la règle de L’Hôpital est qu’elle peut être appliquée plusieurs fois de suite si, après une première application, on se retrouve encore face à une forme indéterminée.
Principe : Si après avoir calculé \( \displaystyle\lim_{x \to a} \frac{f'(x)}{g'(x)} \), on obtient encore une forme indéterminée \( \frac{0}{0} \) ou \( \frac{\infty}{\infty} \), on peut réappliquer la règle en dérivant à nouveau numérateur et dénominateur :
\lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)} = \lim_{x \to a} \frac{f^{\prime\prime}(x)}{g^{\prime\prime}(x)} = \ldots
\]
On continue ce processus jusqu’à lever l’indétermination ou jusqu’à ce que la règle ne soit plus applicable.
Exemple d’Application Multiple
Calculons \( \displaystyle\lim_{x \to 0} \frac{\cos(2x) – 1}{x^3 + 5x^2} \)
Vérification : Pour \( x = 0 \) : \( \cos(0) – 1 = 0 \) et \( 0 + 0 = 0 \). Forme \( \frac{0}{0} \) ✓
Première application :
\lim_{x \to 0} \frac{\cos(2x) – 1}{x^3 + 5x^2} = \lim_{x \to 0} \frac{-2\sin(2x)}{3x^2 + 10x}
\]
Pour \( x = 0 \) : \( -2\sin(0) = 0 \) et \( 0 + 0 = 0 \). Encore une forme \( \frac{0}{0} \) !
Deuxième application :
\lim_{x \to 0} \frac{-2\sin(2x)}{3x^2 + 10x} = \lim_{x \to 0} \frac{-4\cos(2x)}{6x + 10}
\]
Pour \( x = 0 \) : \( \frac{-4\cos(0)}{0 + 10} = \frac{-4}{10} = -\frac{2}{5} \)
Conclusion : \( \displaystyle\lim_{x \to 0} \frac{\cos(2x) – 1}{x^3 + 5x^2} = -\frac{2}{5} \)
Traitement des Autres Formes Indéterminées
La règle de L’Hôpital s’applique directement aux formes \( \frac{0}{0} \) et \( \frac{\infty}{\infty} \). Pour les autres formes indéterminées, il faut d’abord effectuer une transformation algébrique.
Forme 0 × ∞
Si \( \displaystyle\lim_{x \to a} f(x) = 0 \) et \( \displaystyle\lim_{x \to a} g(x) = \pm\infty \), le produit \( f(x) \cdot g(x) \) présente une forme \( 0 \times \infty \).
Transformation : On réécrit le produit sous forme de quotient :
f(x) \cdot g(x) = \frac{f(x)}{1/g(x)} \quad \text{(forme } \frac{0}{0}\text{)} \quad \text{ou} \quad \frac{g(x)}{1/f(x)} \quad \text{(forme } \frac{\infty}{\infty}\text{)}
\]
Exemple : \( \displaystyle\lim_{x \to 0^+} x \ln x \)
Forme \( 0 \times (-\infty) \). On transforme :
\lim_{x \to 0^+} x \ln x &= \lim_{x \to 0^+} \frac{\ln x}{1/x} \quad \text{(forme } \frac{-\infty}{+\infty}\text{)} \\
&= \lim_{x \to 0^+} \frac{1/x}{-1/x^2} \quad \text{(règle de L’Hôpital)} \\
&= \lim_{x \to 0^+} \frac{x^2}{-x} \\
&= \lim_{x \to 0^+} (-x) = 0
\end{align*}
Forme ∞ – ∞
Pour une différence \( f(x) – g(x) \) où \( \displaystyle\lim f(x) = +\infty \) et \( \displaystyle\lim g(x) = +\infty \), on cherche un dénominateur commun ou une factorisation pour se ramener à \( \frac{0}{0} \) ou \( \frac{\infty}{\infty} \).
Exemple : \( \displaystyle\lim_{x \to +\infty} \left(x – \sqrt{x^2 – x}\right) \)
On multiplie par l’expression conjuguée :
x – \sqrt{x^2 – x} &= \frac{(x – \sqrt{x^2 – x})(x + \sqrt{x^2 – x})}{x + \sqrt{x^2 – x}} \\
&= \frac{x^2 – (x^2 – x)}{x + \sqrt{x^2 – x}} \\
&= \frac{x}{x + \sqrt{x^2 – x}}
\end{align*}
Forme \( \frac{\infty}{\infty} \). On applique L’Hôpital ou on divise par \( x \) :
\lim_{x \to +\infty} \frac{x}{x + \sqrt{x^2 – x}} = \lim_{x \to +\infty} \frac{1}{1 + \sqrt{1 – 1/x}} = \frac{1}{1 + 1} = \frac{1}{2}
\]
Formes Exponentielles : \( 0^0 \), \( 1^\infty \), \( \infty^0 \)
Pour ces formes, on utilise le logarithme pour transformer une puissance en produit :
Si \( L = \displaystyle\lim_{x \to a} [f(x)]^{g(x)} \), on pose \( \ln L = \displaystyle\lim_{x \to a} g(x) \ln f(x) \), ce qui donne souvent une forme \( 0 \times \infty \).
Exemple : \( \displaystyle\lim_{x \to 0^+} x^x \) (forme \( 0^0 \))
\ln L &= \lim_{x \to 0^+} x \ln x = 0 \quad \text{(déjà calculé)} \\
\Rightarrow L &= e^0 = 1
\end{align*}
Exercices Corrigés
Exercice 1 : Forme 0/0 Classique
Énoncé : Calculer \( \displaystyle\lim_{x \to 0} \frac{e^{2x} – 1}{x} \)
Solution détaillée
Étape 1 : Vérification de la forme indéterminée
Pour \( x = 0 \) : \( e^0 – 1 = 0 \) et \( x = 0 \). Forme \( \frac{0}{0} \) ✓
Étape 2 : Application de la règle
Posons \( f(x) = e^{2x} – 1 \) et \( g(x) = x \)
Dérivées : \( f'(x) = 2e^{2x} \) et \( g'(x) = 1 \)
\lim_{x \to 0} \frac{e^{2x} – 1}{x} = \lim_{x \to 0} \frac{2e^{2x}}{1} = 2e^0 = 2
\]
Réponse : La limite vaut 2.
Exercice 2 : Forme ∞/∞
Énoncé : Calculer \( \displaystyle\lim_{x \to +\infty} \frac{\ln(x^2 + 1)}{x} \)
Solution détaillée
Étape 1 : Vérification
Quand \( x \to +\infty \) : \( \ln(x^2 + 1) \to +\infty \) et \( x \to +\infty \). Forme \( \frac{\infty}{\infty} \) ✓
Étape 2 : Dérivation
\( f(x) = \ln(x^2 + 1) \) donc \( f'(x) = \frac{2x}{x^2 + 1} \)
\( g(x) = x \) donc \( g'(x) = 1 \)
\lim_{x \to +\infty} \frac{\ln(x^2 + 1)}{x} &= \lim_{x \to +\infty} \frac{2x/(x^2 + 1)}{1} \\
&= \lim_{x \to +\infty} \frac{2x}{x^2 + 1} \\
&= \lim_{x \to +\infty} \frac{2}{x + 1/x} = 0
\end{align*}
Réponse : La limite vaut 0.
Exercice 3 : Application Multiple
Énoncé : Calculer \( \displaystyle\lim_{x \to 0} \frac{\sin x – x}{x^3} \)
Solution détaillée
Vérification : Forme \( \frac{0}{0} \) ✓
Première application :
\lim_{x \to 0} \frac{\sin x – x}{x^3} = \lim_{x \to 0} \frac{\cos x – 1}{3x^2}
\]
Encore forme \( \frac{0}{0} \) !
Deuxième application :
\lim_{x \to 0} \frac{\cos x – 1}{3x^2} = \lim_{x \to 0} \frac{-\sin x}{6x}
\]
Encore forme \( \frac{0}{0} \) !
Troisième application :
\lim_{x \to 0} \frac{-\sin x}{6x} = \lim_{x \to 0} \frac{-\cos x}{6} = \frac{-1}{6}
\]
Réponse : La limite vaut \( -\frac{1}{6} \).
Exercice 4 : Forme 0 × ∞
Énoncé : Calculer \( \displaystyle\lim_{x \to +\infty} x e^{-x} \)
Solution détaillée
Analyse : Forme \( +\infty \times 0 \)
Transformation :
\lim_{x \to +\infty} x e^{-x} &= \lim_{x \to +\infty} \frac{x}{e^x} \quad \text{(forme } \frac{\infty}{\infty}\text{)} \\
&= \lim_{x \to +\infty} \frac{1}{e^x} \quad \text{(règle de L’Hôpital)} \\
&= 0
\end{align*}
Interprétation : L’exponentielle croît plus vite que toute puissance de \( x \), donc \( e^x \) l’emporte sur \( x \).
Réponse : La limite vaut 0.
Quand NE PAS Utiliser la Règle de L’Hôpital
Bien que puissante, la règle de L’Hôpital n’est pas toujours le meilleur outil. Voici les situations où d’autres méthodes sont préférables :
1. Absence de forme indéterminée
Si la limite se calcule directement, utilisez la substitution !
2. Méthodes algébriques plus simples
Pour \( \displaystyle\lim_{x \to 1} \frac{x^2 – 1}{x – 1} \), factoriser est plus simple que dériver.
3. Disponibilité des développements limités
En mathématiques supérieures, les développements limités (DL) sont souvent plus puissants et systématiques que la règle de L’Hôpital, car ils donnent non seulement la limite mais aussi un équivalent précis.
4. Limites de suites
Pour les suites, privilégiez le théorème de Stolz-Cesàro (équivalent discret de L’Hôpital) ou les techniques propres aux suites.
Lien avec les Taux de Croissance Comparés
La règle de L’Hôpital permet d’établir rigoureusement les croissances comparées des fonctions usuelles. Voici les résultats fondamentaux :
Hiérarchie des Croissances en +∞
Pour tout \( n \in \mathbb{N}^* \) et \( \alpha > 0 \) :
\lim_{x \to +\infty} \frac{\ln x}{x^\alpha} &= 0 \quad &\text{(logarithme < puissance)} \\ \lim_{x \to +\infty} \frac{x^n}{e^x} &= 0 \quad &\text{(puissance < exponentielle)} \\ \lim_{x \to +\infty} \frac{e^x}{x^n} &= +\infty \quad &\text{(exponentielle domine)} \end{align*}
Mnémotechnique : ln < Puissances < Exponentielles
Démonstration avec L’Hôpital : Montrons que \( \displaystyle\lim_{x \to +\infty} \frac{x^2}{e^x} = 0 \)
\lim_{x \to +\infty} \frac{x^2}{e^x} &= \lim_{x \to +\infty} \frac{2x}{e^x} \quad \text{(L’Hôpital, forme } \frac{\infty}{\infty}\text{)} \\
&= \lim_{x \to +\infty} \frac{2}{e^x} \quad \text{(L’Hôpital à nouveau)} \\
&= 0
\end{align*}
Conclusion et Points Clés à Retenir
La règle de L’Hôpital est un outil fondamental du calcul différentiel qui transforme des limites apparemment complexes en problèmes de dérivation. Voici les points essentiels à mémoriser :
- Domaine d’application : Uniquement les formes indéterminées \( \frac{0}{0} \) et \( \frac{\infty}{\infty} \)
- Principe : Remplacer le quotient de fonctions par le quotient de leurs dérivées
- Condition cruciale : Vérifier l’existence de la limite des dérivées
- Applications multiples : Possibilité de dériver plusieurs fois si nécessaire
- Transformations : Les autres formes indéterminées nécessitent une manipulation préalable
- Limitations : La réciproque n’est pas vraie ; ne pas appliquer aveuglément
Maîtriser la règle de L’Hôpital requiert de la pratique et une compréhension solide des dérivées. N’hésitez pas à toujours vérifier les hypothèses avant de l’appliquer, et privilégiez les méthodes algébriques quand elles sont plus simples.
Pour approfondir vos connaissances, consultez également les cours sur le théorème des accroissements finis, les développements limités, et les équivalents de fonctions.