Découvrez l’ensemble des nombres complexes, leur construction, leurs propriétés et leurs applications en mathématiques et en physique. Ce cours détaillé vous accompagne de la définition jusqu’aux formes avancées.
Introduction : Pourquoi les nombres complexes ?
Imaginez que vous cherchez à résoudre l’équation \( x^2 = -1 \). Dans l’ensemble des nombres réels \( \mathbb{R} \), cette équation n’admet aucune solution, car le carré d’un nombre réel est toujours positif ou nul. C’est pour pallier cette limite que les mathématiciens ont introduit les nombres complexes.
Les nombres complexes représentent une extension naturelle de l’ensemble des nombres réels. Ils permettent de résoudre toutes les équations polynomiales, y compris celles qui ne possèdent pas de solutions réelles. Cette extension s’est révélée indispensable non seulement en mathématiques pures, mais également en physique (mécanique quantique, électromagnétisme), en ingénierie et dans de nombreux domaines scientifiques.
Historiquement, les nombres complexes sont apparus au XVIe siècle dans les travaux de mathématiciens italiens comme Cardan, Bombelli et Tartaglia, qui cherchaient à résoudre des équations du troisième degré. Ce n’est qu’au XIXe siècle, avec Gauss, Argand et Cauchy, que leur interprétation géométrique s’est développée, donnant naissance au plan complexe.
Définition de l’ensemble des nombres complexes
Définition fondamentale
On admet l’existence d’un ensemble noté \( \mathbb{C} \), appelé ensemble des nombres complexes, qui vérifie les propriétés suivantes :
- \( \mathbb{C} \) contient l’ensemble des nombres réels \( \mathbb{R} \) : \( \mathbb{R} \subset \mathbb{C} \)
- \( \mathbb{C} \) contient un élément noté \( i \), appelé unité imaginaire, tel que \( i^2 = -1 \)
- Tout élément \( z \) de \( \mathbb{C} \) s’écrit de façon unique sous la forme \( z = a + ib \), où \( a \) et \( b \) sont des nombres réels
- \( \mathbb{C} \) est muni d’une addition et d’une multiplication qui prolongent celles définies sur \( \mathbb{R} \) et possèdent les mêmes propriétés algébriques (associativité, commutativité, distributivité)
L’unité imaginaire i
L’unité imaginaire i est l’élément fondamental qui distingue les nombres complexes des nombres réels. Par définition, on a :
i^2 = -1
\]
Cette propriété permet de résoudre l’équation \( x^2 = -1 \), qui possède désormais deux solutions dans \( \mathbb{C} \) : \( x = i \) et \( x = -i \).
On peut également calculer les puissances successives de \( i \) :
\begin{align*}
i^0 &= 1 \\
i^1 &= i \\
i^2 &= -1 \\
i^3 &= i^2 \cdot i = -i \\
i^4 &= i^2 \cdot i^2 = (-1)(-1) = 1
\end{align*}
\]
On observe que les puissances de \( i \) sont périodiques de période 4. Ainsi, pour tout entier \( n \), on a \( i^{n+4} = i^n \).
Forme algébrique d’un nombre complexe
Forme algébrique
L’écriture \( z = a + ib \), où \( a \) et \( b \) sont des nombres réels, est appelée forme algébrique du nombre complexe \( z \).
Le réel \( a \) est appelé partie réelle de \( z \), notée \( \text{Re}(z) \) ou \( \mathfrak{Re}(z) \).
Le réel \( b \) est appelé partie imaginaire de \( z \), notée \( \text{Im}(z) \) ou \( \mathfrak{Im}(z) \).
Attention : La partie imaginaire est un nombre réel ! Si \( z = 3 + 5i \), alors \( \text{Im}(z) = 5 \) (et non \( 5i \)). Le symbole \( i \) sert uniquement à indiquer quelle composante est la partie imaginaire.
Cas particuliers
- Nombre réel : Un nombre complexe \( z = a + ib \) est réel si et seulement si \( b = 0 \), c’est-à-dire \( \text{Im}(z) = 0 \). Par exemple, \( z = 5 \) est un nombre réel.
- Imaginaire pur : Un nombre complexe \( z = a + ib \) est dit imaginaire pur si et seulement si \( a = 0 \) et \( b \neq 0 \), c’est-à-dire \( \text{Re}(z) = 0 \). Par exemple, \( z = 3i \) est un imaginaire pur.
- Cas particulier du zéro : Le nombre \( 0 \) est le seul nombre complexe qui soit à la fois réel et imaginaire pur.
Égalité de deux nombres complexes
Deux nombres complexes sont égaux si et seulement s’ils ont la même partie réelle et la même partie imaginaire.
Autrement dit, si \( z_1 = a + ib \) et \( z_2 = c + id \) avec \( a, b, c, d \in \mathbb{R} \), alors :
z_1 = z_2 \iff \begin{cases} a = c \\ b = d \end{cases}
\]
Exemple : Déterminer les réels \( x \) et \( y \) tels que \( (2x – 3) + i(y + 1) = 5 – 2i \).
Solution : Par identification des parties réelle et imaginaire :
\begin{cases}
2x – 3 = 5 \\
y + 1 = -2
\end{cases}
\iff
\begin{cases}
x = 4 \\
y = -3
\end{cases}
\]
Opérations sur les nombres complexes
Addition et soustraction
L’addition de deux nombres complexes se fait en additionnant séparément les parties réelles et les parties imaginaires.
Soient \( z_1 = a + ib \) et \( z_2 = c + id \) deux nombres complexes. On a :
z_1 + z_2 = (a + c) + i(b + d)
\]
z_1 – z_2 = (a – c) + i(b – d)
\]
Exemple : Si \( z_1 = 3 + 2i \) et \( z_2 = 1 – 4i \), alors :
z_1 + z_2 = (3 + 1) + i(2 – 4) = 4 – 2i
\]
Multiplication
La multiplication s’effectue en développant le produit et en utilisant la relation \( i^2 = -1 \).
Soient \( z_1 = a + ib \) et \( z_2 = c + id \) deux nombres complexes. On a :
\begin{align*}
z_1 \times z_2 &= (a + ib)(c + id) \\
&= ac + iad + ibc + i^2bd \\
&= ac + iad + ibc – bd \\
&= (ac – bd) + i(ad + bc)
\end{align*}
\]
Exemple : Si \( z_1 = 2 + 3i \) et \( z_2 = 1 – i \), calculons \( z_1 \times z_2 \) :
\begin{align*}
z_1 \times z_2 &= (2 + 3i)(1 – i) \\
&= 2 – 2i + 3i – 3i^2 \\
&= 2 + i + 3 \\
&= 5 + i
\end{align*}
\]
Division
Pour diviser deux nombres complexes, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur.
Conjugué d’un nombre complexe
Conjugué
Soit \( z = a + ib \) un nombre complexe avec \( a, b \in \mathbb{R} \). On appelle conjugué de z, noté \( \overline{z} \), le nombre complexe défini par :
\overline{z} = a – ib
\]
Interprétation géométrique : Le conjugué de \( z \) correspond au symétrique du point d’affixe \( z \) par rapport à l’axe des abscisses dans le plan complexe.
Propriétés du conjugué
Soient \( z \) et \( z’ \) deux nombres complexes. Le conjugué vérifie les propriétés suivantes :
- \( \overline{\overline{z}} = z \) (involutivité)
- \( \overline{z + z’} = \overline{z} + \overline{z’} \)
- \( \overline{z \times z’} = \overline{z} \times \overline{z’} \)
- \( \overline{\left(\frac{z}{z’}\right)} = \frac{\overline{z}}{\overline{z’}} \) (pour \( z’ \neq 0 \))
- \( z + \overline{z} = 2 \text{Re}(z) \)
- \( z – \overline{z} = 2i \text{Im}(z) \)
- \( z \times \overline{z} = a^2 + b^2 \) (nombre réel positif)
Démonstration de la propriété 7
Soit \( z = a + ib \). On a \( \overline{z} = a – ib \). Calculons le produit :
\begin{align*}
z \times \overline{z} &= (a + ib)(a – ib) \\
&= a^2 – iab + iab – i^2b^2 \\
&= a^2 – (-1)b^2 \\
&= a^2 + b^2
\end{align*}
\]
Cette propriété est fondamentale car elle permet de simplifier les divisions de nombres complexes.
Application : division de nombres complexes
Exemple : Calculer \( \frac{3 + 2i}{1 – i} \) sous forme algébrique.
Solution : On multiplie le numérateur et le dénominateur par le conjugué du dénominateur :
\begin{align*}
\frac{3 + 2i}{1 – i} &= \frac{(3 + 2i)(1 + i)}{(1 – i)(1 + i)} \\
&= \frac{3 + 3i + 2i + 2i^2}{1 – i^2} \\
&= \frac{3 + 5i – 2}{1 + 1} \\
&= \frac{1 + 5i}{2} \\
&= \frac{1}{2} + \frac{5}{2}i
\end{align*}
\]
Module d’un nombre complexe
Module
Soit \( z = a + ib \) un nombre complexe avec \( a, b \in \mathbb{R} \). On appelle module de z, noté \( |z| \), le nombre réel positif défini par :
|z| = \sqrt{a^2 + b^2}
\]
Interprétation géométrique : Dans le plan complexe, le module de \( z \) représente la distance entre l’origine \( O \) et le point \( M \) d’affixe \( z \). On a donc \( |z| = OM \).
Remarque : Le module généralise la notion de valeur absolue des nombres réels. En effet, si \( z = a \) est un nombre réel, alors \( |z| = |a| \).
Propriétés du module
Soient \( z \) et \( z’ \) deux nombres complexes. Le module vérifie les propriétés suivantes :
- \( |z| \geq 0 \) et \( |z| = 0 \iff z = 0 \)
- \( |z|^2 = z \times \overline{z} \)
- \( |\overline{z}| = |z| \)
- \( |z \times z’| = |z| \times |z’| \)
- \( \left|\frac{z}{z’}\right| = \frac{|z|}{|z’|} \) (pour \( z’ \neq 0 \))
- Inégalité triangulaire : \( |z + z’| \leq |z| + |z’| \)
Exemple : Si \( z = 3 – 4i \), calculer \( |z| \).
Solution :
|z| = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Représentation géométrique : le plan complexe
On munit le plan d’un repère orthonormé \( (O; \vec{u}, \vec{v}) \). Cette représentation est appelée plan complexe ou plan d’Argand.
Affixe d’un point et d’un vecteur
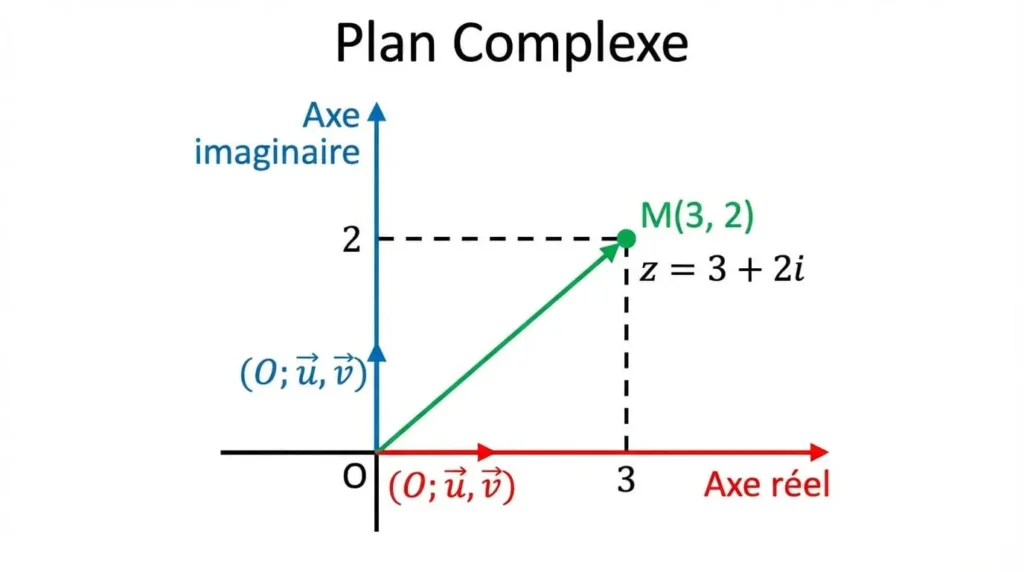
À tout nombre complexe \( z = a + ib \), on associe :
- Le point \( M \) de coordonnées \( (a; b) \), appelé point image de z ou point d’affixe z
- Le vecteur \( \overrightarrow{OM} \) de coordonnées \( (a; b) \), appelé vecteur image de z
Réciproquement, on dit que \( z \) est l’affixe du point \( M \) et du vecteur \( \overrightarrow{OM} \).
Vocabulaire : L’axe des abscisses est appelé axe réel, et l’axe des ordonnées est appelé axe imaginaire.
Propriétés géométriques
Soient \( A \) et \( B \) deux points du plan d’affixe respectives \( z_A \) et \( z_B \). Alors :
- Le vecteur \( \overrightarrow{AB} \) a pour affixe \( z_B – z_A \)
- La distance \( AB \) est donnée par \( AB = |z_B – z_A| \)
- Le milieu \( I \) du segment \( [AB] \) a pour affixe \( \frac{z_A + z_B}{2} \)
Exemple : Soient \( A \) d’affixe \( z_A = 1 + 2i \) et \( B \) d’affixe \( z_B = 4 – i \). Calculer la distance \( AB \).
Solution :
\begin{align*}
AB &= |z_B – z_A| \\
&= |(4 – i) – (1 + 2i)| \\
&= |3 – 3i| \\
&= \sqrt{3^2 + (-3)^2} \\
&= \sqrt{18} = 3\sqrt{2}
\end{align*}
\]
Argument d’un nombre complexe
Argument
Soit \( z \) un nombre complexe non nul, et soit \( M \) son point image dans le plan complexe. On appelle argument de z, noté \( \arg(z) \), toute mesure en radians de l’angle orienté \( (\vec{u}, \overrightarrow{OM}) \).
L’argument est défini à \( 2\pi \) près. On note : \( \arg(z) = \theta \, [2\pi] \).
Remarque : L’argument n’est pas défini pour \( z = 0 \).
Lien avec les coordonnées
Si \( z = a + ib \) avec \( z \neq 0 \), et si \( \theta \) est un argument de \( z \), alors :
\cos(\theta) = \frac{a}{|z|} \quad \text{et} \quad \sin(\theta) = \frac{b}{|z|}
\]
On peut également écrire :
a = |z| \cos(\theta) \quad \text{et} \quad b = |z| \sin(\theta)
\]
Propriétés de l’argument
Soient \( z \) et \( z’ \) deux nombres complexes non nuls. On a :
- \( \arg(z \times z’) = \arg(z) + \arg(z’) \, [2\pi] \)
- \( \arg\left(\frac{z}{z’}\right) = \arg(z) – \arg(z’) \, [2\pi] \)
- \( \arg(\overline{z}) = -\arg(z) \, [2\pi] \)
- \( \arg(z^n) = n \arg(z) \, [2\pi] \) pour \( n \in \mathbb{Z} \)
Exemple : Déterminer un argument de \( z = 1 + i \).
Solution : On calcule le module : \( |z| = \sqrt{1^2 + 1^2} = \sqrt{2} \).
Ensuite :
\cos(\theta) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \quad \text{et} \quad \sin(\theta) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
On reconnaît l’angle \( \theta = \frac{\pi}{4} \). Donc \( \arg(1 + i) = \frac{\pi}{4} \, [2\pi] \).
Forme exponentielle d’un nombre complexe
Forme exponentielle
Soit \( z \) un nombre complexe non nul de module \( r \) et d’argument \( \theta \). La forme exponentielle de \( z \) est :
z = r e^{i\theta}
\]
où \( r = |z| \) et \( \theta = \arg(z) \).
Formule d’Euler
Pour tout nombre réel \( \theta \), on a la formule d’Euler :
e^{i\theta} = \cos(\theta) + i\sin(\theta)
\]
Cette formule fondamentale établit le lien entre la fonction exponentielle et les fonctions trigonométriques.
Lien entre forme algébrique et forme exponentielle
Si \( z = r e^{i\theta} \), alors en utilisant la formule d’Euler :
z = r(\cos(\theta) + i\sin(\theta)) = r\cos(\theta) + i \, r\sin(\theta)
\]
On retrouve donc la forme algébrique avec \( a = r\cos(\theta) \) et \( b = r\sin(\theta) \).
Avantages de la forme exponentielle
La forme exponentielle simplifie considérablement les calculs de produits, quotients et puissances :
- Produit : Si \( z_1 = r_1 e^{i\theta_1} \) et \( z_2 = r_2 e^{i\theta_2} \), alors :\[
z_1 \times z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)}
\] - Quotient :\[
\frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\theta_1 – \theta_2)}
\] - Puissance :\[
z^n = r^n e^{in\theta}
\]
Exemple : Calculer \( (1 + i)^{10} \) en utilisant la forme exponentielle.
Solution : On sait que \( 1 + i = \sqrt{2} e^{i\frac{\pi}{4}} \). Donc :
\begin{align*}
(1 + i)^{10} &= \left(\sqrt{2} e^{i\frac{\pi}{4}}\right)^{10} \\
&= (\sqrt{2})^{10} e^{i \frac{10\pi}{4}} \\
&= 2^5 e^{i \frac{5\pi}{2}} \\
&= 32 e^{i\frac{\pi}{2}} \\
&= 32(\cos(\frac{\pi}{2}) + i\sin(\frac{\pi}{2})) \\
&= 32(0 + i) \\
&= 32i
\end{align*}
\]
Équations du second degré dans les complexes
L’un des intérêts majeurs des nombres complexes est qu’ils permettent de résoudre toutes les équations du second degré, y compris celles qui n’ont pas de solutions réelles.
Résolution dans ℂ
Soit l’équation du second degré \( az^2 + bz + c = 0 \) avec \( a, b, c \in \mathbb{C} \) et \( a \neq 0 \).
On calcule le discriminant \( \Delta = b^2 – 4ac \).
- Si \( \Delta = 0 \), l’équation admet une solution double : \( z_0 = -\frac{b}{2a} \)
- Si \( \Delta \neq 0 \), on détermine un nombre complexe \( \delta \) tel que \( \delta^2 = \Delta \). L’équation admet alors deux solutions distinctes :\[
z_1 = \frac{-b – \delta}{2a} \quad \text{et} \quad z_2 = \frac{-b + \delta}{2a}
\]
Cas particulier : coefficients réels
Lorsque les coefficients \( a, b, c \) sont réels, on distingue trois cas selon le signe du discriminant :
- Si \( \Delta > 0 \) : deux solutions réelles distinctes \( z_1 = \frac{-b – \sqrt{\Delta}}{2a} \) et \( z_2 = \frac{-b + \sqrt{\Delta}}{2a} \)
- Si \( \Delta = 0 \) : une solution réelle double \( z_0 = -\frac{b}{2a} \)
- Si \( \Delta < 0 \) : deux solutions complexes conjuguées. On pose \( \delta = i\sqrt{-\Delta} \), d’où :\[
z_1 = \frac{-b – i\sqrt{-\Delta}}{2a} \quad \text{et} \quad z_2 = \frac{-b + i\sqrt{-\Delta}}{2a}
\]
Remarque importante : Lorsque les coefficients sont réels et que \( \Delta < 0 \), les deux solutions sont conjuguées : \( z_2 = \overline{z_1} \).
Conclusion
Les nombres complexes constituent une extension naturelle et nécessaire de l’ensemble des nombres réels. Leur introduction permet de résoudre toutes les équations du second degré et plus généralement, toutes les équations polynomiales grâce au théorème fondamental de l’algèbre.
Nous avons vu que les nombres complexes peuvent être représentés sous plusieurs formes complémentaires :
- La forme algébrique \( z = a + ib \), pratique pour les additions et soustractions
- La forme exponentielle \( z = r e^{i\theta} \), idéale pour les multiplications, divisions et puissances
- La représentation géométrique dans le plan complexe, qui donne une intuition visuelle
Les notions de conjugué, module et argument permettent de manipuler efficacement ces nombres et de résoudre une grande variété de problèmes mathématiques et physiques.
La maîtrise des nombres complexes est indispensable pour aborder sereinement les études scientifiques supérieures, que ce soit en mathématiques, physique, chimie ou ingénierie. Ils constituent un langage universel qui unifie de nombreux concepts apparemment distincts.