Définition et fondements historiques de la trigonométrie
Définition : La trigonométrie est la branche des mathématiques qui étudie les relations entre les angles et les côtés des triangles, particulièrement les triangles rectangles. Son nom provient du grec ancien trígōnon (triangle) et métron (mesure).
Les origines de la trigonométrie remontent au troisième siècle avant J.-C., lorsque les mathématiciens grecs comme Euclide et Archimède étudiaient les propriétés des cordes inscrites dans les cercles. Hipparque de Nicée établit les premières tables de cordes, ancêtres de nos tables trigonométriques actuelles. Au cinquième siècle après J.-C., les mathématiciens indiens développèrent le concept de sinus, tandis que les savants persans et arabes perfectionnèrent l’ensemble des six fonctions trigonométriques.
Le mathématicien allemand Regiomontanus rédigea au quinzième siècle l’un des premiers traités européens sur le sujet, intitulé De Triangulis. Le terme « trigonométrie » fut utilisé pour la première fois par Bartholomaeus Pitiscus en 1595 dans son ouvrage Trigonometria. Depuis lors, cette discipline n’a cessé d’évoluer pour devenir un pilier des mathématiques modernes, essentielle dans l’enseignement secondaire et universitaire français.
Les trois fonctions trigonométriques dans le triangle rectangle
Dans un triangle rectangle, trois rapports fondamentaux relient les angles aigus aux longueurs des côtés. Ces rapports définissent les trois fonctions trigonométriques principales : le cosinus, le sinus et la tangente.
Vocabulaire du triangle rectangle
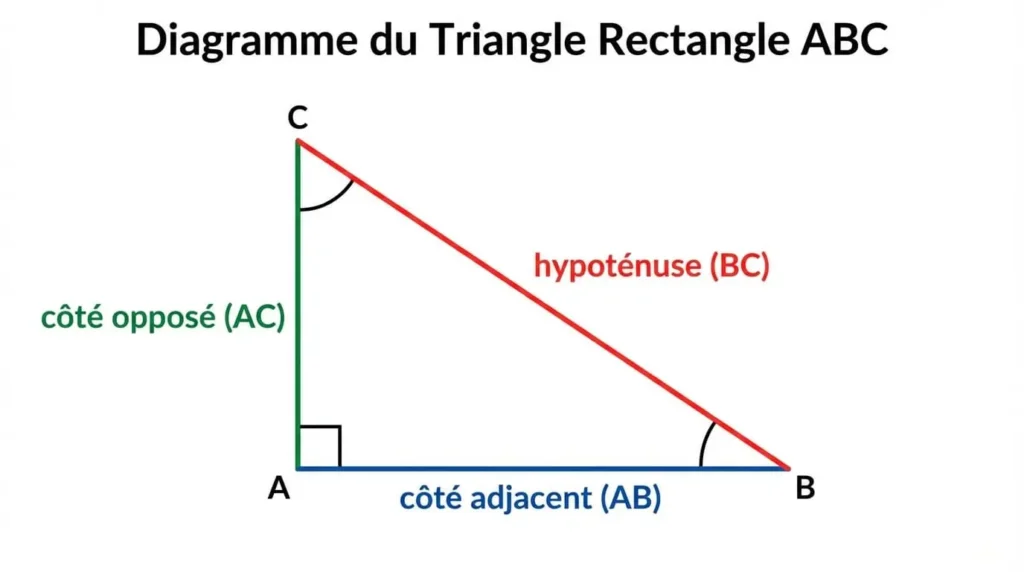
Considérons un triangle rectangle ABC, rectangle en A. On distingue trois côtés particuliers :
- L’hypoténuse : le côté le plus long, opposé à l’angle droit (le côté [BC])
- Le côté adjacent à un angle aigu : le côté qui forme l’angle avec l’hypoténuse
- Le côté opposé à un angle aigu : le côté qui fait face à cet angle
Le cosinus d’un angle aigu
Dans un triangle rectangle, le cosinus d’un angle aigu est égal au rapport de la longueur du côté adjacent à cet angle par la longueur de l’hypoténuse.
\cos(\alpha) = \frac{\text{Côté adjacent}}{\text{Hypoténuse}}
\]
Propriétés du cosinus :
- Le cosinus d’un angle aigu est toujours compris entre 0 et 1
- Il s’agit d’un nombre sans dimension (rapport de deux longueurs)
- Le cosinus ne peut être calculé pour un angle droit
- Plus l’angle est petit, plus son cosinus est proche de 1
Le sinus d’un angle aigu
Dans un triangle rectangle, le sinus d’un angle aigu est égal au rapport de la longueur du côté opposé à cet angle par la longueur de l’hypoténuse.
\sin(\alpha) = \frac{\text{Côté opposé}}{\text{Hypoténuse}}
\]
Le sinus d’un angle aigu dans un triangle rectangle est également toujours compris entre 0 et 1. Cette fonction est complémentaire au cosinus : pour deux angles aigus d’un même triangle rectangle, le sinus de l’un égale le cosinus de l’autre.
La tangente d’un angle aigu
Dans un triangle rectangle, la tangente d’un angle aigu est égale au rapport de la longueur du côté opposé à cet angle par la longueur du côté adjacent.
\tan(\alpha) = \frac{\text{Côté opposé}}{\text{Côté adjacent}}
\]
Contrairement au sinus et au cosinus, la tangente n’est pas limitée à l’intervalle [0, 1]. Elle peut prendre toute valeur positive pour un angle aigu. La tangente s’exprime également en fonction du sinus et du cosinus :
\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \quad (\text{si } \cos(\alpha) \neq 0)
\]
Astuce mnémotechnique : Retenez la formule CAH-SOH-TOA :
Cosinus = Adjacent / Hypoténuse
Sinus = Opposé / Hypoténuse
Tangente = Opposé / Adjacent
Le cercle trigonométrique et ses propriétés
Le cercle trigonométrique représente un outil fondamental pour étendre les définitions des fonctions trigonométriques au-delà des angles aigus. Il permet de travailler avec tous les angles réels et constitue la base de l’étude approfondie de la trigonométrie.
Construction et équation du cercle trigonométrique
Le cercle trigonométrique est le cercle de centre O (origine du repère orthonormé) et de rayon 1, orienté dans le sens trigonométrique (sens inverse des aiguilles d’une montre, appelé sens direct).
Dans un repère orthonormé \((O, \vec{i}, \vec{j})\), ce cercle possède pour équation cartésienne :
x^2 + y^2 = 1
\]
Le périmètre de ce cercle vaut exactement \(2\pi\) unités, propriété qui permet d’introduire le radian comme unité naturelle de mesure des angles. Cette mesure angulaire s’avère particulièrement adaptée aux calculs mathématiques et physiques.
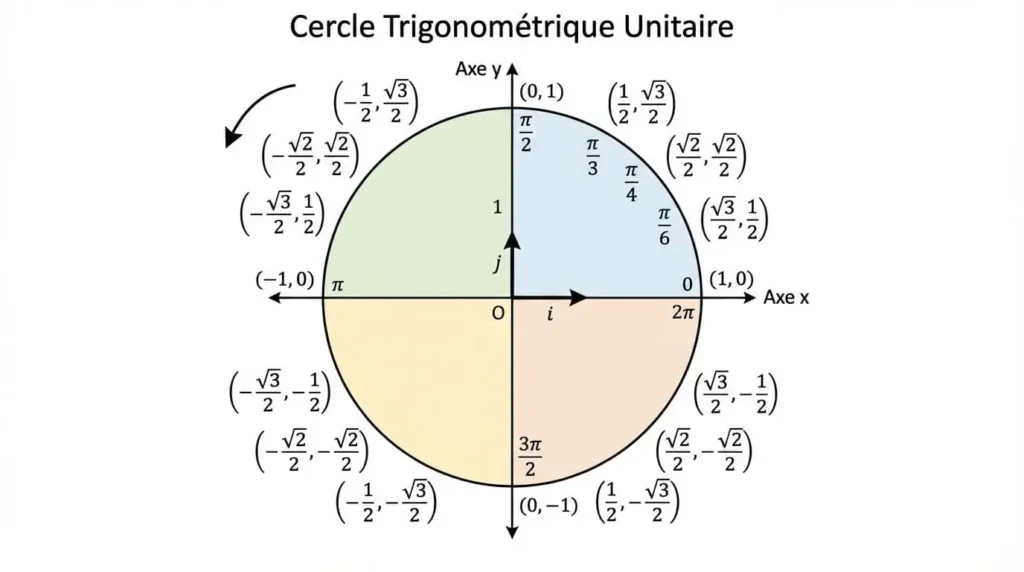
Le radian : unité de mesure angulaire
Le radian est l’unité de mesure d’angle dans le système international. Un angle de 1 radian correspond à l’angle au centre qui intercepte sur le cercle trigonométrique un arc de longueur égale à 1 (le rayon du cercle).
Pour un point M sur le cercle trigonométrique, la mesure en radians de l’angle \(\widehat{AOM}\) (où A est le point de coordonnées (1, 0)) correspond à la longueur de l’arc orienté \(\stackrel{\frown}{AM}\).
Les conversions essentielles entre degrés et radians sont :
| Degrés | Radians | Fraction du cercle |
|---|---|---|
| 360° | \(2\pi\) | Tour complet |
| 180° | \(\pi\) | Demi-tour |
| 90° | \(\frac{\pi}{2}\) | Quart de tour |
| 60° | \(\frac{\pi}{3}\) | Sixième de tour |
| 45° | \(\frac{\pi}{4}\) | Huitième de tour |
| 30° | \(\frac{\pi}{6}\) | Douzième de tour |
Les formules de conversion s’écrivent :
\begin{align*}
\text{Radians} &= \text{Degrés} \times \frac{\pi}{180}\\
\\
\text{Degrés} &= \text{Radians} \times \frac{180}{\pi}
\end{align*}
\]
Coordonnées d’un point sur le cercle trigonométrique
Sur le cercle trigonométrique, pour tout nombre réel \(\theta\), le point M du cercle tel que la mesure de l’angle orienté \((\vec{i}, \overrightarrow{OM})\) vaut \(\theta\) possède pour coordonnées :
M(\cos \theta, \sin \theta)
\]
Cette définition géométrique établit que :
- L’abscisse du point M représente le cosinus de l’angle \(\theta\)
- L’ordonnée du point M représente le sinus de l’angle \(\theta\)
Cette représentation permet de visualiser immédiatement plusieurs propriétés importantes : le cosinus et le sinus sont bornés entre -1 et 1, ils varient de manière continue, et leurs valeurs se répètent après un tour complet (périodicité de \(2\pi\)).
Valeurs trigonométriques des angles remarquables
Les angles remarquables sont des angles particuliers dont les valeurs trigonométriques s’expriment exactement à l’aide de fractions et de racines carrées. La connaissance de ces valeurs est indispensable pour tout étudiant.
| Angle (rad) | Angle (°) | \(\cos\) | \(\sin\) | \(\tan\) |
|---|---|---|---|---|
| \(0\) | 0° | \(1\) | \(0\) | \(0\) |
| \(\frac{\pi}{6}\) | 30° | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{3}\) |
| \(\frac{\pi}{4}\) | 45° | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(1\) |
| \(\frac{\pi}{3}\) | 60° | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\sqrt{3}\) |
| \(\frac{\pi}{2}\) | 90° | \(0\) | \(1\) | Non définie |
| \(\pi\) | 180° | \(-1\) | \(0\) | \(0\) |
| \(\frac{3\pi}{2}\) | 270° | \(0\) | \(-1\) | Non définie |
| \(2\pi\) | 360° | \(1\) | \(0\) | \(0\) |
Méthode de mémorisation : Pour les angles du premier quadrant (0 à π/2), les valeurs du sinus suivent la progression \(\frac{\sqrt{0}}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\). Les valeurs du cosinus suivent cette même séquence dans l’ordre inverse.
Identités trigonométriques remarquables
Les identités trigonométriques sont des égalités mathématiques vérifiées pour toutes les valeurs admissibles de la variable. Elles constituent des outils essentiels pour simplifier des expressions et résoudre des équations.
L’identité pythagoricienne
Théorème fondamental : Pour tout nombre réel \(\theta\), on a :
\cos^2 \theta + \sin^2 \theta = 1
\]
Démonstration : Soit M un point du cercle trigonométrique de coordonnées \((\cos \theta, \sin \theta)\). Puisque M appartient au cercle d’équation \(x^2 + y^2 = 1\), on obtient directement \(\cos^2 \theta + \sin^2 \theta = 1\). Cette relation découle donc du théorème de Pythagore appliqué au triangle rectangle formé par O, M et sa projection sur l’axe des abscisses.
Cette identité permet de calculer une fonction trigonométrique à partir de l’autre. Par exemple, si \(\cos \theta = \frac{3}{5}\), alors :
\sin^2 \theta = 1 – \cos^2 \theta = 1 – \frac{9}{25} = \frac{16}{25}
\]
D’où \(\sin \theta = \pm \frac{4}{5}\), le signe dépendant du quadrant dans lequel se situe l’angle.
Relations dérivées de l’identité pythagoricienne
En divisant l’identité pythagoricienne par \(\cos^2 \theta\) (lorsque \(\cos \theta \neq 0\)), on obtient :
1 + \tan^2 \theta = \frac{1}{\cos^2 \theta}
\]
De même, en divisant par \(\sin^2 \theta\) (lorsque \(\sin \theta \neq 0\)) :
1 + \cot^2 \theta = \frac{1}{\sin^2 \theta}
\]
Formules des angles associés
Les formules des angles associés permettent de réduire l’étude des fonctions trigonométriques au premier quadrant en exploitant les symétries du cercle trigonométrique.
Angles opposés :
\begin{align*}
\cos(-\theta) &= \cos \theta\\
\sin(-\theta) &= -\sin \theta\\
\tan(-\theta) &= -\tan \theta
\end{align*}
\]
Angles supplémentaires :
\begin{align*}
\cos(\pi – \theta) &= -\cos \theta\\
\sin(\pi – \theta) &= \sin \theta\\
\tan(\pi – \theta) &= -\tan \theta
\end{align*}
\]
Angles décalés de π :
\begin{align*}
\cos(\pi + \theta) &= -\cos \theta\\
\sin(\pi + \theta) &= -\sin \theta\\
\tan(\pi + \theta) &= \tan \theta
\end{align*}
\]
Angles complémentaires :
\begin{align*}
\cos\left(\frac{\pi}{2} – \theta\right) &= \sin \theta\\
\sin\left(\frac{\pi}{2} – \theta\right) &= \cos \theta\\
\tan\left(\frac{\pi}{2} – \theta\right) &= \cot \theta = \frac{1}{\tan \theta}
\end{align*}
\]
Formules d’addition
Les formules d’addition permettent d’exprimer les fonctions trigonométriques d’une somme ou d’une différence d’angles en fonction des fonctions trigonométriques de ces angles pris séparément.
Théorème : Pour tous nombres réels \(a\) et \(b\), on a :
\begin{align*}
\cos(a + b) &= \cos a \cos b – \sin a \sin b\\
\cos(a – b) &= \cos a \cos b + \sin a \sin b\\
\\
\sin(a + b) &= \sin a \cos b + \cos a \sin b\\
\sin(a – b) &= \sin a \cos b – \cos a \sin b\\
\\
\tan(a + b) &= \frac{\tan a + \tan b}{1 – \tan a \tan b}\\
\tan(a – b) &= \frac{\tan a – \tan b}{1 + \tan a \tan b}
\end{align*}
\]
Formules de duplication
En posant \(b = a\) dans les formules d’addition, on obtient les formules de duplication (ou formules de l’angle double) :
\begin{align*}
\cos(2a) &= \cos^2 a – \sin^2 a\\
&= 2\cos^2 a – 1\\
&= 1 – 2\sin^2 a\\
\\
\sin(2a) &= 2\sin a \cos a\\
\\
\tan(2a) &= \frac{2\tan a}{1 – \tan^2 a}
\end{align*}
\]
Ces formules permettent d’exprimer \(\cos^2 a\) et \(\sin^2 a\) en fonction de \(\cos(2a)\), ce qui s’avère particulièrement utile en calcul intégral :
\begin{align*}
\cos^2 a &= \frac{1 + \cos(2a)}{2}\\
\\
\sin^2 a &= \frac{1 – \cos(2a)}{2}
\end{align*}
\]
Équations et inéquations trigonométriques
Résolution des équations trigonométriques élémentaires
Pour résoudre une équation du type \(\cos x = k\), \(\sin x = k\) ou \(\tan x = k\), on utilise le cercle trigonométrique et les propriétés de périodicité des fonctions trigonométriques.
Théorème : Soient \(x\) et \(y\) deux nombres réels. Alors :
- \(\cos x = \cos y \iff x \equiv y \, [2\pi] \text{ ou } x \equiv -y \, [2\pi]\)
- \(\sin x = \sin y \iff x \equiv y \, [2\pi] \text{ ou } x \equiv \pi – y \, [2\pi]\)
- \(\tan x = \tan y \iff x \equiv y \, [\pi]\)
Méthode de résolution : Résolvons l’équation \(\cos x = \frac{\sqrt{2}}{2}\) sur l’intervalle \([0, 2\pi]\).
On reconnaît \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\). D’après les propriétés de symétrie du cercle trigonométrique, le cosinus prend cette valeur pour deux angles dans \([0, 2\pi]\) :
x = \frac{\pi}{4} \quad \text{ou} \quad x = 2\pi – \frac{\pi}{4} = \frac{7\pi}{4}
\]
L’ensemble des solutions sur \([0, 2\pi]\) est donc \(S = \left\{\frac{\pi}{4}, \frac{7\pi}{4}\right\}\).
Résolution d’équations trigonométriques plus complexes
Certaines équations nécessitent des transformations algébriques préalables. Par exemple, pour résoudre \(2\cos^2 x – \cos x – 1 = 0\), on pose \(X = \cos x\) et on résout l’équation du second degré \(2X^2 – X – 1 = 0\).
Le discriminant vaut \(\Delta = 1 + 8 = 9\), donc les solutions de l’équation en \(X\) sont :
X_1 = \frac{1 + 3}{4} = 1 \quad \text{et} \quad X_2 = \frac{1 – 3}{4} = -\frac{1}{2}
\]
On résout ensuite \(\cos x = 1\) et \(\cos x = -\frac{1}{2}\) séparément sur l’intervalle souhaité.
Applications de la trigonométrie dans les sciences
La trigonométrie trouve des applications dans de nombreux domaines scientifiques et techniques. Loin d’être une simple abstraction mathématique, elle constitue un outil indispensable pour modéliser et analyser des phénomènes réels.
Navigation et géolocalisation
Depuis l’Antiquité, les marins utilisent la trigonométrie pour déterminer leur position en mer. La navigation astronomique repose sur la mesure d’angles entre les astres et l’horizon. Les systèmes de positionnement par satellite (GPS) emploient la triangulation, méthode qui utilise les principes trigonométriques pour calculer précisément les coordonnées géographiques d’un point à partir des distances mesurées depuis plusieurs satellites.
Architecture et génie civil
Les ingénieurs et architectes appliquent quotidiennement la trigonométrie pour calculer les dimensions structurales, déterminer les angles de toiture, évaluer la stabilité des constructions. Le calcul des pentes, des rampes d’accès, des escaliers, des arcs et des voûtes fait systématiquement appel aux rapports trigonométriques. Les calculs de résistance des matériaux nécessitent également la décomposition des forces en composantes, opération qui repose sur le cosinus et le sinus.
Physique et phénomènes ondulatoires
En physique, les fonctions trigonométriques décrivent naturellement les phénomènes périodiques et ondulatoires. Les oscillations mécaniques (pendules, ressorts), les ondes sonores, les ondes électromagnétiques (lumière, radio), toutes se modélisent à l’aide de fonctions sinusoïdales. L’équation d’une onde progressive sinusoïdale s’écrit typiquement sous la forme :
y(x, t) = A \sin(kx – \omega t + \varphi)
\]
où \(A\) représente l’amplitude, \(k\) le nombre d’onde, \(\omega\) la pulsation et \(\varphi\) la phase initiale.
Astronomie et cosmologie
L’astronomie, discipline qui a vu naître la trigonométrie, continue de l’utiliser intensivement. La méthode de la parallaxe trigonométrique permet de mesurer les distances aux étoiles proches. Les calculs d’éphémérides (positions des planètes et satellites) font appel à des formules trigonométriques complexes. La trigonométrie sphérique, extension de la trigonométrie plane, s’avère indispensable pour les calculs sur la sphère céleste.
Technologies numériques
L’infographie tridimensionnelle et les jeux vidéo utilisent massivement la trigonométrie pour calculer les rotations, les projections perspectives, les transformations géométriques. Les algorithmes de traitement du signal reposent sur la transformée de Fourier, qui décompose un signal quelconque en somme de fonctions sinusoïdales. Les systèmes de synthèse sonore exploitent ces mêmes principes pour générer et manipuler des sons.
Méthodes de calcul en trigonométrie
Détermination d’une longueur dans un triangle rectangle
Lorsqu’on connaît un angle et une longueur dans un triangle rectangle, on peut déterminer les autres longueurs en choisissant la fonction trigonométrique appropriée selon les données disponibles.
Exemple : Dans un triangle ABC rectangle en A, on connaît \(\widehat{ABC} = 35°\) et l’hypoténuse BC = 12 cm. Calculons AB.
AB est adjacent à l’angle \(\widehat{ABC}\) et BC est l’hypoténuse, donc on utilise le cosinus :
\begin{align*}
\cos(\widehat{ABC}) &= \frac{AB}{BC}\\
\\
\cos(35°) &= \frac{AB}{12}\\
\\
AB &= 12 \times \cos(35°) \approx 12 \times 0{,}819 \approx 9{,}83 \text{ cm}
\end{align*}
\]
Détermination d’un angle dans un triangle rectangle
Lorsqu’on connaît deux longueurs d’un triangle rectangle, on détermine la mesure d’un angle en utilisant les fonctions réciproques : arc cosinus, arc sinus ou arc tangente.
Exemple : Dans un triangle DEF rectangle en E, on a DE = 7 cm et DF = 10 cm (hypoténuse). Calculons \(\widehat{EDF}\).
\begin{align*}
\cos(\widehat{EDF}) &= \frac{DE}{DF} = \frac{7}{10} = 0{,}7\\
\\
\widehat{EDF} &= \arccos(0{,}7) \approx 45{,}6°
\end{align*}
\]
Erreur fréquente : Vérifiez toujours le mode de votre calculatrice (DEG pour les degrés, RAD pour les radians) avant d’effectuer un calcul trigonométrique. Une confusion entre ces deux modes constitue l’erreur la plus courante en trigonométrie.
Simplification d’expressions trigonométriques
Pour simplifier une expression trigonométrique, on applique les identités remarquables de manière stratégique. Par exemple, simplifions l’expression :
E = \frac{1 – \cos^2 x}{\sin x}
\]
On utilise l’identité pythagoricienne \(1 – \cos^2 x = \sin^2 x\) :
E = \frac{\sin^2 x}{\sin x} = \sin x \quad (\text{si } \sin x \neq 0)
\]
Résumé du cours de trigonométrie
Ce cours complet de trigonométrie a couvert l’ensemble des concepts fondamentaux nécessaires à la maîtrise de cette discipline mathématique essentielle. Voici les points clés à retenir :
- Les trois fonctions trigonométriques dans le triangle rectangle : Le cosinus représente le rapport entre le côté adjacent et l’hypoténuse, le sinus correspond au rapport entre le côté opposé et l’hypoténuse, et la tangente égale le rapport entre le côté opposé et le côté adjacent. Ces rapports permettent de calculer des longueurs et des angles.
- Le cercle trigonométrique : Cette représentation géométrique fondamentale étend les définitions des fonctions trigonométriques à tous les angles réels. Sur ce cercle de rayon 1, tout point M correspond à un angle θ et possède pour coordonnées (cos θ, sin θ).
- Les angles remarquables : Les valeurs exactes du cosinus, du sinus et de la tangente pour les angles 0, π/6, π/4, π/3, π/2, π, 3π/2 et 2π constituent des références indispensables. Leur mémorisation facilite grandement la résolution d’exercices et d’équations.
- L’identité pythagoricienne fondamentale : Pour tout angle θ, la relation cos²θ + sin²θ = 1 découle directement de l’équation du cercle trigonométrique et du théorème de Pythagore. Elle permet de calculer une fonction trigonométrique à partir de l’autre.
- Les formules des angles associés : Les relations entre les valeurs trigonométriques des angles opposés, supplémentaires et complémentaires exploitent les symétries du cercle trigonométrique pour simplifier les calculs.
- Les formules d’addition et de duplication : Ces identités permettent d’exprimer cos(a + b), sin(a + b), cos(2a) et sin(2a) en fonction des valeurs trigonométriques des angles a et b pris séparément, outils puissants pour la simplification d’expressions complexes.
- La résolution d’équations trigonométriques : En utilisant le cercle trigonométrique, les propriétés de périodicité et les identités remarquables, on peut résoudre méthodiquement des équations du type cos x = k, sin x = k ou des équations plus complexes nécessitant des transformations algébriques.
- Les applications pratiques : La trigonométrie trouve des applications concrètes en navigation, architecture, physique ondulatoire, astronomie, géolocalisation, infographie 3D, traitement du signal et dans de nombreux autres domaines scientifiques et technologiques.
La maîtrise de ces concepts constitue un prérequis indispensable pour les études supérieures scientifiques et techniques. La trigonométrie développe des compétences en raisonnement mathématique, en visualisation géométrique et en résolution de problèmes qui s’avèrent utiles bien au-delà du cadre strictement mathématique.