Le théorème de Pythagore constitue l’un des piliers fondamentaux de la géométrie euclidienne. Enseigné dès le collège, ce théorème établit une relation mathématique élégante entre les côtés d’un triangle rectangle. Bien plus qu’une simple formule à mémoriser, il représente un outil indispensable pour résoudre une multitude de problèmes géométriques et trouve des applications concrètes dans des domaines aussi variés que l’architecture, la navigation ou l’ingénierie. Dans ce cours complet, nous explorerons en profondeur ce théorème millénaire, sa démonstration, sa réciproque, ainsi que ses utilisations pratiques à travers des exercices détaillés.
Définition du théorème de Pythagore
Théorème de Pythagore : Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Avant d’approfondir ce théorème, clarifions quelques termes essentiels relatifs au triangle rectangle.
Vocabulaire du triangle rectangle
Un triangle rectangle possède trois éléments caractéristiques qu’il est crucial de savoir identifier correctement :
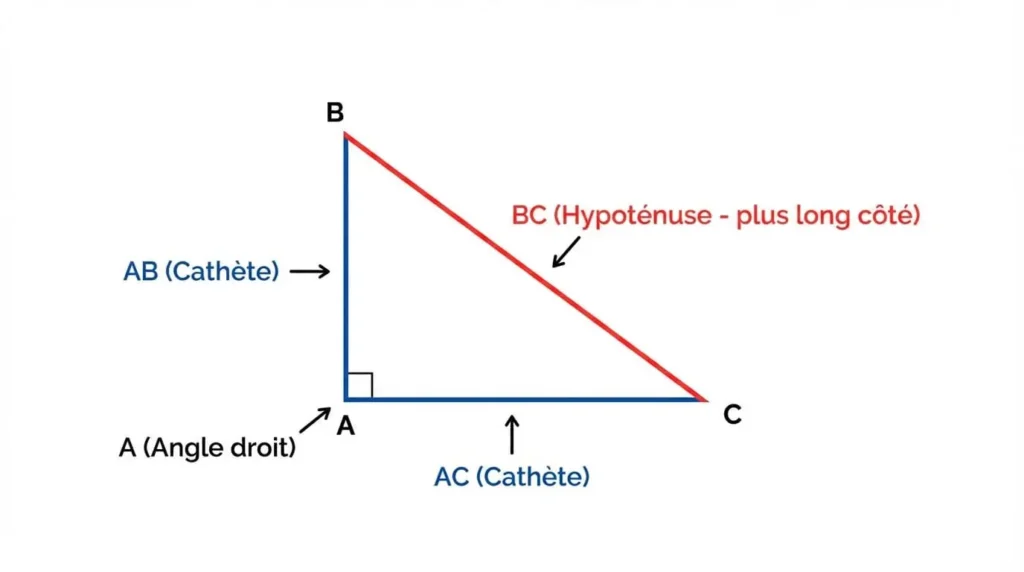
- L’angle droit : C’est l’angle qui mesure exactement 90 degrés. Il est généralement représenté par un petit carré dans les schémas géométriques.
- L’hypoténuse : Il s’agit du côté le plus long du triangle rectangle, celui qui est opposé à l’angle droit. Dans la formule du théorème de Pythagore, c’est ce côté dont on calcule le carré à part.
- Les cathètes (ou côtés de l’angle droit) : Ce sont les deux côtés qui forment l’angle droit. Leurs longueurs sont toujours inférieures à celle de l’hypoténuse.
Formulation mathématique
Considérons un triangle rectangle ABC, rectangle en A. Si on note \( a \) et \( b \) les longueurs des cathètes, et \( c \) la longueur de l’hypoténuse, alors le théorème de Pythagore s’exprime par la formule suivante :
En notation plus explicite, si le triangle ABC est rectangle en A, avec BC comme hypoténuse, on écrit :
Cette relation fondamentale, appelée égalité de Pythagore, permet de calculer la longueur d’un côté du triangle lorsque les deux autres sont connues.
Contexte historique et origines
Bien que ce théorème porte le nom du mathématicien grec Pythagore de Samos (vers 570-495 av. J.-C.), son histoire remonte bien plus loin dans le temps. Les recherches historiques révèlent que cette relation mathématique était déjà connue et utilisée par plusieurs civilisations anciennes, plus de mille ans avant Pythagore.
Découvertes antérieures à Pythagore
Les Babyloniens de la période paléo-babylonienne (environ 1800 av. J.-C.) connaissaient déjà les triplets pythagoriciens. La célèbre tablette Plimpton 322, découverte au début du XIXe siècle, atteste de leur maîtrise de ces relations numériques. Les Égyptiens antiques utilisaient également ce principe, notamment à travers la fameuse corde à 13 nœuds, également appelée corde d’arpenteur ou corde égyptienne.
La corde à 13 nœuds : un outil géométrique ancestral
Cette corde comportait 13 nœuds régulièrement espacés, créant ainsi 12 intervalles égaux. Les arpenteurs et bâtisseurs égyptiens l’utilisaient pour tracer des angles droits sur le terrain. En formant un triangle avec des côtés mesurant respectivement 3, 4 et 5 intervalles (3 + 4 + 5 = 12), ils obtenaient automatiquement un angle droit, car ces nombres vérifient la relation pythagoricienne :
Cette technique pragmatique permettait de redéfinir les limites des champs après les crues du Nil, qui effaçaient régulièrement les frontières agricoles. Les bâtisseurs du Moyen Âge auraient également utilisé cet outil pour assurer la perpendicularité des murs lors de la construction des cathédrales.
L’apport de Pythagore et de son école
Pythagore, fondateur de l’école pythagoricienne à Crotone (Italie du Sud), n’a probablement pas découvert cette relation, mais il aurait été le premier à en fournir une démonstration mathématique rigoureuse et à en établir la formule générale. Les pythagoriciens voyaient dans les nombres l’essence même de l’harmonie universelle, et ce théorème incarnait parfaitement cette vision philosophique.
La plus ancienne démonstration complète qui nous soit parvenue figure dans les Éléments d’Euclide (vers 300 av. J.-C.), où elle apparaît comme la proposition I.47, considérée comme l’une des plus élégantes de tout l’ouvrage.
Démonstration du théorème de Pythagore
Il existe plus de 370 démonstrations différentes du théorème de Pythagore, ce qui témoigne de sa richesse mathématique et de son importance historique. Nous présentons ici deux démonstrations accessibles et visuellement parlantes.
Démonstration par aires (méthode d’Euclide simplifiée)
Cette démonstration repose sur la comparaison des aires de carrés construits sur les côtés du triangle rectangle. L’idée centrale est que l’aire du carré construit sur l’hypoténuse égale la somme des aires des carrés construits sur les deux cathètes.
Principe : On construit trois carrés, un sur chaque côté du triangle rectangle. Si les côtés du triangle mesurent \( a \), \( b \) et \( c \) (où \( c \) est l’hypoténuse), alors :
Ce qui se traduit directement par : \( c^2 = a^2 + b^2 \)
Réciproque du théorème de Pythagore
La réciproque du théorème de Pythagore est tout aussi importante que le théorème lui-même. Elle permet de déterminer si un triangle est rectangle uniquement à partir des longueurs de ses trois côtés, sans avoir à mesurer les angles.
Réciproque du théorème de Pythagore : Si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et le plus grand côté est son hypoténuse.
Mathématiquement, pour un triangle ABC avec BC comme plus grand côté :
Contraposée du théorème
Il existe également une contraposée utile pour prouver qu’un triangle n’est pas rectangle :
Contraposée : Si dans un triangle, le carré de la longueur du plus grand côté n’est pas égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle n’est pas rectangle.
Méthode d’application de la réciproque
Pour vérifier si un triangle est rectangle à l’aide de la réciproque, suivez cette démarche méthodique :
- Identifier le côté le plus long du triangle (l’hypoténuse potentielle)
- Calculer le carré de sa longueur
- Calculer la somme des carrés des deux autres côtés
- Comparer les deux résultats :
- S’ils sont égaux : le triangle est rectangle
- S’ils sont différents : le triangle n’est pas rectangle
- Conclure en citant la réciproque (ou la contraposée) du théorème de Pythagore
Attention : Une erreur fréquente consiste à ne pas identifier correctement le plus grand côté. Il est impératif de comparer le carré du plus grand côté avec la somme des carrés des deux autres, et non l’inverse. Cette rigueur est essentielle pour une application correcte de la réciproque.
Les triplets pythagoriciens
Un triplet pythagoricien est un ensemble de trois nombres entiers naturels \( (a, b, c) \) qui vérifient la relation de Pythagore :
Ces triplets sont particulièrement intéressants car ils permettent de construire des triangles rectangles dont tous les côtés ont des longueurs entières.
Exemples de triplets pythagoriciens
| Cathète a | Cathète b | Hypoténuse c | Vérification |
|---|---|---|---|
| 3 | 4 | 5 | \( 3^2 + 4^2 = 9 + 16 = 25 = 5^2 \) |
| 5 | 12 | 13 | \( 5^2 + 12^2 = 25 + 144 = 169 = 13^2 \) |
| 8 | 15 | 17 | \( 8^2 + 15^2 = 64 + 225 = 289 = 17^2 \) |
| 7 | 24 | 25 | \( 7^2 + 24^2 = 49 + 576 = 625 = 25^2 \) |
| 20 | 21 | 29 | \( 20^2 + 21^2 = 400 + 441 = 841 = 29^2 \) |
Triplets pythagoriciens primitifs
Un triplet pythagoricien est dit primitif si les trois nombres sont premiers entre eux (leur PGCD vaut 1). Le triplet (3, 4, 5) est primitif, tandis que (6, 8, 10) ne l’est pas car c’est simplement le double de (3, 4, 5).
Il existe une formule générale pour générer tous les triplets pythagoriciens primitifs à partir de deux entiers \( p \) et \( q \) tels que \( p > q > 0 \) :
a &= p^2 – q^2 \\
b &= 2pq \\
c &= p^2 + q^2
\end{align*}
Par exemple, avec \( p = 2 \) et \( q = 1 \), on obtient le triplet (3, 4, 5).
Applications du théorème de Pythagore
Le théorème de Pythagore trouve des applications dans de nombreux domaines scientifiques et techniques. Voici quelques exemples concrets qui illustrent son utilité pratique.
Calcul de distances en géométrie plane
Dans un repère orthonormé du plan, la distance entre deux points \( A(x_A, y_A) \) et \( B(x_B, y_B) \) se calcule grâce au théorème de Pythagore :
Cette formule découle directement du théorème appliqué au triangle rectangle formé par la projection des points sur les axes.
Architecture et construction
Les architectes et maçons utilisent quotidiennement le théorème de Pythagore pour vérifier l’équerrage des structures. La méthode ancestrale du 3-4-5 (ou sa version moderne 60 cm – 80 cm – 100 cm) permet de contrôler rapidement la perpendicularité de deux murs sans équerre sophistiquée.
Navigation et cartographie
En navigation maritime ou aérienne, le théorème permet de calculer la distance directe entre deux points lorsqu’on connaît leurs coordonnées géographiques projetées. Les systèmes GPS utilisent une généralisation tridimensionnelle de ce principe.
Trigonométrie : identité fondamentale
Le cercle trigonométrique de rayon 1 illustre une application remarquable du théorème. Pour tout angle \( \alpha \), les coordonnées du point correspondant sont \( (\cos\alpha, \sin\alpha) \). Comme ce point est à distance 1 de l’origine, on obtient l’identité trigonométrique fondamentale :
Cette relation, conséquence directe du théorème de Pythagore, est au cœur de toute la trigonométrie.
Exercices corrigés sur le théorème de Pythagore
La maîtrise du théorème de Pythagore s’acquiert par la pratique. Voici une série d’exercices progressifs avec leurs solutions détaillées.
Exercice 1 : Calcul de l’hypoténuse d’un triangle rectangle
Facile
Un triangle ABC est rectangle en A. On connaît les longueurs des deux cathètes :
- AB = 6 cm
- AC = 8 cm
- Identifier l’hypoténuse du triangle.
- Calculer la longueur BC.
- Reconnaître s’il s’agit d’un triplet pythagoricien.
Indication
L’hypoténuse est le côté opposé à l’angle droit. Utilisez la formule \( c^2 = a^2 + b^2 \) où c représente l’hypoténuse.
Voir le corrigé
Le triangle ABC est rectangle en A, donc l’angle droit est situé au sommet A. L’hypoténuse est le côté opposé à cet angle, c’est-à-dire BC.
Solution de la question 2 :
D’après le théorème de Pythagore :
BC^2 &= AB^2 + AC^2 \\
BC^2 &= 6^2 + 8^2 \\
BC^2 &= 36 + 64 \\
BC^2 &= 100 \\
BC &= \sqrt{100} \\
BC &= 10 \text{ cm}
\end{align*}
Solution de la question 3 :
Les longueurs (6, 8, 10) forment un triplet pythagoricien. Il s’agit du double du triplet primitif (3, 4, 5), l’un des plus célèbres triplets pythagoriciens.
Réponse finale : La longueur de l’hypoténuse BC est de 10 cm.
Exercice 2 : Application de la réciproque du théorème
Moyen
Un triangle GHI possède les dimensions suivantes :
- GH = 7 cm
- HI = 24 cm
- GI = 25 cm
- Identifier le plus grand côté du triangle.
- Vérifier si l’égalité de Pythagore est satisfaite.
- Conclure sur la nature du triangle et préciser l’angle droit s’il existe.
Indication
Pour appliquer la réciproque, comparez \( c^2 \) (carré du plus grand côté) avec \( a^2 + b^2 \) (somme des carrés des deux autres côtés). Si l’égalité est vérifiée, le triangle est rectangle.
Voir le corrigé
En comparant les trois longueurs, le plus grand côté est GI avec 25 cm. C’est donc l’hypoténuse potentielle.
Solution de la question 2 :
Calculons séparément les deux membres de l’égalité :
\text{D’une part : } GI^2 &= 25^2 = 625 \\
\text{D’autre part : } GH^2 + HI^2 &= 7^2 + 24^2 \\
&= 49 + 576 \\
&= 625
\end{align*}
Nous constatons que \( GI^2 = GH^2 + HI^2 \). L’égalité de Pythagore est vérifiée.
Solution de la question 3 :
D’après la réciproque du théorème de Pythagore, puisque le carré du plus grand côté égale la somme des carrés des deux autres côtés, le triangle GHI est rectangle. L’angle droit se situe au sommet opposé à l’hypoténuse, c’est-à-dire en H.
Conclusion : Le triangle GHI est rectangle en H. On reconnaît le triplet pythagoricien (7, 24, 25).
Exercice 3 : Distance entre deux points dans un repère
Moyen
Dans un repère orthonormé \( (O; \vec{i}, \vec{j}) \), on considère les points :
- M(2, 3)
- N(6, 6)
- Expliquer comment le théorème de Pythagore intervient dans le calcul de la distance MN.
- Calculer la distance MN.
Indication
La formule de distance \( d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} \) découle directement du théorème de Pythagore appliqué au triangle rectangle formé par les projections des points sur les axes.
Voir le corrigé
Pour calculer la distance entre M et N, on forme un triangle rectangle dont :
- L’hypoténuse est le segment [MN]
- Une cathète mesure la différence des abscisses : \( |x_N – x_M| = |6 – 2| = 4 \)
- L’autre cathète mesure la différence des ordonnées : \( |y_N – y_M| = |6 – 3| = 3 \)
Le théorème de Pythagore permet alors de calculer MN.
Solution de la question 2 :
Application de la formule de distance :
MN &= \sqrt{(x_N – x_M)^2 + (y_N – y_M)^2} \\
MN &= \sqrt{(6 – 2)^2 + (6 – 3)^2} \\
MN &= \sqrt{4^2 + 3^2} \\
MN &= \sqrt{16 + 9} \\
MN &= \sqrt{25} \\
MN &= 5 \text{ unités}
\end{align*}
Réponse finale : La distance entre les points M et N est de 5 unités de longueur. On retrouve encore le triplet (3, 4, 5).
Exercice 4 : Problème de diagonale d’un rectangle
Difficile
Un rectangle ABCD a pour dimensions :
- Longueur AB = 12 cm
- Largeur BC = 5 cm
- Expliquer pourquoi le triangle ABC est rectangle.
- Calculer la longueur de la diagonale AC.
- Que peut-on dire de la diagonale BD ? Justifier.
Indication
Dans un rectangle, tous les angles sont droits. Les diagonales d’un rectangle ont la même longueur et se coupent en leur milieu.
Voir le corrigé
ABCD est un rectangle, donc tous ses angles sont droits. En particulier, l’angle en B est un angle droit, ce qui signifie que le triangle ABC est rectangle en B.
Solution de la question 2 :
Dans le triangle ABC rectangle en B, AC est l’hypoténuse. D’après le théorème de Pythagore :
AC^2 &= AB^2 + BC^2 \\
AC^2 &= 12^2 + 5^2 \\
AC^2 &= 144 + 25 \\
AC^2 &= 169 \\
AC &= \sqrt{169} \\
AC &= 13 \text{ cm}
\end{align*}
Solution de la question 3 :
Dans un rectangle, les deux diagonales ont la même longueur. Par conséquent, BD = AC = 13 cm. On retrouve le triplet pythagoricien (5, 12, 13).
Réponse finale : La diagonale AC mesure 13 cm, et la diagonale BD mesure également 13 cm.
Erreurs fréquentes à éviter
Les pièges classiques
1. Confusion entre théorème et réciproque
- Le théorème permet de calculer un côté d’un triangle déjà connu comme rectangle
- La réciproque permet de démontrer qu’un triangle est rectangle
2. Oubli de la racine carrée
Après avoir calculé \( c^2 \), il faut impérativement extraire la racine carrée pour obtenir \( c \). Par exemple, si \( c^2 = 25 \), alors \( c = 5 \) (et non 25).
3. Mauvaise identification de l’hypoténuse
L’hypoténuse est toujours le côté le plus long, celui opposé à l’angle droit. Ne jamais appliquer la formule \( a^2 + b^2 = c^2 \) si \( c \) n’est pas le plus grand côté.
4. Application à des triangles non rectangles
Le théorème de Pythagore ne s’applique qu’aux triangles rectangles. Vérifiez toujours la présence d’un angle droit avant de l’utiliser.
5. Erreurs de calcul
Soyez rigoureux dans les opérations : \( (a + b)^2 \neq a^2 + b^2 \). Le carré d’une somme n’est pas la somme des carrés.
Synthèse et points clés
Résumons les éléments essentiels à retenir sur le théorème de Pythagore :
- Théorème direct : Dans un triangle rectangle, le carré de l’hypoténuse égale la somme des carrés des cathètes : \( c^2 = a^2 + b^2 \)
- Réciproque : Si l’égalité \( c^2 = a^2 + b^2 \) est vérifiée (où \( c \) est le plus grand côté), alors le triangle est rectangle
- Contraposée : Si \( c^2 \neq a^2 + b^2 \), alors le triangle n’est pas rectangle
- Triplets pythagoriciens : Ensembles d’entiers vérifiant la relation (ex : 3-4-5, 5-12-13, 8-15-17)
- Applications : Calcul de distances, vérification d’angles droits, trigonométrie, architecture
- Histoire : Connu depuis l’Antiquité (Babyloniens, Égyptiens), formalisé par Pythagore, démontré rigoureusement par Euclide
La maîtrise de ce théorème est fondamentale pour progresser en géométrie et aborder sereinement des notions plus avancées comme la trigonométrie, la géométrie analytique ou encore le calcul vectoriel.
Questions fréquemment posées (FAQ)
Quelle est la différence entre le théorème de Pythagore et sa réciproque ?
Le théorème de Pythagore s’utilise lorsque l’on sait déjà que le triangle est rectangle et permet de calculer la longueur d’un côté à partir des deux autres. La réciproque, quant à elle, permet de déterminer si un triangle est rectangle en vérifiant si la relation \( c^2 = a^2 + b^2 \) est satisfaite pour le plus grand côté.
Comment identifier l’hypoténuse dans un triangle rectangle ?
L’hypoténuse est toujours le côté le plus long d’un triangle rectangle. C’est également le côté qui est opposé à l’angle droit. Si vous placez l’angle droit face à vous, l’hypoténuse est le côté qui vous fait face, en diagonale par rapport aux deux autres côtés qui forment l’angle droit.
Qu’est-ce qu’un triplet pythagoricien ?
Un triplet pythagoricien est un ensemble de trois nombres entiers naturels \( (a, b, c) \) qui vérifient la relation \( a^2 + b^2 = c^2 \). Les exemples les plus célèbres sont (3, 4, 5), (5, 12, 13) et (8, 15, 17). Ces triplets permettent de construire des triangles rectangles dont tous les côtés ont des longueurs entières.
Peut-on utiliser le théorème de Pythagore pour n’importe quel triangle ?
Non, le théorème de Pythagore s’applique uniquement aux triangles rectangles. Pour les triangles quelconques, on utilise d’autres formules comme le théorème d’Al-Kashi (ou loi des cosinus) qui généralise le théorème de Pythagore : \( c^2 = a^2 + b^2 – 2ab\cos(C) \).
Quelle est la relation entre le théorème de Pythagore et la trigonométrie ?
Le théorème de Pythagore est à l’origine de l’identité trigonométrique fondamentale \( \cos^2\alpha + \sin^2\alpha = 1 \). Cette relation découle de l’application du théorème au triangle rectangle inscrit dans le cercle trigonométrique de rayon 1, où les coordonnées du point sont \( (\cos\alpha, \sin\alpha) \).