Définition et notation de la probabilité conditionnelle
Définition
On appelle probabilité conditionnelle de B sachant A, la probabilité que l’événement \( B \) se réalise sachant que l’événement \( A \) est réalisé.
Notation : \( P_A(B) \) ou \( P(B|A) \)
On lit : « probabilité de B sachant A »
Interprétation intuitive : Quand on calcule \( P_A(B) \), on se place dans un nouvel univers restreint où l’événement \( A \) est déjà réalisé. On cherche alors quelle est la probabilité que \( B \) se produise dans cet univers réduit.
Propriété importante : Comme toute probabilité, on a toujours :
\[ 0 \leq P_A(B) \leq 1 \]
Calculer avec un tableau à double entrée
Lorsque les données sont présentées dans un tableau à double entrée, le calcul des probabilités conditionnelles devient très intuitif.
Exemple : Étude pharmaceutique
Un laboratoire teste deux médicaments sur 800 patients atteints d’une maladie. Voici les résultats :
| Médicament A | Médicament B | Total | |
|---|---|---|---|
| Guéri | 383 | 291 | 674 |
| Non guéri | 72 | 54 | 126 |
| Total | 455 | 345 | 800 |
On note les événements :
- \( A \) : « Le patient a pris le médicament A »
- \( G \) : « Le patient est guéri »
Calculs des probabilités simples :
\[ P(A) = \frac{455}{800} \approx 0{,}57 = 57\,\% \]
\[ P(G) = \frac{674}{800} \approx 0{,}84 = 84\,\% \]
\[ P(G \cap A) = \frac{383}{800} \approx 0{,}48 = 48\,\% \]
Calcul de probabilité conditionnelle avec le tableau :
Question : On choisit au hasard un patient guéri. Quelle est la probabilité qu’il ait pris le médicament A ?
Méthode : On se restreint à la ligne des patients guéris (674 patients). Parmi eux, 383 ont pris le médicament A.
\[ P_G(A) = \frac{383}{674} \approx 0{,}57 = 57\,\% \]
Autre question : On choisit un patient ayant pris le médicament B. Quelle est la probabilité qu’il soit guéri ?
On se restreint à la colonne du médicament B (345 patients). Parmi eux, 291 sont guéris.
\[ P_B(G) = \frac{291}{345} \approx 0{,}84 = 84\,\% \]
La formule fondamentale
Lorsque les données ne sont pas présentées sous forme de tableau, on utilise la formule de définition des probabilités conditionnelles.
Formule fondamentale
Soient \( A \) et \( B \) deux événements avec \( P(A) \neq 0 \). La probabilité conditionnelle de \( B \) sachant \( A \) est :
\[ P_A(B) = \frac{P(A \cap B)}{P(A)} \]
Interprétation : Cette formule exprime que pour calculer \( P_A(B) \), on divise la probabilité que \( A \) et \( B \) se réalisent ensemble par la probabilité que \( A \) se réalise.
Formule équivalente (formule du produit) :
En réarrangeant la formule précédente, on obtient une relation très utile :
\[ P(A \cap B) = P(A) \times P_A(B) \]
Cette formule signifie que la probabilité que deux événements se produisent ensemble est égale à la probabilité du premier multiplié par la probabilité conditionnelle du second sachant le premier.
Exemple d’application :
Énoncé : On tire une carte au hasard dans un jeu de 32 cartes.
- \( A \) : « La carte est un pique »
- \( B \) : « La carte est un roi »
Question : Calculer \( P_A(B) \), la probabilité que la carte soit un roi sachant qu’elle est un pique.
Solution :
\begin{align*}
P(A) &= \frac{8}{32} = \frac{1}{4} \\
P(A \cap B) &= \frac{1}{32} \quad \text{(il n’y a qu’un seul roi de pique)} \\
P_A(B) &= \frac{P(A \cap B)}{P(A)} = \frac{\frac{1}{32}}{\frac{1}{4}} = \frac{1}{32} \times \frac{4}{1} = \frac{1}{8}
\end{align*}
Vérification intuitive : Parmi les 8 piques, il y a 1 seul roi. Donc la probabilité est bien \( \frac{1}{8} \).
Propriété complémentaire :
\[ P_A(\overline{B}) = 1 – P_A(B) \]
Cette propriété est analogue à celle des probabilités simples : la somme des probabilités conditionnelles d’un événement et de son contraire vaut 1.
Arbres pondérés et probabilités conditionnelles
Les arbres pondérés (ou arbres de probabilités) sont des outils visuels puissants pour représenter et calculer les probabilités conditionnelles dans les expériences à plusieurs étapes.
Structure d’un arbre pondéré :
- Au premier niveau, on place les probabilités des événements initiaux
- Au deuxième niveau, on place les probabilités conditionnelles sachant les événements du premier niveau
- Chaque branche représente un événement possible
- Chaque chemin (suite de branches) représente une intersection d’événements
Les trois règles fondamentales des arbres pondérés :
Règle 1 : Somme au nœud
À partir d’un même nœud, la somme des probabilités des branches qui en partent est égale à 1.
Règle 2 : Produit le long d’un chemin
Pour calculer la probabilité d’un chemin, on multiplie les probabilités des branches de ce chemin.
\[ P(A \cap B) = P(A) \times P_A(B) \]
Règle 3 : Somme des chemins (Probabilités totales)
La probabilité d’un événement associé à plusieurs chemins est égale à la somme des probabilités de chacun de ces chemins.
Exemple complet : L’urne aux boules marquées
Situation : Une urne contient 50 boules :
- 20 boules rouges dont 15 marquées « Gagné »
- 30 boules noires dont 9 marquées « Gagné »
On tire une boule au hasard. On note :
- \( R \) : « Tirer une boule rouge »
- \( G \) : « Tirer une boule marquée Gagné »
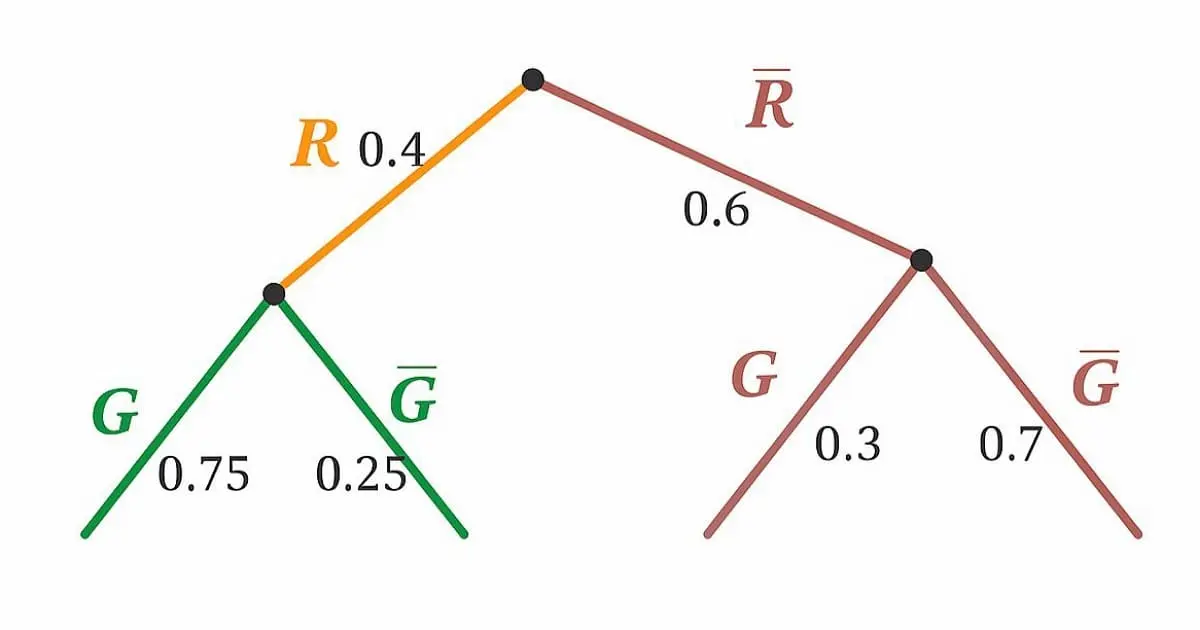
Calculs étape par étape :
a) Probabilité initiale :
\[ P(R) = \frac{20}{50} = 0{,}4 \]
Donc \( P(\overline{R}) = 1 – 0{,}4 = 0{,}6 \) (Règle 1)
b) Probabilités conditionnelles :
\begin{align*}
P_R(G) &= \frac{15}{20} = 0{,}75 \\
P_{\overline{R}}(G) &= \frac{9}{30} = 0{,}3
\end{align*}
c) Probabilités d’intersection (Règle 2) :
\begin{align*}
P(R \cap G) &= P(R) \times P_R(G) = 0{,}4 \times 0{,}75 = 0{,}3 \\
P(\overline{R} \cap G) &= P(\overline{R}) \times P_{\overline{R}}(G) = 0{,}6 \times 0{,}3 = 0{,}18
\end{align*}
d) Probabilité totale de gagner (Règle 3) :
\[ P(G) = P(R \cap G) + P(\overline{R} \cap G) = 0{,}3 + 0{,}18 = 0{,}48 = 48\,\% \]
Formule des probabilités totales
La formule des probabilités totales est un outil essentiel pour calculer la probabilité d’un événement lorsque l’univers est divisé en plusieurs cas mutuellement exclusifs.
Théorème : Formule des probabilités totales
Soit \( A_1, A_2, \ldots, A_n \) des événements qui forment une partition de l’univers \( \Omega \) (c’est-à-dire qu’ils sont deux à deux incompatibles et que leur réunion est \( \Omega \)).
Pour tout événement \( B \), on a :
\[ P(B) = P(A_1 \cap B) + P(A_2 \cap B) + \cdots + P(A_n \cap B) \]
Ou, en utilisant les probabilités conditionnelles :
\[ P(B) = P(A_1) \times P_{A_1}(B) + P(A_2) \times P_{A_2}(B) + \cdots + P(A_n) \times P_{A_n}(B) \]
Cas particulier important (partition à deux événements) :
Quand la partition est formée d’un événement \( A \) et de son contraire \( \overline{A} \) :
\[ P(B) = P(A) \times P_A(B) + P(\overline{A}) \times P_{\overline{A}}(B) \]
Application pratique : Test de dépistage
Contexte : Lors d’une épidémie chez les bovins, un test de dépistage est mis au point. Sur un échantillon :
- 2% des animaux sont porteurs de la maladie
- Si un animal est malade, le test est positif dans 85% des cas
- Si un animal est sain, le test est négatif dans 95% des cas
On note :
- \( M \) : « L’animal est malade »
- \( T \) : « Le test est positif »
Question : Quelle est la probabilité qu’un animal choisi au hasard ait un test positif ?
Solution :
D’après les données :
- \( P(M) = 0{,}02 \) donc \( P(\overline{M}) = 0{,}98 \)
- \( P_M(T) = 0{,}85 \) (sensibilité du test)
- \( P_{\overline{M}}(\overline{T}) = 0{,}95 \) donc \( P_{\overline{M}}(T) = 0{,}05 \) (1 – spécificité)
Application de la formule des probabilités totales :
\begin{align*}
P(T) &= P(M \cap T) + P(\overline{M} \cap T) \\
&= P(M) \times P_M(T) + P(\overline{M}) \times P_{\overline{M}}(T) \\
&= 0{,}02 \times 0{,}85 + 0{,}98 \times 0{,}05 \\
&= 0{,}017 + 0{,}049 \\
&= 0{,}066 = 6{,}6\,\%
\end{align*}
Conclusion : La probabilité qu’un animal ait un test positif est de 6,6%.
Théorème de Bayes : la probabilité des causes
Le théorème de Bayes, nommé d’après le révérend Thomas Bayes (18e siècle), est l’un des résultats les plus importants en probabilités. Il permet de calculer une probabilité conditionnelle « inverse », c’est-à-dire de remonter de l’effet à la cause.
Théorème de Bayes (version simple)
Soient \( A \) et \( B \) deux événements de probabilités non nulles. Alors :
\[ P_B(A) = \frac{P(A \cap B)}{P(B)} = \frac{P(A) \times P_A(B)}{P(B)} \]
Théorème de Bayes (version complète avec probabilités totales)
Si \( A \) et \( \overline{A} \) forment une partition de l’univers, alors :
\[ P_B(A) = \frac{P(A) \times P_A(B)}{P(A) \times P_A(B) + P(\overline{A}) \times P_{\overline{A}}(B)} \]
Interprétation : Cette formule permet de calculer la probabilité qu’un événement \( A \) soit la cause, sachant qu’on observe l’effet \( B \).
Application au test de dépistage (suite)
Reprenons l’exemple précédent du test de dépistage chez les bovins.
Nouvelle question : Si le test d’un bovin est positif, quelle est la probabilité qu’il soit réellement malade ?
On cherche \( P_T(M) \), c’est-à-dire la probabilité d’être malade sachant que le test est positif.
Solution avec Bayes :
\begin{align*}
P_T(M) &= \frac{P(M \cap T)}{P(T)} \\
&= \frac{0{,}02 \times 0{,}85}{0{,}066} \\
&= \frac{0{,}017}{0{,}066} \\
&\approx 0{,}26 = 26\,\%
\end{align*}
Conclusion surprenante : Même si le test est positif, la probabilité que l’animal soit réellement malade n’est que de 26% ! Cela s’explique par la faible prévalence de la maladie (2%) et le taux de faux positifs (5% des animaux sains).
Ce résultat contre-intuitif illustre l’importance du théorème de Bayes en médecine pour interpréter correctement les tests diagnostiques.
Événements indépendants
Définition d’événements indépendants
On dit que deux événements \( A \) et \( B \) sont indépendants lorsque la réalisation de l’un n’influence pas la probabilité de réalisation de l’autre.
Définition mathématique : Deux événements \( A \) et \( B \) sont indépendants si et seulement si :
\[ P(A \cap B) = P(A) \times P(B) \]
Propriété équivalente :
Deux événements \( A \) et \( B \) sont indépendants si et seulement si :
\[ P_A(B) = P(B) \quad \text{ou} \quad P_B(A) = P(A) \]
Autrement dit, connaître l’événement \( A \) ne change pas la probabilité de \( B \).
Exemple 1 : Démontrer l’indépendance
Situation : On tire une carte au hasard dans un jeu de 32 cartes.
- \( R \) : « On tire un roi »
- \( T \) : « On tire un trèfle »
Question : Les événements \( R \) et \( T \) sont-ils indépendants ?
Solution :
\begin{align*}
P(R) &= \frac{4}{32} = \frac{1}{8} \\
P(T) &= \frac{8}{32} = \frac{1}{4} \\
P(R \cap T) &= \frac{1}{32} \quad \text{(un seul roi de trèfle)} \\
P(R) \times P(T) &= \frac{1}{8} \times \frac{1}{4} = \frac{1}{32}
\end{align*}
Comme \( P(R \cap T) = P(R) \times P(T) \), les événements \( R \) et \( T \) sont indépendants.
Exemple 2 : Utiliser l’indépendance
Situation : Dans une population :
- Un individu a la maladie m avec probabilité 0,005
- Un individu a la maladie n avec probabilité 0,01
- Les maladies sont indépendantes
Question : Quelle est la probabilité qu’un individu ait au moins une des deux maladies ?
Solution :
Notons \( M \) : « avoir la maladie m » et \( N \) : « avoir la maladie n »
On cherche \( P(M \cup N) \). D’après la formule :
\begin{align*}
P(M \cup N) &= P(M) + P(N) – P(M \cap N) \\
&= P(M) + P(N) – P(M) \times P(N) \quad \text{(indépendance)} \\
&= 0{,}005 + 0{,}01 – 0{,}005 \times 0{,}01 \\
&= 0{,}015 – 0{,}00005 \\
&= 0{,}01495 = 1{,}495\,\%
\end{align*}
Propriété importante :
Si \( A \) et \( B \) sont indépendants, alors :
- \( \overline{A} \) et \( B \) sont indépendants
- \( A \) et \( \overline{B} \) sont indépendants
- \( \overline{A} \) et \( \overline{B} \) sont indépendants
Conclusion
Les probabilités conditionnelles constituent un concept fondamental en mathématiques et dans de nombreuses applications pratiques. Vous avez maintenant maîtrisé :
- La définition et la notation de la probabilité conditionnelle
- Les méthodes de calcul avec tableaux à double entrée et formules
- L’utilisation des arbres pondérés pour visualiser et calculer
- La formule des probabilités totales pour les situations complexes
- Le théorème de Bayes pour inverser les conditionnements
- La notion d’indépendance et ses applications
Ces outils sont essentiels pour résoudre des problèmes concrets en statistique, en médecine (fiabilité des tests diagnostiques), en informatique (intelligence artificielle, apprentissage automatique), en économie (prévisions), et dans de nombreux autres domaines.
Pour progresser : Entraînez-vous régulièrement avec des exercices variés, identifiez bien le type de situation (avec/sans remise, indépendance ou non), et n’hésitez pas à dessiner des arbres pondérés pour visualiser les problèmes complexes. La pratique régulière transformera ces formules en réflexes naturels.
Bon courage dans votre apprentissage des probabilités conditionnelles !
Questions fréquentes (FAQ)
Comment calculer une probabilité conditionnelle ?
Pour calculer une probabilité conditionnelle P_A(B), on utilise la formule P_A(B) = P(A ∩ B) / P(A). On peut aussi utiliser un arbre pondéré ou un tableau à double entrée selon les données disponibles. Dans un tableau, on se restreint à la ligne ou colonne correspondant à l’événement conditionné (A), puis on divise l’effectif de l’intersection par l’effectif total de A.
Quelle est la différence entre P(A∩B) et P_A(B) ?
P(A∩B) représente la probabilité que les événements A et B se réalisent simultanément dans l’univers complet. P_A(B) est la probabilité que B se réalise sachant que A est déjà réalisé, donc dans un univers restreint à A. La relation entre les deux est : P(A∩B) = P(A) × P_A(B).
Qu’est-ce que le théorème de Bayes ?
Le théorème de Bayes permet de calculer une probabilité conditionnelle inverse. La formule est P_B(A) = [P(A) × P_A(B)] / P(B). Il est particulièrement utile pour calculer la probabilité d’une cause sachant l’effet, par exemple en médecine pour déterminer la probabilité d’être malade sachant qu’un test est positif.
Comment utiliser un arbre pondéré en probabilité ?
Dans un arbre pondéré, suivez trois règles : (1) À partir d’un même nœud, la somme des probabilités vaut 1. (2) Pour calculer la probabilité d’un chemin, on multiplie les probabilités des branches. (3) La probabilité d’un événement associé à plusieurs chemins s’obtient en additionnant les probabilités de tous ces chemins. Au premier niveau, on place les probabilités simples ; au deuxième niveau, les probabilités conditionnelles.
Quand dit-on que deux événements sont indépendants ?
Deux événements A et B sont indépendants lorsque la réalisation de l’un n’influence pas la probabilité de l’autre. Mathématiquement, cela signifie que P(A∩B) = P(A) × P(B), ou de manière équivalente P_A(B) = P(B). Par exemple, lors de tirages avec remise, les résultats successifs sont indépendants car remettre la boule dans l’urne restaure les probabilités initiales.
Qu’est-ce que la formule des probabilités totales ?
La formule des probabilités totales permet de calculer la probabilité d’un événement B lorsque l’univers est divisé en plusieurs cas (partition). Si A₁, A₂, …, Aₙ forment une partition, alors P(B) = P(A₁)×P_A₁(B) + P(A₂)×P_A₂(B) + … + P(Aₙ)×P_Aₙ(B). Dans un arbre pondéré, cela correspond à additionner les probabilités de tous les chemins menant à B.
Comment distinguer tirage avec et sans remise ?
Dans un tirage avec remise, l’objet tiré est remis avant le tirage suivant, donc les probabilités restent identiques à chaque tirage et les événements sont indépendants. Dans un tirage sans remise, l’objet n’est pas remis, donc les probabilités changent au second tirage selon ce qui a été tiré en premier : on utilise alors des probabilités conditionnelles qui dépendent du résultat du premier tirage.