Imaginez un nombre si fascinant qu’il apparaît dans les pétales d’une fleur, les spirales d’un coquillage, les proportions du Parthénon et même dans les œuvres de Léonard de Vinci. Ce nombre mystérieux, appelé nombre d’or et noté par la lettre grecque φ (phi), vaut approximativement 1,618. Depuis l’Antiquité grecque, cette constante mathématique intrigue philosophes, artistes et scientifiques par son omniprésence dans la nature et son esthétique particulière.
Le nombre d’or représente un rapport de proportions considéré comme harmonieux. Lorsqu’un segment est divisé selon cette proportion, le rapport entre la grande partie et la petite partie est égal au rapport entre le tout et la grande partie. Cette propriété unique en fait un objet mathématique exceptionnel avec des applications concrètes en géométrie, en art, en architecture et même en finance.
Dans cette leçon complète, nous explorerons la définition rigoureuse du nombre d’or, sa formule exacte, ses propriétés algébriques remarquables, son lien profond avec la suite de Fibonacci, et ses manifestations dans le monde réel. Vous découvrirez également comment construire un rectangle d’or et résoudre des exercices pratiques.
Définition mathématique du nombre d’or
Définition par la proportion
Le nombre d’or, noté φ (phi), est le nombre réel positif qui satisfait l’égalité suivante : un segment de longueur \(a + b\) est divisé en deux parties \(a\) et \(b\) (avec \(a > b > 0\)) de telle sorte que le rapport de la longueur totale à la grande partie soit égal au rapport de la grande partie à la petite partie.
Formule exacte du nombre d’or
Pour déterminer la valeur exacte de φ, posons \(x = \frac{a}{b}\). D’après la définition, nous avons :
En développant cette équation, nous obtenons :
x + 1 &= x^2 \\
x^2 – x – 1 &= 0
\end{align*}
Cette équation du second degré admet deux solutions. En utilisant la formule quadratique avec \(a=1\), \(b=-1\), \(c=-1\) :
\Delta &= (-1)^2 – 4(1)(-1) = 1 + 4 = 5 \\
x &= \frac{1 \pm \sqrt{5}}{2}
\end{align*}
Puisque φ est un nombre positif (rapport de longueurs positives), nous retenons uniquement la solution positive :
La solution négative \(\frac{1 – \sqrt{5}}{2} \approx -0{,}618\) est parfois notée \(\Phi\) (phi majuscule) ou \(-\frac{1}{\varphi}\), et possède également des propriétés intéressantes.
Propriétés algébriques remarquables
Le nombre d’or possède des propriétés mathématiques extraordinaires qui le distinguent des autres nombres irrationnels.
Propriété fondamentale
De l’équation \(\varphi^2 – \varphi – 1 = 0\), nous déduisons immédiatement :
Cette relation signifie que le carré du nombre d’or est égal au nombre d’or augmenté de 1.
Inverse du nombre d’or
Une propriété surprenante concerne l’inverse de φ. Divisons les deux membres de \(\varphi^2 = \varphi + 1\) par \(\varphi\) :
\varphi &= 1 + \frac{1}{\varphi} \\
\frac{1}{\varphi} &= \varphi – 1
\end{align*}
En substituant la valeur de φ :
L’inverse de φ est égal à sa partie décimale ! C’est une propriété unique parmi les nombres positifs.
Puissances du nombre d’or
La relation \(\varphi^2 = \varphi + 1\) permet de calculer facilement toutes les puissances de φ :
\varphi^3 &= \varphi \cdot \varphi^2 = \varphi(\varphi + 1) = \varphi^2 + \varphi = (\varphi+1) + \varphi = 2\varphi + 1 \\
\varphi^4 &= \varphi \cdot \varphi^3 = \varphi(2\varphi + 1) = 2\varphi^2 + \varphi = 2(\varphi+1) + \varphi = 3\varphi + 2 \\
\varphi^5 &= \varphi \cdot \varphi^4 = \varphi(3\varphi + 2) = 3\varphi^2 + 2\varphi = 3(\varphi+1) + 2\varphi = 5\varphi + 3
\end{align*}
On observe que les coefficients (1, 1, 2, 3, 5…) forment la célèbre suite de Fibonacci !
Lien entre le nombre d’or et la suite de Fibonacci
La suite de Fibonacci est une suite célèbre où chaque terme est la somme des deux précédents. Elle commence par \(F_0 = 0\) et \(F_1 = 1\), puis :
Les premiers termes sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Convergence du rapport de termes consécutifs
Un résultat remarquable lie cette suite au nombre d’or. Considérons le rapport de deux termes consécutifs :
Vérifions avec quelques valeurs :
| \(n\) | \(F_n\) | \(F_{n+1}\) | \(\frac{F_{n+1}}{F_n}\) |
|---|---|---|---|
| 5 | 5 | 8 | 1,600 |
| 10 | 55 | 89 | 1,618 181 818… |
| 15 | 610 | 987 | 1,618 032 786… |
| 20 | 6 765 | 10 946 | 1,618 033 988… |
Plus \(n\) augmente, plus le rapport se rapproche de φ ≈ 1,618 033 989.
Formule de Binet
Il existe une formule explicite donnant directement le \(n\)-ième terme de Fibonacci en fonction du nombre d’or :
où \(\Phi = \frac{1-\sqrt{5}}{2} = -\frac{1}{\varphi}\) est le conjugué du nombre d’or.
Cette formule relie explicitement la suite de Fibonacci, définie par récurrence, au nombre d’or défini algébriquement.
Constructions géométriques : rectangle d’or et spirale
Le rectangle d’or
Un rectangle d’or est un rectangle dont les côtés sont dans le rapport φ. Si la largeur est 1, la longueur est φ ≈ 1,618. Ce rectangle possède une propriété remarquable : si on lui enlève un carré, le rectangle restant est encore un rectangle d’or.
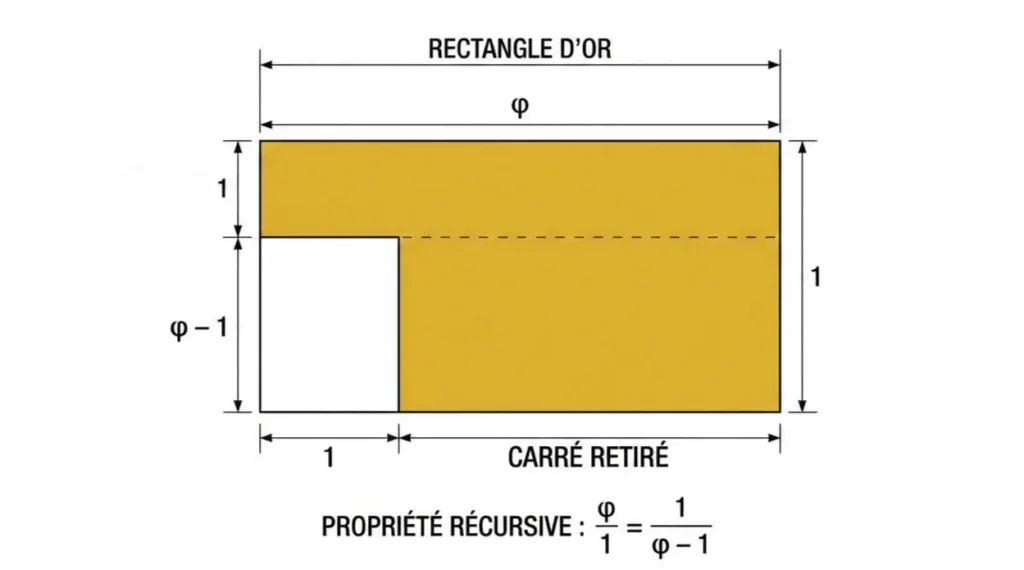
Construction à la règle et au compas
Voici comment construire un rectangle d’or :
- Tracer un carré ABCD de côté 1
- Marquer le milieu M du côté [AB]
- Tracer le segment [MC]
- La longueur MC vaut \(\frac{\sqrt{5}}{2}\) (théorème de Pythagore : \(MC = \sqrt{(\frac{1}{2})^2 + 1^2}\))
- Reporter cette longueur sur la droite (AB) prolongée au-delà de B pour obtenir le point E
- La longueur AE vaut \(\frac{1}{2} + \frac{\sqrt{5}}{2} = \frac{1+\sqrt{5}}{2} = \varphi\)
La spirale d’or
En répétant le processus de subdivision d’un rectangle d’or et en traçant des quarts de cercle dans chaque carré obtenu, on construit la célèbre spirale d’or (ou spirale de Fibonacci). Cette spirale approxime la spirale logarithmique et apparaît fréquemment dans la nature.
Applications du nombre d’or en architecture et dans la nature
Architecture et art
Le nombre d’or a été utilisé (consciemment ou non) dans de nombreuses œuvres architecturales et artistiques considérées comme particulièrement harmonieuses :
- Le Parthénon d’Athènes : Les dimensions de la façade s’inscrivent approximativement dans un rectangle d’or
- Les pyramides d’Égypte : Certains chercheurs ont identifié des proportions dorées dans les pyramides de Gizeh
- La Joconde de Léonard de Vinci : Le visage peut être encadré par des rectangles d’or
- Architecture moderne : Le Corbusier a développé le « Modulor », un système de proportions basé sur le nombre d’or et les dimensions humaines
Manifestations dans la nature
La nature regorge d’exemples où apparaissent le nombre d’or et la suite de Fibonacci :
- Phyllotaxie : L’arrangement des feuilles autour d’une tige, des écailles d’un ananas ou d’une pomme de pin suit souvent des nombres de Fibonacci
- Spirales de coquillages : Le nautile présente une spirale logarithmique proche de la spirale d’or
- Pétales de fleurs : De nombreuses fleurs ont un nombre de pétales correspondant à un terme de Fibonacci (3 pour le lys, 5 pour la rose sauvage, 8 pour la cosmea, 13 pour la marguerite, etc.)
- Proportions du corps humain : Certains rapports de segments du corps humain s’approchent de φ (phalange-main, avant-bras-bras, etc.)
Attention : Il faut rester critique face aux affirmations sur le nombre d’or. Toutes les observations dans la nature ou l’art ne correspondent pas exactement à φ, et certaines associations relèvent plus du mythe que de la réalité mesurable. Une différence de quelques pourcents avec φ ne constitue pas une véritable manifestation du nombre d’or.
Exercices corrigés sur le nombre d’or
Exercice 1 : Vérification algébrique
Énoncé : Démontrer que \(\varphi^3 = 2\varphi + 1\).
Solution :
\varphi^3 &= \varphi \times \varphi^2 \\
&= \varphi \times (\varphi + 1) \quad \text{(car } \varphi^2 = \varphi + 1\text{)} \\
&= \varphi^2 + \varphi \\
&= (\varphi + 1) + \varphi \quad \text{(en remplaçant à nouveau } \varphi^2\text{)} \\
&= 2\varphi + 1
\end{align*}
La propriété est démontrée.
Exercice 2 : Rectangle d’or
Énoncé : Un rectangle a pour dimensions 10 cm et 16,18 cm. Est-ce un rectangle d’or ?
Solution :
Pour qu’un rectangle soit un rectangle d’or, le rapport longueur/largeur doit être égal à φ.
Or, \(\varphi = \frac{1+\sqrt{5}}{2} \approx 1{,}618\,033\,989\).
Le rapport calculé (1,618) est très proche de φ mais pas exactement égal. À 0,002% près, on peut considérer que c’est approximativement un rectangle d’or, mais mathématiquement, ce n’en est pas un au sens strict.
Exercice 3 : Suite de Fibonacci
Énoncé : Calculer \(\frac{F_{12}}{F_{11}}\) sachant que \(F_{10} = 55\), \(F_{11} = 89\), et comparer à φ.
Solution :
D’abord, calculons \(F_{12}\) :
Ensuite, le rapport :
Comparaison avec \(\varphi \approx 1{,}618\,033\,989\) :
L’écart est d’environ 0,0035%. Le rapport converge bien vers le nombre d’or.
Exercice 4 : Équation avec φ
Énoncé : Résoudre l’équation \(x^2 = x + 1\) et retrouver le nombre d’or.
Solution :
Réécrivons l’équation sous forme standard :
Coefficients : \(a = 1\), \(b = -1\), \(c = -1\).
Discriminant :
Solutions :
Les deux solutions sont :
- \(x_1 = \frac{1 + \sqrt{5}}{2} = \varphi\) (le nombre d’or)
- \(x_2 = \frac{1 – \sqrt{5}}{2} \approx -0{,}618\) (le conjugué négatif)
Conclusion et synthèse
Le nombre d’or φ ≈ 1,618 est bien plus qu’une simple curiosité mathématique. C’est une constante qui émerge naturellement de contraintes géométriques simples et qui se manifeste dans des contextes extrêmement variés.
Points clés à retenir :
- Le nombre d’or est défini par la proportion \(\frac{a+b}{a} = \frac{a}{b} = \varphi\), ce qui conduit à la formule exacte \(\varphi = \frac{1+\sqrt{5}}{2}\)
- Il satisfait l’équation remarquable \(\varphi^2 = \varphi + 1\), d’où découlent toutes ses propriétés algébriques
- Son inverse égale sa partie décimale : \(\frac{1}{\varphi} = \varphi – 1 \approx 0{,}618\)
- Le rapport de deux termes consécutifs de la suite de Fibonacci converge vers φ
- Il apparaît dans des constructions géométriques (rectangle d’or, spirale d’or) et dans la nature (phyllotaxie, coquillages)
- Il a inspiré architectes et artistes à travers l’histoire, même si toutes les affirmations à son sujet ne sont pas scientifiquement vérifiées
Le nombre d’or continue de fasciner par son élégance mathématique et son omniprésence apparente. Son étude constitue un excellent exemple de la façon dont les mathématiques pures peuvent éclairer des phénomènes naturels et esthétiques.
Questions fréquemment posées
Quelle est la formule du nombre d’or ?
La formule exacte du nombre d’or est \(\varphi = \frac{1 + \sqrt{5}}{2}\), ce qui donne approximativement 1,618 033 989. Cette formule provient de la résolution de l’équation \(x^2 – x – 1 = 0\), qui traduit mathématiquement la proportion dorée.
Quel est le lien entre Fibonacci et le nombre d’or ?
Le rapport de deux termes consécutifs de la suite de Fibonacci converge vers le nombre d’or. Plus précisément, \(\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \varphi\). De plus, la formule de Binet exprime directement les termes de Fibonacci en fonction de puissances du nombre d’or.
Qu’est-ce qu’un rectangle d’or ?
Un rectangle d’or est un rectangle dont le rapport longueur/largeur est égal au nombre d’or φ. Sa propriété remarquable est que si on lui retire un carré, le rectangle restant est lui aussi un rectangle d’or. Cette propriété d’auto-similarité permet de construire la spirale d’or.
Où trouve-t-on le nombre d’or dans la nature ?
Le nombre d’or apparaît dans l’arrangement des feuilles sur les tiges (phyllotaxie), le nombre de pétales de certaines fleurs (souvent des nombres de Fibonacci : 3, 5, 8, 13, 21), les spirales de coquillages comme le nautile, et l’organisation des graines dans les tournesols ou les pommes de pin.
Pourquoi le nombre d’or est-il considéré comme esthétique ?
Les proportions basées sur le nombre d’or sont souvent perçues comme harmonieuses et équilibrées. Cependant, les études scientifiques sur la préférence esthétique universelle pour φ restent controversées. Son utilisation en art et architecture relève parfois plus de la tradition et du symbolisme que d’une loi esthétique absolue.
Comment calculer le nombre d’or ?
Pour calculer le nombre d’or, utilisez la formule \(\varphi = \frac{1 + \sqrt{5}}{2}\). Calculez d’abord \(\sqrt{5} \approx 2{,}236\), ajoutez 1 pour obtenir 3,236, puis divisez par 2 pour obtenir 1,618. Vous pouvez aussi le construire géométriquement avec une règle et un compas.
Quelle est la différence entre le nombre d’or et π (pi) ?
Le nombre d’or φ ≈ 1,618 est un nombre algébrique (solution d’une équation polynomiale) lié aux proportions géométriques. Le nombre π ≈ 3,14159 est un nombre transcendant lié aux cercles et à la circonférence. Ce sont deux constantes mathématiques différentes, sans relation directe, bien qu’elles apparaissent toutes deux fréquemment en géométrie.