Imaginez que vous lanciez une pièce de monnaie dix fois de suite. Combien de fois obtiendrez-vous « pile » ? Cette question simple cache en réalité l’un des concepts les plus puissants des probabilités : la loi binomiale. Découverte par le mathématicien suisse Jacques Bernoulli en 1713, elle permet de modéliser toutes les situations où l’on répète une expérience aléatoire avec seulement deux issues possibles. Des jeux de hasard aux tests médicaux, en passant par le contrôle qualité industriel, la loi binomiale est partout autour de nous.
Qu’est-ce qu’une Épreuve de Bernoulli ?
Avant d’aborder la loi binomiale, nous devons comprendre son fondement : l’épreuve de Bernoulli. Ce concept tire son nom du mathématicien Jacques Bernoulli et constitue la brique élémentaire de nombreuses situations probabilistes.
Définition : Épreuve de Bernoulli
Une épreuve de Bernoulli est une expérience aléatoire qui ne possède que deux issues possibles, traditionnellement appelées succès et échec. La probabilité d’obtenir un succès est notée \( p \), avec \( 0 \leq p \leq 1 \), et celle d’obtenir un échec est \( 1 – p \).
Prenons quelques exemples concrets pour mieux saisir cette notion :
- Lancer de pièce : Obtenir « pile » peut être considéré comme un succès, et « face » comme un échec.
- Lancer de dé : Si on s’intéresse à obtenir un « 6 », alors le succès est d’obtenir 6, et l’échec est d’obtenir 1, 2, 3, 4 ou 5. La probabilité de succès est alors \( p = \frac{1}{6} \).
- Test médical : Le résultat positif représente le succès, le résultat négatif représente l’échec.
- Contrôle qualité : Une pièce conforme correspond au succès, une pièce défectueuse à l’échec.
L’aspect crucial d’une épreuve de Bernoulli réside dans sa simplicité : il n’existe que deux possibilités mutuellement exclusives, et la probabilité reste constante à chaque réalisation.
Variable Aléatoire de Bernoulli
On peut associer à chaque épreuve de Bernoulli une variable aléatoire \( X \) qui prend :
- La valeur 1 en cas de succès, avec probabilité \( P(X = 1) = p \)
- La valeur 0 en cas d’échec, avec probabilité \( P(X = 0) = 1 – p \)
Cette variable suit ce qu’on appelle la loi de Bernoulli de paramètre \( p \), notée \( \mathcal{B}(p) \). Ses caractéristiques principales sont :
Le Schéma de Bernoulli : Répétition d’Épreuves Identiques
Dans la pratique, on effectue rarement une seule épreuve de Bernoulli. Pensez au joueur qui lance plusieurs fois une pièce, au médecin qui teste plusieurs patients, ou à l’usine qui contrôle plusieurs pièces. C’est ici qu’intervient le schéma de Bernoulli.
Définition : Schéma de Bernoulli
Un schéma de Bernoulli de paramètres \( n \) et \( p \) est une expérience aléatoire consistant à répéter \( n \) fois, de manière identique et indépendante, une même épreuve de Bernoulli de paramètre \( p \).
Les deux conditions essentielles sont :
- Identique : La probabilité de succès \( p \) reste constante à chaque épreuve.
- Indépendante : Le résultat d’une épreuve n’influence pas les suivantes.
⚠ Attention : Un tirage sans remise dans une urne ne constitue généralement pas un schéma de Bernoulli, car les probabilités changent après chaque tirage. En revanche, un tirage avec remise ou dans une population très grande peut être considéré comme un schéma de Bernoulli.
Représentation par Arbre de Probabilité
Un schéma de Bernoulli peut être visualisé grâce à un arbre de probabilité. Chaque niveau de l’arbre représente une épreuve, et chaque branche correspond soit au succès (probabilité \( p \)), soit à l’échec (probabilité \( 1 – p \)).
Par exemple, avec trois épreuves, le chemin « Succès-Échec-Succès » (noté S-E-S) a pour probabilité \( p \times (1-p) \times p = p^2(1-p) \).
Définition de la Loi Binomiale
Maintenant que nous maîtrisons les épreuves et schémas de Bernoulli, nous pouvons définir formellement la loi binomiale.
Définition : Loi Binomiale
Soit un schéma de Bernoulli composé de \( n \) épreuves identiques et indépendantes, chacune ayant une probabilité de succès \( p \). On note \( X \) la variable aléatoire comptant le nombre de succès obtenus parmi ces \( n \) épreuves.
On dit que \( X \) suit la loi binomiale de paramètres \( n \) et \( p \), ce que l’on note :
La variable aléatoire \( X \) prend ses valeurs dans l’ensemble \( \{0, 1, 2, \ldots, n\} \). Elle peut compter 0 succès (tous les résultats sont des échecs), 1 succès, 2 succès, et ainsi de suite jusqu’à \( n \) succès (tous les résultats sont des succès).
Exemple Fondamental
Une urne contient 5 boules gagnantes et 7 boules perdantes. On tire au hasard 4 boules successives avec remise. Soit \( X \) le nombre de boules gagnantes obtenues.
Analyse :
- Chaque tirage est une épreuve de Bernoulli (succès = tirer une boule gagnante).
- La probabilité de succès est \( p = \frac{5}{12} \) à chaque tirage.
- On répète l’expérience \( n = 4 \) fois de manière indépendante (avec remise).
- Donc \( X \sim \mathcal{B}\left(4, \frac{5}{12}\right) \).
Formule de Probabilité et Coefficients Binomiaux
Comment calculer la probabilité d’obtenir exactement \( k \) succès sur \( n \) épreuves ? C’est ici qu’interviennent les coefficients binomiaux.
Théorème : Loi de Probabilité Binomiale
Soit \( X \) une variable aléatoire qui suit la loi binomiale \( \mathcal{B}(n, p) \). Pour tout entier \( k \) tel que \( 0 \leq k \leq n \), la probabilité d’obtenir exactement \( k \) succès est donnée par :
où \( \binom{n}{k} \) (lu « \( k \) parmi \( n \) ») est le coefficient binomial défini par :
Interprétation de la Formule
Cette formule se décompose en trois parties essentielles :
- \( \binom{n}{k} \) : Le nombre de façons différentes d’obtenir exactement \( k \) succès parmi \( n \) épreuves. Par exemple, obtenir 2 succès sur 4 épreuves peut se faire selon les chemins S-S-E-E, S-E-S-E, S-E-E-S, E-S-S-E, E-S-E-S ou E-E-S-S, soit 6 chemins différents, ce qui correspond bien à \( \binom{4}{2} = 6 \).
- \( p^k \) : La probabilité d’obtenir \( k \) succès successifs.
- \( (1-p)^{n-k} \) : La probabilité d’obtenir \( n-k \) échecs.
Calcul des Coefficients Binomiaux
Les coefficients binomiaux peuvent être calculés de plusieurs manières :
Méthode 1 : Formule directe
Par exemple, pour calculer \( \binom{5}{2} \) :
Méthode 2 : Triangle de Pascal
Les coefficients binomiaux forment le célèbre triangle de Pascal. Chaque nombre est la somme des deux nombres situés au-dessus de lui :
| 1 |
| 1 1 |
| 1 2 1 |
| 1 3 3 1 |
| 1 4 6 4 1 |
| 1 5 10 10 5 1 |
La propriété fondamentale est :
Méthode 3 : Calculatrice
- Casio : Menu → OPTN → PROB → nCr
- TI : MATH → PRB → nCr
Espérance, Variance et Écart-Type de la Loi Binomiale
Les caractéristiques numériques d’une loi binomiale se calculent avec des formules remarquablement simples.
Théorème : Caractéristiques de la Loi Binomiale
Soit \( X \) une variable aléatoire suivant la loi binomiale \( \mathcal{B}(n, p) \). Alors :
Espérance :
Variance :
Écart-type :
Interprétation de l’Espérance
L’espérance \( E(X) = np \) représente le nombre moyen de succès que l’on peut espérer obtenir si l’on répète l’expérience un très grand nombre de fois. Par exemple, si vous lancez un dé 600 fois en cherchant à obtenir un « 6 », vous pouvez espérer obtenir en moyenne \( 600 \times \frac{1}{6} = 100 \) six.
Important : L’espérance n’est pas nécessairement une valeur que la variable aléatoire peut prendre. Si vous lancez 5 fois une pièce équilibrée, l’espérance de « pile » est 2,5, alors que vous ne pouvez obtenir que 0, 1, 2, 3, 4 ou 5 fois « pile ».
Interprétation de la Variance et de l’Écart-Type
La variance et l’écart-type mesurent la dispersion des valeurs autour de l’espérance. Plus ces valeurs sont grandes, plus les résultats peuvent s’éloigner de la moyenne attendue. Un écart-type faible indique que les résultats sont concentrés près de l’espérance.
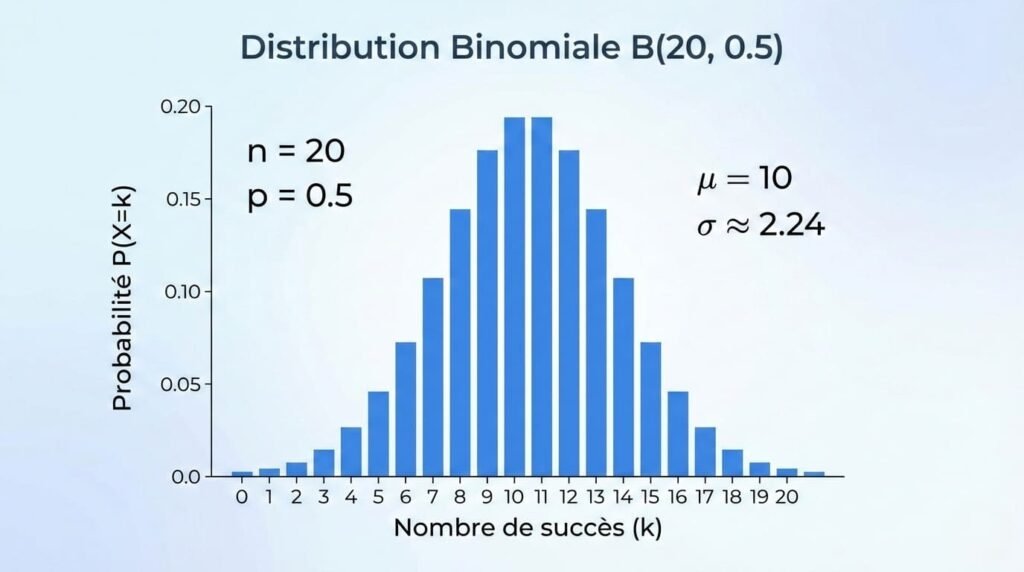
Représentation Graphique : Le Diagramme en Bâtons
La loi binomiale se représente graphiquement par un diagramme en bâtons, où chaque bâton de hauteur \( P(X = k) \) est placé à l’abscisse \( k \).
Observations importantes :
- La forme du diagramme dépend fortement de la valeur de \( p \) :
- Si \( p \) est proche de 0, le diagramme est concentré à gauche (peu de succès).
- Si \( p = 0,5 \), le diagramme est symétrique et centré sur \( \frac{n}{2} \).
- Si \( p \) est proche de 1, le diagramme est concentré à droite (beaucoup de succès).
- Le diagramme présente généralement une forme en cloche, surtout lorsque \( n \) est grand.
- Le diagramme est approximativement centré sur l’espérance \( E(X) = np \).
Conditions d’Application de la Loi Binomiale
Pour qu’une situation puisse être modélisée par une loi binomiale, toutes les conditions suivantes doivent être vérifiées :
Conditions Nécessaires
- On répète une même expérience aléatoire un nombre fixé \( n \) de fois.
- Chaque expérience ne possède que deux issues possibles : succès ou échec.
- Les expériences sont indépendantes les unes des autres.
- La probabilité de succès \( p \) reste constante à chaque épreuve.
- La variable aléatoire \( X \) compte le nombre de succès.
Erreur Fréquente : Ne confondez pas une loi binomiale avec le simple comptage d’événements dans une situation non répétée. Si vous ne répétez pas la même expérience, vous n’êtes pas dans le cadre d’une loi binomiale.
Applications Concrètes de la Loi Binomiale
La loi binomiale intervient dans de nombreux domaines pratiques :
Contrôle Qualité Industriel
Une usine produit des pièces dont 5% sont défectueuses. On prélève 20 pièces au hasard. Le nombre de pièces défectueuses suit \( \mathcal{B}(20, 0{,}05) \).
Médecine et Épidémiologie
Un test médical a une sensibilité de 95%. Si on teste 100 patients malades, le nombre de tests positifs suit approximativement \( \mathcal{B}(100, 0{,}95) \).
Sondages et Statistiques
Dans une population où 60% votent pour un candidat, si on interroge 50 personnes, le nombre de personnes favorables suit \( \mathcal{B}(50, 0{,}6) \).
Jeux de Hasard
Si on lance 10 fois un dé équilibré en cherchant à obtenir un « 6 », le nombre de six obtenus suit \( \mathcal{B}\left(10, \frac{1}{6}\right) \).
Calcul de Probabilités avec la Loi Binomiale
Voyons maintenant comment calculer concrètement des probabilités dans différentes situations.
Probabilité d’Obtenir Exactement k Succès
Exemple : On lance 5 fois une pièce équilibrée. Quelle est la probabilité d’obtenir exactement 3 fois « pile » ?
Solution :
Soit \( X \) le nombre de fois où on obtient « pile ». Alors \( X \sim \mathcal{B}(5, 0{,}5) \).
P(X = 3) &= \binom{5}{3} (0{,}5)^3 (1-0{,}5)^{5-3} \\
&= \frac{5!}{3! \times 2!} \times (0{,}5)^3 \times (0{,}5)^2 \\
&= 10 \times (0{,}5)^5 \\
&= 10 \times 0{,}03125 \\
&= 0{,}3125
\end{align*}
La probabilité est donc de 31,25%.
Probabilité d’Obtenir Au Moins k Succès
Pour calculer \( P(X \geq k) \), on utilise l’événement complémentaire :
Exemple : Une urne contient 9 jetons numérotés de 1 à 9. On tire avec remise 3 jetons. Quelle est la probabilité de tirer au moins un jeton pair ?
Solution :
Il y a 4 jetons pairs (2, 4, 6, 8) donc \( p = \frac{4}{9} \). Soit \( X \) le nombre de jetons pairs. Alors \( X \sim \mathcal{B}\left(3, \frac{4}{9}\right) \).
P(X \geq 1) &= 1 – P(X = 0) \\
&= 1 – \binom{3}{0} \left(\frac{4}{9}\right)^0 \left(\frac{5}{9}\right)^3 \\
&= 1 – \left(\frac{5}{9}\right)^3 \\
&= 1 – \frac{125}{729} \\
&= \frac{604}{729} \approx 0{,}828
\end{align*}
Probabilité d’Obtenir Au Plus k Succès
Pour calculer \( P(X \leq k) \), on additionne toutes les probabilités de 0 à \( k \) :
Utilisation de la Calculatrice pour la Loi Binomiale
Les calculatrices modernes possèdent des fonctions intégrées pour calculer rapidement les probabilités binomiales.
Sur Calculatrice Casio
Pour calculer \( P(X = k) \) :
- Appuyez sur MENU
- Sélectionnez STAT (statistiques)
- Choisissez DIST (distributions)
- Sélectionnez BINM (binomiale)
- Choisissez Bpd (Binomial Probability Distribution)
- Entrez : x (valeur de k), Numtrial (valeur de n), p (probabilité)
Pour calculer \( P(X \leq k) \) :
Suivez les mêmes étapes mais choisissez Bcd (Binomial Cumulative Distribution) au lieu de Bpd.
Sur Calculatrice TI
Pour calculer \( P(X = k) \) :
- Appuyez sur 2nd puis VARS (DISTR)
- Sélectionnez binompdf(
- Entrez : binompdf(n, p, k)
- Appuyez sur ENTER
Pour calculer \( P(X \leq k) \) :
- Appuyez sur 2nd puis VARS (DISTR)
- Sélectionnez binomcdf(
- Entrez : binomcdf(n, p, k)
- Appuyez sur ENTER
Astuce : Pour calculer \( P(X \geq k) \), utilisez : \( 1 – \text{binomcdf}(n, p, k-1) \)
Erreurs Fréquentes à Éviter
Erreur 1 : Confondre \( \binom{n}{k} \) avec \( n^k \). Le coefficient binomial compte les combinaisons, pas les arrangements avec répétition.
Erreur 2 : Oublier de vérifier l’indépendance des épreuves. Un tirage sans remise dans une petite population ne permet généralement pas d’utiliser une loi binomiale.
Erreur 3 : Confondre « au moins » et « au plus ». \( P(X \geq k) \neq P(X \leq k) \). Utilisez l’événement complémentaire quand c’est plus simple.
Erreur 4 : Penser que l’espérance doit être une valeur entière que la variable peut prendre. L’espérance peut être non entière même si \( X \) ne prend que des valeurs entières.
Erreur 5 : Confondre la formule de la variance : c’est \( np(1-p) \) et non \( np^2 \) ou \( n(1-p) \).
Lien avec d’Autres Lois de Probabilité
La loi binomiale entretient des relations intéressantes avec d’autres lois :
Lien avec la Loi de Bernoulli
Une loi binomiale \( \mathcal{B}(1, p) \) est exactement une loi de Bernoulli de paramètre \( p \). La loi binomiale généralise donc la loi de Bernoulli à \( n \) répétitions.
Approximation par la Loi Normale
Lorsque \( n \) est grand et que \( p \) n’est ni trop proche de 0 ni trop proche de 1, la loi binomiale peut être approximée par une loi normale de paramètres :
Cette approximation est valable lorsque \( np \geq 5 \) et \( n(1-p) \geq 5 \).
Lien avec la Loi de Poisson
Lorsque \( n \) est très grand et \( p \) très petit (tout en gardant \( np \) modéré), la loi binomiale peut être approximée par une loi de Poisson de paramètre \( \lambda = np \).
Conclusion et Points Clés à Retenir
La loi binomiale est un outil fondamental en probabilités qui modélise le nombre de succès dans une répétition d’épreuves indépendantes à deux issues. Voici les points essentiels à mémoriser :
- Une épreuve de Bernoulli possède exactement deux issues : succès (probabilité \( p \)) et échec (probabilité \( 1-p \)).
- Un schéma de Bernoulli répète \( n \) fois de manière identique et indépendante une épreuve de Bernoulli.
- La variable aléatoire \( X \) qui compte le nombre de succès suit la loi binomiale \( \mathcal{B}(n, p) \).
- La probabilité d’obtenir exactement \( k \) succès est donnée par : \( P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} \)
- L’espérance vaut \( E(X) = np \) et la variance \( V(X) = np(1-p) \).
- Les cinq conditions pour appliquer une loi binomiale sont : répétition, deux issues, indépendance, probabilité constante, et comptage des succès.
- Utilisez l’événement complémentaire pour simplifier les calculs de probabilités cumulées.
- La calculatrice est un outil précieux pour éviter les calculs fastidieux, surtout avec de grandes valeurs de \( n \).
La maîtrise de la loi binomiale ouvre la porte à de nombreuses applications pratiques dans les sciences, l’économie, la médecine et l’ingénierie. Elle constitue également une base solide pour comprendre d’autres lois de probabilité plus avancées.
Comment reconnaître qu’une variable suit une loi binomiale ?
Une variable aléatoire suit une loi binomiale si les cinq conditions suivantes sont réunies : on répète une même expérience aléatoire un nombre fixé de fois, chaque expérience a exactement deux issues possibles (succès ou échec), les expériences sont indépendantes, la probabilité de succès reste constante, et la variable compte le nombre total de succès obtenus.
Quelle est la différence entre un schéma de Bernoulli et une loi binomiale ?
Le schéma de Bernoulli désigne l’expérience aléatoire elle-même : la répétition de plusieurs épreuves de Bernoulli identiques et indépendantes. La loi binomiale, quant à elle, est la loi de probabilité de la variable aléatoire qui compte le nombre de succès obtenus dans ce schéma de Bernoulli. Le schéma est l’expérience, la loi est le modèle mathématique.
Comment calculer l’espérance d’une loi binomiale ?
L’espérance d’une loi binomiale de paramètres n et p se calcule très simplement avec la formule E(X) = np. Par exemple, si vous lancez 20 fois un dé en cherchant à obtenir un six, l’espérance est 20 × (1/6) ≈ 3,33 six en moyenne. Cette formule représente le nombre moyen de succès attendus.
Pourquoi utilise-t-on les coefficients binomiaux dans la formule ?
Les coefficients binomiaux comptent le nombre de façons différentes d’obtenir exactement k succès parmi n épreuves. Par exemple, obtenir 2 succès sur 4 épreuves peut se produire de 6 manières différentes (S-S-E-E, S-E-S-E, S-E-E-S, E-S-S-E, E-S-E-S, E-E-S-S), ce qui correspond au coefficient binomial C(4,2) = 6. Chaque chemin a la même probabilité p²(1-p)², donc on multiplie par le nombre de chemins.
Peut-on utiliser une loi binomiale pour un tirage sans remise ?
En général, non. Un tirage sans remise ne respecte pas la condition d’indépendance ni celle de probabilité constante, car les probabilités changent après chaque tirage. Cependant, si la population est très grande par rapport au nombre de tirages (règle pratique : population au moins 10 fois plus grande que l’échantillon), on peut considérer que les probabilités varient négligemment et utiliser une approximation binomiale.
Comment calculer la variance d’une variable binomiale ?
La variance d’une loi binomiale de paramètres n et p se calcule avec la formule V(X) = np(1-p). L’écart-type est alors la racine carrée de la variance : σ(X) = √[np(1-p)]. Par exemple, pour une loi B(10, 0,4), la variance vaut 10 × 0,4 × 0,6 = 2,4 et l’écart-type vaut environ 1,55. Ces valeurs mesurent la dispersion des résultats autour de l’espérance.