Limites et continuité : cours, théorèmes et exemples

Les limites et continuité constituent un pilier fondamental en analyse mathématique. Ce chapitre permet de comprendre le comportement des fonctions autour de points spécifiques et d'analyser leurs propriétés essentielles. Ces concepts trouvent des applications concrètes en physique, en économie et en ingénierie, notamment pour modéliser des phénomènes continus et prédire le comportement de systèmes dynamiques.

Limite d’une fonction en un point

La notion de limite d'une fonction décrit le comportement de cette fonction lorsque la variable s'approche d'une valeur donnée. Cette notion est essentielle pour analyser les variations et les discontinuités potentielles.

Résultats fondamentaux

Soit P et Q deux fonctions polynômes, et soit x0x_0 appartenant à l'ensemble des nombres réels et aa un nombre réel. Les résultats suivants s'appliquent :
Limite d'un polynôme
lim⁡x→x0P(x)=P(x0) \lim_{x \to x_0} P(x) = P(x_0)
Limite d'un quotient de fonctions
lim⁡x→x0P(x)Q(x)=P(x0)Q(x0) si Q(x0)≠0 \lim_{x \to x_0} \frac{P(x)}{Q(x)} = \frac{P(x_0)}{Q(x_0)} \text{ si } Q(x_0) \neq 0

Limites des fonctions trigonométriques

Les fonctions trigonométriques possèdent des propriétés de limite particulières :
lim⁡x→x0sin⁡(x)=sin⁡(x0)\lim_{x \to x_0} \sin(x) = \sin(x_0)
lim⁡x→x0cos⁡(x)=cos⁡(x0)\lim_{x \to x_0} \cos(x) = \cos(x_0)
lim⁡x→x0tan⁡(x)=tan⁡(x0) si x0≠π2+kπ,  k∈Z\lim_{x \to x_0} \tan(x) = \tan(x_0) \text{ si } x_0 \neq \frac{\pi}{2} + k\pi, \; k \in \mathbb{Z}

Limites remarquables importantes

Certaines limites sont particulièrement utiles pour résoudre des formes indéterminées :
Limite trigonométrique fondamentale
lim⁡x→0sin⁡(x)x=1 \lim_{x \to 0} \frac{\sin(x)}{x} = 1
lim⁡x→0tan⁡(x)x=1\lim_{x \to 0} \frac{\tan(x)}{x} = 1
lim⁡x→0sin⁡(ax)ax=1\lim_{x \to 0} \frac{\sin(ax)}{ax} = 1
lim⁡x→01−cos⁡(x)x2=12\lim_{x \to 0} \frac{1 - \cos(x)}{x^2} = \frac{1}{2}

Opérations sur les limites

Les propriétés des limites sont valables si xx tend vers a+a^+, a−a^-, +∞+\infty ou −∞-\infty. Les opérations fondamentales conservent les limites selon des règles précises de limite de somme, limite de produit, limite d'inverse et limite de quotient.

Limites à droite et à gauche

Il est essentiel de distinguer les limites à droite et les limites à gauche pour étudier le comportement local d'une fonction.

Exemple pratique

Considérons la fonction définie par :
f(x)=∣1−x2∣x2−1f(x) = \frac{|1 - x^2|}{x^2 - 1}
Pour étudier la limite de ff en x=1x = 1, nous devons calculer séparément les limites à droite et à gauche.Pour xx dans l'intervalle ouvert de moins un à un, si x<1x < 1, nous avons 1−x2>01 - x^2 > 0, donc :
f(x)=1−x2x2−1=−(x2−1)x2−1=−1f(x) = \frac{1 - x^2}{x^2 - 1} = \frac{-(x^2 - 1)}{x^2 - 1} = -1
Par conséquent :
lim⁡x→1−f(x)=−1\lim_{x \to 1^-} f(x) = -1
Pour x>1x > 1, nous avons 1−x2<01 - x^2 < 0, donc :
f(x)=−(1−x2)x2−1=x2−1x2−1=1f(x) = \frac{-(1 - x^2)}{x^2 - 1} = \frac{x^2 - 1}{x^2 - 1} = 1
Par conséquent :
lim⁡x→1+f(x)=1\lim_{x \to 1^+} f(x) = 1
Puisque les limites à gauche et à droite sont différentes, la fonction ff n'admet pas de limite en x=1x = 1.

Continuité d’une fonction numérique en un point

La continuité garantit qu'une fonction ne présente aucune rupture ou saut au point considéré. Cette propriété est cruciale pour l'analyse des fonctions et leurs applications.

Définition de la continuité

Soit ff une fonction définie sur un intervalle centré en aa. On dit que la fonction ff est continue en aa si elle admet une limite finie en aa et que cette limite est égale à la valeur de la fonction en ce point :
Condition de continuité
lim⁡x→af(x)=f(a) \lim_{x \to a} f(x) = f(a)

Continuité à droite et à gauche

Une fonction ff définie sur un intervalle de la forme [a,a+r[[a, a+r[ où r>0r > 0 est continue à droite de aa si elle admet une limite finie à droite en aa et :
lim⁡x→a+f(x)=f(a)\lim_{x \to a^+} f(x) = f(a)
De manière similaire, une fonction ff définie sur un intervalle de la forme ]a−r,a]]a-r, a] où r>0r > 0 est continue à gauche de aa si :
lim⁡x→a−f(x)=f(a)\lim_{x \to a^-} f(x) = f(a)

Prolongement par continuité

Soit ff une fonction dont l'ensemble de définition est DfD_f, et soit aa un réel tel que a∉Dfa \notin D_f mais pour lequel la limite existe :
lim⁡x→af(x)=l (finie)\lim_{x \to a} f(x) = l \text{ (finie)}
La fonction définie par f~(x)=f(x)\tilde{f}(x) = f(x) si x≠ax \neq a et f~(a)=l\tilde{f}(a) = l est une fonction continue en aa et s'appelle un prolongement par continuité de la fonction ff en aa.

Opérations sur les fonctions continues

Continuité sur un intervalle

Soit ff une fonction dont le domaine de définition est DfD_f, et soit un intervalle ouvert ]a,b[]a, b[ inclus dans DfD_f.On dit que ff est continue sur l'ouvert ]a,b[]a, b[ si elle est continue en tout point de cet intervalle. On dit que ff est continue sur [a,b[[a, b[ si elle est continue sur ]a,b[]a, b[ et à droite de aa. Enfin, on dit que ff est continue sur [a,b][a, b] si elle est continue sur ]a,b[]a, b[, à droite de aa et à gauche de bb.

Propriétés des opérations

Si ff et gg sont deux fonctions continues en aa, alors les fonctions suivantes sont également continues en aa :
  • La somme f+gf + g
  • Le produit f×gf \times g
  • La valeur absolue ∣f∣|f|
Si ff et gg sont deux fonctions continues en aa et g(a)≠0g(a) \neq 0, alors les fonctions 1g\frac{1}{g} et fg\frac{f}{g} sont continues en aa.Si ff est une fonction continue en aa et f(a)≥0f(a) \geq 0, alors la fonction f\sqrt{f} est continue en aa.

Fonctions usuelles continues

Toute fonction polynôme est continue sur l'ensemble des nombres réels. Les fonctions sinus et cosinus sont continues sur l'ensemble des nombres réels.

Continuité de la composition

Soient ff une fonction définie sur un intervalle II et gg une fonction définie sur un intervalle JJ tels que f(I)⊂Jf(I) \subset J et x0x_0 un élément de II.Si ff est continue en x0x_0 et gg continue en f(x0)f(x_0), alors la composée g∘fg \circ f est continue en x0x_0. Si ff est continue sur II et gg continue sur f(I)f(I), alors g∘fg \circ f est continue sur II.

Limite de composition

Soit uu une fonction définie sur un intervalle pointé de centre x0x_0 telle que :
lim⁡x→x0u(x)=l\lim_{x \to x_0} u(x) = l
Si vv est continue en ll, alors :
lim⁡x→x0v(u(x))=v(l)\lim_{x \to x_0} v(u(x)) = v(l)

Image d’un intervalle par une fonction continue

Image d’un segment

L'image d'un segment [a,b][a, b] par une fonction continue est le segment [m,M][m, M] où mm représente le minimum de f(x)f(x) pour xx dans [a,b][a, b] et MM représente le maximum de f(x)f(x) pour xx dans [a,b][a, b].

Cas particuliers

Si ff est continue croissante sur [a,b][a, b], alors :
f([a,b])=[f(a),f(b)]f([a, b]) = [f(a), f(b)]
Si ff est continue décroissante sur [a,b][a, b], alors :
f([a,b])=[f(b),f(a)]f([a, b]) = [f(b), f(a)]

Image d’un intervalle quelconque

L'image d'un intervalle par une fonction continue est toujours un intervalle. Cependant, l'intervalle II et son image f(I)f(I) par une fonction continue n'ont pas nécessairement la même forme.

Cas d’une fonction strictement monotone

Pour une fonction ff continue et strictement croissante sur un intervalle II avec a=inf⁡Ia = \inf I et b=sup⁡Ib = \sup I, l'image de l'intervalle dépend des limites aux bornes.Pour une fonction ff continue et strictement décroissante sur un intervalle II, les images des intervalles sont inversées selon le sens de variation.

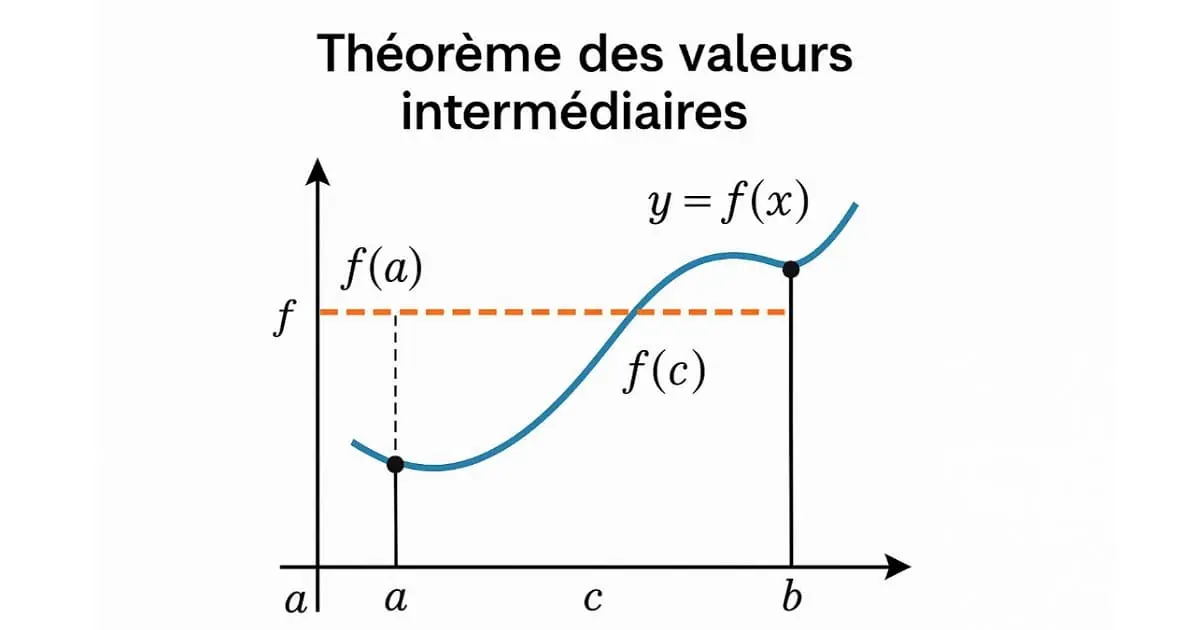
Théorème des valeurs intermédiaires

Cas général

Le théorème des valeurs intermédiaires affirme que soit ff une fonction continue sur [a,b][a, b]. Pour tout λ\lambda compris entre f(a)f(a) et f(b)f(b), il existe au moins un c∈[a,b]c \in [a, b] tel que :
Théorème des valeurs intermédiaires
f(c)=λ f(c) = \lambda TVI - limites et continuité

Cas fonction strictement monotone

Soit ff une fonction continue strictement monotone sur [a,b][a, b]. Pour tout λ\lambda compris entre f(a)f(a) et f(b)f(b), il existe un et un seul c∈[a,b]c \in [a, b] tel que f(c)=λf(c) = \lambda.Cette unicité signifie que l'équation f(x)=λf(x) = \lambda admet une solution unique dans [a,b][a, b].

Corollaires importants

Corollaire premier

Soit ff une fonction continue sur [a,b][a, b]. Si f(a)×f(b)<0f(a) \times f(b) < 0, alors il existe au moins un c∈[a,b]c \in [a, b] tel que f(c)=0f(c) = 0.

Corollaire second

Soit ff une fonction continue strictement monotone sur [a,b][a, b]. Si f(a)×f(b)<0f(a) \times f(b) < 0, alors il existe un et un seul cc dans [a,b][a, b] tel que f(c)=0f(c) = 0.

Fonctions composées et fonctions réciproques

Théorème d’existence

Soit ff une fonction définie, continue et strictement monotone sur un intervalle II. Alors ff admet une fonction réciproque notée f−1f^{-1} définie de J=f(I)J = f(I) vers II.

La fonction ff est une bijection de II vers f(I)f(I), et sa fonction réciproque vérifie :

f−1(y)=x  ⟺  y=f(x)f^{-1}(y) = x \iff y = f(x)
On a également les relations :
f−1(f(x))=x pour tout x∈If^{-1}(f(x)) = x \text{ pour tout } x \in I
f(f−1(y))=y pour tout y∈Jf(f^{-1}(y)) = y \text{ pour tout } y \in J

Propriétés de la fonction réciproque

Propriété de monotonie

Si ff admet une fonction réciproque f−1f^{-1} de J=f(I)J = f(I) vers II, alors f−1f^{-1} a la même monotonie sur JJ que celle de ff sur II.

Propriété géométrique

Si ff admet une fonction réciproque f−1f^{-1} de J=f(I)J = f(I) vers II, alors les courbes représentatives de f−1f^{-1} et de ff sont symétriques par rapport à la droite d'équation y=xy = x.Cette symétrie concerne toutes leurs composantes : les asymptotes, les tangentes et demi-tangentes.

La fonction racine n-ième

Définition et règles de calculs

Soit nn un élément de l'ensemble des entiers naturels non nuls. La fonction définie par f(x)=xnf(x) = x^n est une fonction continue strictement croissante sur l'ensemble des nombres réels positifs. Elle admet donc une fonction réciproque f−1f^{-1} de R+\mathbb{R}^+ vers R+\mathbb{R}^+.La fonction réciproque f−1f^{-1} s'appelle la fonction racine n-ième et se note xn\sqrt[n]{x}.

Conséquences de la définition

La fonction xn\sqrt[n]{x} est définie sur l'ensemble des nombres réels positifs. Pour tout x≥0x \geq 0, on a xn≥0\sqrt[n]{x} \geq 0. Pour tous réels positifs xx et yy, on a :
xn=y  ⟺  x=yn\sqrt[n]{x} = y \iff x = y^n
La fonction xn\sqrt[n]{x} est continue sur l'ensemble des nombres réels positifs et strictement croissante.

Propriétés importantes

xyn=xn⋅yn\sqrt[n]{xy} = \sqrt[n]{x} \cdot \sqrt[n]{y}
xnn=x pour tout x≥0\sqrt[n]{x^n} = x \text{ pour tout } x \geq 0
xpn=xpn pour tout x≥0 et p∈N\sqrt[n]{x^p} = x^{\frac{p}{n}} \text{ pour tout } x \geq 0 \text{ et } p \in \mathbb{N}
lim⁡x→+∞xn=+∞\lim_{x \to +\infty} \sqrt[n]{x} = +\infty

Règles de calcul

Pour tous réels positifs xx et yy, et pour tous entiers naturels non nuls nn et pp :
xyn=xn⋅yn\sqrt[n]{xy} = \sqrt[n]{x} \cdot \sqrt[n]{y}
xyn=xnyn pour y>0\sqrt[n]{\frac{x}{y}} = \frac{\sqrt[n]{x}}{\sqrt[n]{y}} \text{ pour } y > 0
xnp=xnp\sqrt[p]{\sqrt[n]{x}} = \sqrt[np]{x}
xpn=(xn)p\sqrt[n]{x^p} = (\sqrt[n]{x})^p

Résolution de l’équation

Pour résoudre l'équation xn=a\sqrt[n]{x} = a dans l'ensemble des nombres réels :

Exemples résolus

Équation première : x5=32\sqrt[5]{x} = 32Cette équation implique x≥0x \geq 0. En élevant à la puissance cinq, on obtient x=325=25=2x = 32^5 = 2^5 = 2. L'ensemble solution est donc S={2}S = \{2\}.Équation deuxième : x7=−128\sqrt[7]{x} = -128Cette équation implique x≥0x \geq 0. Puisque la racine septième est toujours positive ou nulle, mais le membre de droite est négatif, il y a contradiction. On obtient x=(−128)7=−2x = (-128)^7 = -2. L'ensemble solution est donc S={−2}S = \{-2\}.Équation troisième : x4=3\sqrt[4]{x} = 3Cette équation peut avoir deux solutions : x=34x = 3^4 ou x=(−3)4x = (-3)^4. L'ensemble solution est S={34,−34}S = \{\sqrt[4]{3}, -\sqrt[4]{3}\}.Équation quatrième : x6=−8\sqrt[6]{x} = -8La racine sixième d'un nombre est toujours positive ou nulle, et ne peut donc jamais égaler un nombre négatif. L'ensemble solution est vide : S=∅S = \emptyset.

Expression conjuguée

Les identités algébriques suivantes sont utiles pour simplifier les expressions contenant des racines cubiques :
a3−b3=(a−b)(a2+ab+b2)a^3 - b^3 = (a - b)(a^2 + ab + b^2)
a3+b3=(a+b)(a2−ab+b2)a^3 + b^3 = (a + b)(a^2 - ab + b^2)
Par conséquent, pour tous réels positifs xx et yy :
x3−y3=x−y(x3)2+x3y3+(y3)2\sqrt[3]{x} - \sqrt[3]{y} = \frac{x - y}{(\sqrt[3]{x})^2 + \sqrt[3]{x}\sqrt[3]{y} + (\sqrt[3]{y})^2}
x3+y3=x+y(x3)2−x3y3+(y3)2\sqrt[3]{x} + \sqrt[3]{y} = \frac{x + y}{(\sqrt[3]{x})^2 - \sqrt[3]{x}\sqrt[3]{y} + (\sqrt[3]{y})^2}

Puissance rationnelle

Puissance entière

Soit xx un réel et nn un entier naturel non nul. On définit :
xn=x×x×⋯×x⏟n foisx^n = \underbrace{x \times x \times \cdots \times x}_{n \text{ fois}}
Pour x≠0x \neq 0, on définit également :
x−n=1xnx^{-n} = \frac{1}{x^n}

Puissance rationnelle

Pour tout réel x≥0x \geq 0 et pour tout entier non nul qq, on pose :
x1q=xqx^{\frac{1}{q}} = \sqrt[q]{x}
Soit xx un réel positif et rr un rationnel, c'est-à-dire r=pqr = \frac{p}{q} où p∈Zp \in \mathbb{Z} et q∈N∗q \in \mathbb{N}^*. On définit la puissance rationnelle par :
Définition de la puissance rationnelle
xr=xpq=xpq=(xq)p x^r = x^{\frac{p}{q}} = \sqrt[q]{x^p} = (\sqrt[q]{x})^p

Propriétés des puissances rationnelles

Soit xx et yy deux réels positifs, et rr et r′r' des rationnels. Les propriétés suivantes s'appliquent :
xr×xr′=xr+r′x^r \times x^{r'} = x^{r + r'}
xrxr′=xr−r′\frac{x^r}{x^{r'}} = x^{r - r'}
(xr)r′=xr×r′(x^r)^{r'} = x^{r \times r'}
(xy)r=xr×yr(xy)^r = x^r \times y^r
(xy)r=xryr pour y>0\left(\frac{x}{y}\right)^r = \frac{x^r}{y^r} \text{ pour } y > 0

Résumé du cours Limites et continuité

Ce chapitre sur les limites et continuité constitue un pilier essentiel de l'analyse mathématique en deuxième année baccalauréat. Voici les points clés à retenir :
  • Limite d'une fonction : Permet d'étudier le comportement d'une fonction lorsque la variable s'approche d'une valeur donnée ou tend vers l'infini
  • Limites remarquables : Les rapports trigonométriques comme sinus x sur x tendent vers un lorsque x tend vers zéro
  • Continuité en un point : Une fonction est continue en un point si sa limite en ce point égale la valeur de la fonction
  • Opérations sur fonctions continues : La somme, le produit, le quotient et la composition de fonctions continues sont continues
  • Théorème des valeurs intermédiaires : Garantit l'existence de solutions pour les équations dans un intervalle
  • Fonction réciproque : Une fonction continue strictement monotone admet une fonction réciproque de même monotonie
  • Fonction racine n-ième : Réciproque de la fonction puissance n, définie sur les réels positifs
  • Puissances rationnelles : Extension des puissances entières aux exposants rationnels

Questions fréquentes sur les limites et continuité

Quelle est la différence entre limite et continuité ?

La limite décrit le comportement d'une fonction lorsqu'on s'approche d'un point, tandis que la continuité exige que la fonction soit définie au point et que sa limite égale sa valeur en ce point. Une fonction peut avoir une limite en un point sans y être continue si elle n'est pas définie en ce point ou si la limite diffère de la valeur de la fonction.

Comment calculer une limite de forme indéterminée ?

Pour résoudre une forme indéterminée comme zéro sur zéro ou l'infini sur l'infini, on peut utiliser plusieurs méthodes : la factorisation et simplification, les limites remarquables trigonométriques, la multiplication par l'expression conjuguée, ou le développement limité. Le choix de la méthode dépend de la nature de l'expression.

Quand utilise-t-on le théorème des valeurs intermédiaires ?

Le théorème des valeurs intermédiaires s'applique pour prouver l'existence de solutions d'une équation dans un intervalle donné. Il est particulièrement utile pour montrer qu'une équation admet au moins une solution lorsque la fonction change de signe sur l'intervalle. Si la fonction est strictement monotone, on garantit l'unicité de la solution.

Comment reconnaître si une fonction est continue ?

Pour vérifier la continuité, il faut s'assurer que la fonction est définie au point considéré, que la limite existe en ce point, et que cette limite égale la valeur de la fonction. Les fonctions polynômes, les fonctions trigonométriques sinus et cosinus, ainsi que les fonctions racines sont continues sur leurs domaines de définition respectifs.

Quelle est l’importance du prolongement par continuité ?

Le prolongement par continuité permet de combler un trou dans une fonction en lui attribuant la valeur de sa limite au point où elle n'était pas définie. Cette technique est essentielle en analyse pour étendre le domaine de définition d'une fonction tout en préservant ses propriétés de continuité, notamment pour les fonctions rationnelles présentant des simplifications.

Comment utiliser les limites remarquables en pratique ?

Les limites remarquables comme la limite de sinus x sur x égale un lorsque x tend vers zéro sont des outils puissants pour calculer des limites complexes. On les utilise en effectuant des substitutions appropriées ou en réécrivant l'expression pour faire apparaître la forme remarquable. Par exemple, pour calculer la limite de sinus trois x sur x, on multiplie et divise par trois pour obtenir trois fois sinus trois x sur trois x.

Pourquoi la fonction réciproque a-t-elle la même monotonie ?

Si une fonction est strictement croissante, des valeurs d'entrée plus grandes donnent des valeurs de sortie plus grandes. Pour la fonction réciproque, les rôles sont inversés mais la relation d'ordre est préservée. Ainsi, si la fonction originale est croissante de x vers y, alors la fonction réciproque qui va de y vers x est également croissante. Cette propriété découle directement de la définition de la bijection.

Comment simplifier les expressions avec des racines n-ièmes ?

Pour simplifier les expressions contenant des racines n-ièmes, on utilise les propriétés fondamentales : la racine d'un produit est le produit des racines, la racine d'un quotient est le quotient des racines, et on peut convertir les racines en puissances rationnelles pour faciliter les calculs. L'expression conjuguée est également utile pour rationaliser les dénominateurs contenant des racines cubiques.

Conclusion

La maîtrise des concepts de limites et continuité est fondamentale pour réussir en mathématiques au niveau du baccalauréat et constitue une base solide pour les études supérieures scientifiques. Ces notions permettent d'analyser rigoureusement le comportement des fonctions et de résoudre des problèmes complexes en analyse.Comme le dit le proverbe : « C'est en forgeant que l'on devient forgeron ». C'est en s'entraînant régulièrement aux calculs et exercices que l'on devient un mathématicien accompli. La pratique constante des techniques de calcul de limites, l'application du théorème des valeurs intermédiaires et la manipulation des fonctions continues sont essentielles pour développer une intuition mathématique solide.
Étiquettes
Partager