L’équation du second degré représente l’un des piliers fondamentaux de l’algèbre. Cette notion mathématique, étudiée depuis l’Antiquité babylonienne et systématisée par Al-Khwarizmi au IXe siècle, permet de résoudre une multitude de problèmes concrets en physique, en ingénierie et en économie. Comprendre comment résoudre ces équations vous ouvre les portes vers une maîtrise approfondie des fonctions polynomiales et de leurs applications pratiques.
Dans ce cours détaillé, nous allons explorer toutes les facettes des équations du second degré : de leur définition rigoureuse jusqu’aux méthodes de résolution les plus efficaces, en passant par le discriminant, la forme canonique et la factorisation. Vous découvrirez également comment ces équations modélisent des phénomènes réels comme la trajectoire d’un projectile ou l’optimisation d’une surface.
Qu’est-ce qu’une équation du second degré ?
Définition
Une équation du second degré (ou équation quadratique) est une équation polynomiale qui peut s’écrire sous la forme :
où \( a \), \( b \) et \( c \) sont des nombres réels appelés coefficients, avec la condition impérative que \( a \neq 0 \).
- \( a \) : coefficient du terme quadratique (ou coefficient de \( x^2 \))
- \( b \) : coefficient du terme linéaire (ou coefficient de \( x \))
- \( c \) : terme constant (ne dépend pas de \( x \))
- \( x \) : l’inconnue que nous cherchons à déterminer
Pourquoi a ne peut-il pas être nul ?
Si \( a = 0 \), l’équation se réduit à \( bx + c = 0 \), qui est une équation du premier degré. Le terme en \( x^2 \) est donc indispensable pour caractériser une équation du second degré.
Exemples d’équations du second degré
- \( x^2 – 5x + 6 = 0 \) avec \( a = 1 \), \( b = -5 \), \( c = 6 \)
- \( 3x^2 + 2x – 1 = 0 \) avec \( a = 3 \), \( b = 2 \), \( c = -1 \)
- \( -2x^2 + 7 = 0 \) avec \( a = -2 \), \( b = 0 \), \( c = 7 \)
- \( 4x^2 – 12x = 0 \) avec \( a = 4 \), \( b = -12 \), \( c = 0 \)
Le discriminant : clé de la résolution
Définition du discriminant
Le discriminant, noté \( \Delta \) (lettre grecque delta), est un nombre calculé à partir des coefficients de l’équation. Il est défini par la formule :
Le discriminant permet de déterminer le nombre et la nature des solutions de l’équation sans avoir à les calculer explicitement.
Interprétation du signe du discriminant
Le signe du discriminant détermine combien de solutions réelles possède l’équation :
| Signe de \( \Delta \) | Nombre de solutions | Nature des solutions |
|---|---|---|
| \( \Delta > 0 \) | Deux solutions distinctes | Deux nombres réels différents |
| \( \Delta = 0 \) | Une solution double | Un seul nombre réel (racine double) |
| \( \Delta < 0 \) | Aucune solution réelle | Deux solutions complexes conjuguées |
Exemple de calcul du discriminant
Soit l’équation \( 2x^2 – 7x + 3 = 0 \). Calculons son discriminant :
\Delta &= b^2 – 4ac \\
&= (-7)^2 – 4 \times 2 \times 3 \\
&= 49 – 24 \\
&= 25
\end{align*} \]
Comme \( \Delta = 25 > 0 \), cette équation admet deux solutions réelles distinctes.
Formules de résolution d’une équation du second degré
Théorème fondamental
Pour résoudre l’équation \( ax^2 + bx + c = 0 \) avec \( a \neq 0 \), on calcule d’abord le discriminant \( \Delta = b^2 – 4ac \), puis on applique les formules suivantes selon le cas :
Cas 1 : \( \Delta > 0 \) (deux solutions distinctes)
Cas 2 : \( \Delta = 0 \) (une solution double)
Cas 3 : \( \Delta < 0 \) (aucune solution réelle)
L’équation n’admet pas de solution dans l’ensemble des nombres réels \( \mathbb{R} \).
Exercice résolu détaillé
Énoncé : Résoudre l’équation \( 3x^2 – 5x – 2 = 0 \)
Solution :
\text{Étape 1 : } &\text{Identifier les coefficients} \\
&a = 3, \quad b = -5, \quad c = -2 \\[10pt]
\text{Étape 2 : } &\text{Calculer le discriminant} \\
\Delta &= b^2 – 4ac \\
&= (-5)^2 – 4 \times 3 \times (-2) \\
&= 25 + 24 \\
&= 49 \\[10pt]
\text{Étape 3 : } &\text{Analyser le discriminant} \\
&\Delta = 49 > 0 \text{ donc deux solutions distinctes} \\[10pt]
\text{Étape 4 : } &\text{Appliquer les formules} \\
x_1 &= \frac{-(-5) – \sqrt{49}}{2 \times 3} = \frac{5 – 7}{6} = \frac{-2}{6} = -\frac{1}{3} \\[10pt]
x_2 &= \frac{-(-5) + \sqrt{49}}{2 \times 3} = \frac{5 + 7}{6} = \frac{12}{6} = 2
\end{align*} \]
Ensemble solution : \( S = \left\{-\frac{1}{3} ; 2\right\} \)
Méthodes alternatives de résolution sans discriminant
Il existe des situations où calculer le discriminant n’est pas la méthode la plus rapide. Voici trois techniques alternatives :
Méthode 1 : Factorisation directe
Lorsque l’équation peut se factoriser facilement, on applique la règle du produit nul : un produit est nul si et seulement si l’un de ses facteurs est nul.
Exemple : Résoudre \( x^2 – 5x + 6 = 0 \)
x^2 – 5x + 6 &= 0 \\
(x – 2)(x – 3) &= 0
\end{align*} \]
Donc \( x – 2 = 0 \) ou \( x – 3 = 0 \), ce qui donne \( x = 2 \) ou \( x = 3 \)
Méthode 2 : Cas où c = 0 (factorisation par x)
Si le terme constant est nul, on peut factoriser par \( x \).
Exemple : Résoudre \( 2x^2 – 8x = 0 \)
2x^2 – 8x &= 0 \\
2x(x – 4) &= 0
\end{align*} \]
Donc \( 2x = 0 \) ou \( x – 4 = 0 \), ce qui donne \( x = 0 \) ou \( x = 4 \)
Méthode 3 : Cas où b = 0 (isoler x²)
Si le coefficient linéaire est nul, on peut isoler \( x^2 \).
Exemple : Résoudre \( 3x^2 – 27 = 0 \)
3x^2 – 27 &= 0 \\
3x^2 &= 27 \\
x^2 &= 9 \\
x &= \pm 3
\end{align*} \]
Donc \( x = -3 \) ou \( x = 3 \)
Méthode 4 : Reconnaissance d’une identité remarquable
Certaines équations correspondent à des formes remarquables.
Exemple : Résoudre \( x^2 – 6x + 9 = 0 \)
x^2 – 6x + 9 &= 0 \\
(x – 3)^2 &= 0 \\
x – 3 &= 0 \\
x &= 3
\end{align*} \]
Cette équation admet une solution double : \( x = 3 \)
Forme canonique d’un polynôme du second degré
Définition
La forme canonique d’un polynôme du second degré \( ax^2 + bx + c \) est de la forme :
où \( \Delta = b^2 – 4ac \) est le discriminant.
La forme canonique est particulièrement utile pour :
- Déterminer les coordonnées du sommet de la parabole représentant la fonction associée
- Trouver le minimum ou maximum de la fonction
- Résoudre l’équation de manière géométrique
Exemple de mise sous forme canonique
Mettons l’équation \( 2x^2 + 8x + 5 = 0 \) sous forme canonique :
2x^2 + 8x + 5 &= 2\left(x^2 + 4x\right) + 5 \\
&= 2\left(x^2 + 4x + 4 – 4\right) + 5 \\
&= 2\left[(x + 2)^2 – 4\right] + 5 \\
&= 2(x + 2)^2 – 8 + 5 \\
&= 2(x + 2)^2 – 3
\end{align*} \]
Le sommet de la parabole est au point de coordonnées \( (-2 ; -3) \).
Forme factorisée et relations entre coefficients et racines
Forme factorisée
Si l’équation \( ax^2 + bx + c = 0 \) admet deux racines \( x_1 \) et \( x_2 \) (c’est-à-dire si \( \Delta \geq 0 \)), alors le trinôme peut s’écrire sous forme factorisée :
Relations coefficients-racines (formules de Viète)
Lorsque l’équation admet deux racines \( x_1 \) et \( x_2 \), on a les relations suivantes :
\text{Somme des racines : } & x_1 + x_2 = -\frac{b}{a} \\[10pt]
\text{Produit des racines : } & x_1 \times x_2 = \frac{c}{a}
\end{align*} \]
Ces formules permettent de vérifier rapidement les solutions trouvées ou de reconstituer une équation à partir de ses racines.
Exemple d’application
Trouvons l’équation du second degré dont les racines sont \( x_1 = 3 \) et \( x_2 = -2 \) et dont le coefficient de \( x^2 \) est 1.
\text{Forme factorisée : } & (x – 3)(x – (-2)) = (x – 3)(x + 2) \\
\text{Développement : } & x^2 + 2x – 3x – 6 = x^2 – x – 6
\end{align*} \]
L’équation recherchée est donc \( x^2 – x – 6 = 0 \)
Vérifions avec les formules de Viète :
- Somme : \( 3 + (-2) = 1 = -\frac{-1}{1} \) ✓
- Produit : \( 3 \times (-2) = -6 = \frac{-6}{1} \) ✓
Signe d’un trinôme du second degré
Déterminer le signe d’un polynôme du second degré est essentiel pour résoudre des inéquations et analyser le comportement des fonctions.
Règle générale du signe
Soit \( f(x) = ax^2 + bx + c \) avec \( a \neq 0 \) et \( \Delta = b^2 – 4ac \) :
Si \( \Delta < 0 \) :
Le trinôme est toujours du signe de a pour tout \( x \in \mathbb{R} \)
Si \( \Delta = 0 \) :
Le trinôme est du signe de a pour tout \( x \neq x_0 \), et s’annule en \( x_0 = -\frac{b}{2a} \)
Si \( \Delta > 0 \) :
Soit \( x_1 < x_2 \) les deux racines. Le trinôme :
- est du signe de a à l’extérieur des racines : \( x < x_1 \) ou \( x > x_2 \)
- est du signe de -a entre les racines : \( x_1 < x < x_2 \)
- s’annule aux racines : \( x = x_1 \) ou \( x = x_2 \)
Tableau de signes
Pour une équation \( 2x^2 – 5x – 3 = 0 \) ayant pour racines \( x_1 = -\frac{1}{2} \) et \( x_2 = 3 \) :
| \( x \) | \( -\infty \) | \( -\frac{1}{2} \) | \( 3 \) | \( +\infty \) | |||
|---|---|---|---|---|---|---|---|
| \( 2x^2 – 5x – 3 \) | \( + \) | \( 0 \) | \( – \) | \( 0 \) | \( + \) |
Applications concrètes des équations du second degré
Physique : trajectoire d’un projectile
Lorsqu’on lance un objet en l’air, sa hauteur \( h(t) \) en fonction du temps suit une équation du second degré :
où \( g \) est l’accélération gravitationnelle, \( v_0 \) la vitesse initiale et \( h_0 \) la hauteur initiale.
Problème : Un ballon est lancé depuis le sol avec une vitesse de 20 m/s. Quand retombera-t-il au sol ? (On prend \( g = 10 \, \text{m/s}^2 \))
h(t) &= -5t^2 + 20t \\
\text{Au sol : } h(t) &= 0 \\
-5t^2 + 20t &= 0 \\
-5t(t – 4) &= 0
\end{align*} \]
Solutions : \( t = 0 \) (instant du lancer) ou \( t = 4 \) secondes (retour au sol)
Géométrie : problème d’optimisation
Problème : Un agriculteur dispose de 100 mètres de clôture pour entourer un champ rectangulaire. Quelles dimensions maximisent l’aire ?
Si \( x \) est la largeur, alors la longueur est \( 50 – x \). L’aire est :
La forme canonique révèle que l’aire maximale est atteinte pour \( x = 25 \) m, donnant une aire de 625 m².
Économie : analyse du profit
Une entreprise modélise son profit \( P(q) \) en fonction de la quantité produite \( q \) par :
Le profit maximal s’obtient au sommet de la parabole, soit pour \( q = 25 \) unités.
Résolution graphique d’une équation du second degré
Résoudre graphiquement \( ax^2 + bx + c = 0 \) revient à chercher les abscisses des points d’intersection de la parabole \( y = ax^2 + bx + c \) avec l’axe des abscisses (axe \( y = 0 \)).
Interprétation graphique selon le discriminant
- \( \Delta > 0 \) : La parabole coupe l’axe des abscisses en deux points distincts
- \( \Delta = 0 \) : La parabole est tangente à l’axe des abscisses (touche en un seul point)
- \( \Delta < 0 \) : La parabole ne coupe pas l’axe des abscisses
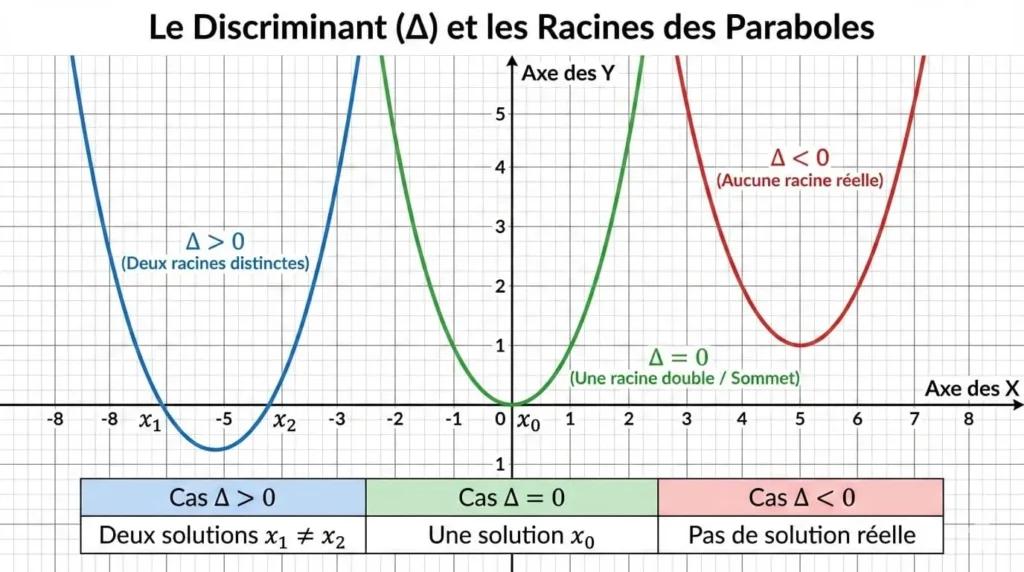
Propriétés de la parabole
- Si \( a > 0 \) : la parabole est tournée vers le haut (forme de U)
- Si \( a < 0 \) : la parabole est tournée vers le bas (forme de ∩)
- Le sommet a pour abscisse \( \alpha = -\frac{b}{2a} \)
- L’axe de symétrie de la parabole est la droite d’équation \( x = -\frac{b}{2a} \)
Erreurs fréquentes à éviter
- Oublier le signe moins dans la formule du discriminant : c’est \( -4ac \) et non \( +4ac \)
- Confondre les formules des racines : attention aux signes dans \( \frac{-b \pm \sqrt{\Delta}}{2a} \)
- Ne pas vérifier que a ≠ 0 : sans cette condition, l’équation n’est pas du second degré
- Oublier les deux solutions quand \( \Delta > 0 \) : il y a toujours deux valeurs distinctes
- Simplifier trop vite : vérifier que le discriminant est positif avant de calculer sa racine carrée
- Inverser \( 2a \) : le dénominateur est \( 2a \) dans toutes les formules, pas \( a \) seul
- Ne pas simplifier les racines carrées : \( \sqrt{50} = 5\sqrt{2} \) par exemple
Exercices d’entraînement
Exercice 1 : Identification et discriminant
Pour chacune des équations suivantes, identifier les coefficients \( a \), \( b \), \( c \), calculer le discriminant et en déduire le nombre de solutions :
- \( x^2 – 7x + 12 = 0 \)
- \( 2x^2 + 3x + 5 = 0 \)
- \( -x^2 + 4x – 4 = 0 \)
Exercice 2 : Résolution complète
Résoudre les équations suivantes en utilisant la méthode du discriminant :
- \( x^2 – 8x + 15 = 0 \)
- \( 3x^2 + 2x – 1 = 0 \)
- \( 4x^2 – 20x + 25 = 0 \)
Exercice 3 : Méthodes alternatives
Résoudre sans calculer le discriminant :
- \( x^2 – 9 = 0 \) (cas où \( b = 0 \))
- \( x^2 + 5x = 0 \) (cas où \( c = 0 \))
- \( x^2 + 10x + 25 = 0 \) (identité remarquable)
Exercice 4 : Problème appliqué
Un rectangle a un périmètre de 40 cm et une aire de 96 cm². Déterminer ses dimensions.
Indication : Poser \( x \) la longueur et \( y \) la largeur, puis établir un système d’équations qui mène à une équation du second degré.
Synthèse et points clés à retenir
- Une équation du second degré s’écrit \( ax^2 + bx + c = 0 \) avec \( a \neq 0 \)
- Le discriminant \( \Delta = b^2 – 4ac \) détermine le nombre de solutions
- Les formules des racines sont \( x = \frac{-b \pm \sqrt{\Delta}}{2a} \) quand \( \Delta \geq 0 \)
- La forme canonique permet de trouver le sommet de la parabole associée
- Les relations de Viète établissent des liens entre coefficients et racines
- Le signe du trinôme dépend du signe de \( a \) et de la position par rapport aux racines
- Les équations du second degré modélisent de nombreux phénomènes réels en sciences et en économie
Questions fréquemment posées
Comment résoudre une équation du second degré ?
Pour résoudre une équation du second degré \( ax^2 + bx + c = 0 \), commencez par calculer le discriminant \( \Delta = b^2 – 4ac \). Si \( \Delta > 0 \), utilisez les formules \( x = \frac{-b \pm \sqrt{\Delta}}{2a} \) pour obtenir deux solutions. Si \( \Delta = 0 \), il y a une solution double \( x = \frac{-b}{2a} \). Si \( \Delta < 0 \), il n’y a pas de solution réelle.
Qu’est-ce que le discriminant d’une équation du second degré ?
Le discriminant, noté \( \Delta \) (delta), est une valeur calculée par la formule \( \Delta = b^2 – 4ac \). Il permet de déterminer le nombre de solutions de l’équation sans les calculer : si \( \Delta > 0 \), il y a deux solutions ; si \( \Delta = 0 \), une solution double ; si \( \Delta < 0 \), aucune solution réelle.
Comment savoir si une équation est du second degré ?
Une équation est du second degré si elle peut s’écrire sous la forme \( ax^2 + bx + c = 0 \) où \( a \), \( b \), et \( c \) sont des constantes, avec la condition essentielle que \( a \neq 0 \). Le terme en \( x^2 \) doit être présent et avoir un coefficient non nul.
Quelle est la formule du discriminant ?
La formule du discriminant est \( \Delta = b^2 – 4ac \), où \( a \), \( b \), et \( c \) sont les coefficients de l’équation \( ax^2 + bx + c = 0 \). Cette formule est fondamentale pour déterminer la nature et le nombre des solutions de l’équation.
Peut-on résoudre une équation du second degré sans calculer le discriminant ?
Oui, il existe plusieurs méthodes alternatives : la factorisation directe quand c’est possible, la factorisation par \( x \) si \( c = 0 \), l’isolation de \( x^2 \) si \( b = 0 \), ou encore l’utilisation d’identités remarquables. Le choix de la méthode dépend de la forme particulière de l’équation.
Qu’est-ce que la forme canonique d’un trinôme du second degré ?
La forme canonique d’un trinôme \( ax^2 + bx + c \) s’écrit \( a(x – \alpha)^2 + \beta \) où \( \alpha = -\frac{b}{2a} \) et \( \beta \) est la valeur du trinôme en \( \alpha \). Cette forme met en évidence le sommet de la parabole au point \( (\alpha ; \beta) \) et facilite l’étude du signe et des variations.
Quelles sont les applications pratiques des équations du second degré ?
Les équations du second degré sont utilisées dans de nombreux domaines : en physique pour modéliser les trajectoires paraboliques et les mouvements uniformément accélérés, en géométrie pour les problèmes d’optimisation d’aires et de périmètres, en économie pour analyser les fonctions de coût et de profit, et en ingénierie pour calculer des structures et des résistances.
Que sont les formules de Viète ?
Les formules de Viète établissent des relations entre les racines et les coefficients d’une équation du second degré. Si \( x_1 \) et \( x_2 \) sont les racines de \( ax^2 + bx + c = 0 \), alors leur somme vaut \( x_1 + x_2 = -\frac{b}{a} \) et leur produit vaut \( x_1 \cdot x_2 = \frac{c}{a} \). Ces relations permettent de vérifier les solutions ou de reconstituer une équation.