Calculatrice Scientifique en Ligne : Gratuite et Rapide

Q: Comment choisir entre le mode DEG et RAD ?

Utilisez DEG (degrés) pour les exercices de lycée, les problèmes de géométrie classique, et lorsque les angles sont exprimés en degrés (exemple : 30°, 90°, 180°). Choisissez RAD (radians) pour le calcul infinitésimal, l'analyse mathématique, et lorsque vous travaillez avec des expressions comme π/6, π/2, etc. La formule de conversion est : 1 radian = 180/π degrés ≈ 57.2958°.

Q: Quelle est la différence entre log et ln ?

log (ou log₁₀) est le logarithme décimal (base 10). Il répond à la question : '10 élevé à quelle puissance donne ce nombre ?'. Exemple : log(1000) = 3 car 10³ = 1000. ln est le logarithme népérien ou logarithme naturel (base e ≈ 2.71828). Il est utilisé en calcul intégral, en physique (décroissance exponentielle), et en économie (intérêts composés continus). Exemple : ln(e) = 1 car e¹ = e.

Q: Pourquoi cos(90) ne donne-t-il pas exactement 0 sur certaines calculatrices ?

C'est dû aux erreurs de précision en virgule flottante. En informatique, les nombres décimaux sont représentés avec une précision limitée. Lorsque vous convertissez 90° en radians, puis calculez le cosinus, des erreurs d'arrondi microscopiques s'accumulent. Notre calculatrice corrige ce problème en arrondissant automatiquement les valeurs extrêmement proches de zéro à zéro exact, garantissant ainsi cos(90°) = 0.

Q: Comment calculer une factorielle (ex: 5!) ?

La factorielle d'un entier positif n (notée n!) est le produit de tous les entiers de 1 à n. Par exemple : 5! = 5 × 4 × 3 × 2 × 1 = 120. Sur cette calculatrice, saisissez simplement le nombre suivi du bouton x!. Les factorielles sont très utilisées en probabilités, combinatoire, et statistiques.

Q: Que signifie 'Infinity' comme résultat ?

Infinity (∞) apparaît dans trois cas principaux : 1) Division par zéro : 5/0 = Infinity. 2) Tangente de 90° : tan(90°) = Infinity. 3) Nombres extrêmement grands : valeurs dépassant 10¹⁵. Ce n'est pas une erreur, mais une représentation mathématique correcte selon les standards IEEE 754.

Q: Comment calculer une puissance (exemple : 2¹⁰) ?

Pour calculer une puissance x^y, appuyez sur le bouton x^y après avoir saisi la base. Exemple : pour calculer 2^10 : tapez 2, appuyez sur x^y (ou ^ au clavier), tapez 10, appuyez sur =. Résultat : 1024. Les puissances négatives sont aussi supportées : 2^(-3) = 0.125.

Calculatrice Scientifique : L’Outil Mathématique pour Vos Études

Pediamath-Calc

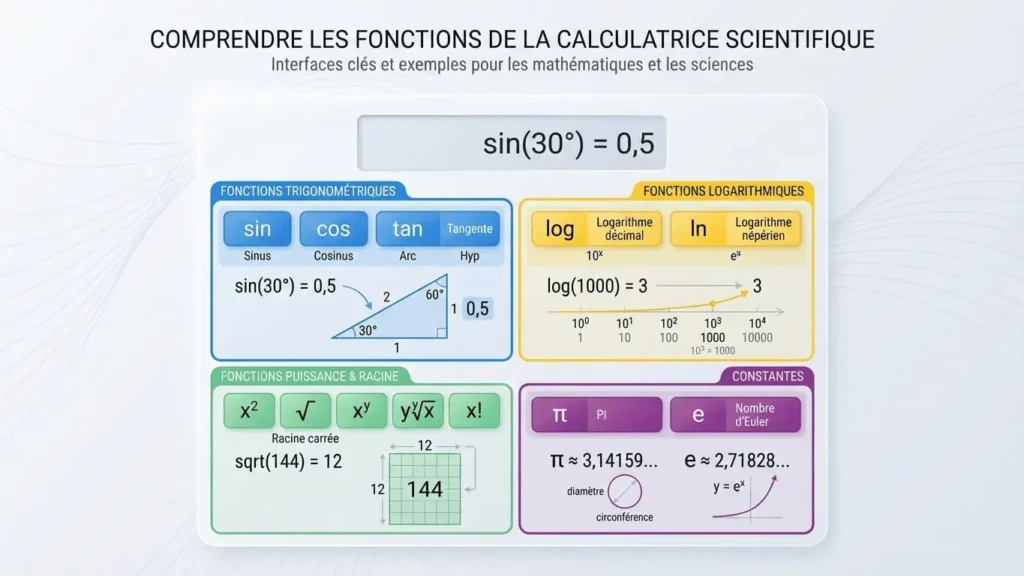
Une calculatrice scientifique est un instrument de calcul électronique conçu pour effectuer des opérations mathématiques avancées au-delà de l’arithmétique élémentaire. Contrairement à une calculatrice standard, elle intègre des fonctions trigonométriques (sinus, cosinus, tangente), des calculs logarithmiques (log, ln), des opérations exponentielles, et gère les constantes mathématiques fondamentales comme π (pi) et e (nombre d’Euler).

Notre calculatrice scientifique en ligne utilise la bibliothèque Math.js avec précision BigNumber (64 bits), garantissant des résultats exacts même pour les calculs décimaux complexes. Elle résout notamment le problème classique : 0.1 + 0.2 = 0.3 (et non 0.30000000000000004 comme avec JavaScript standard).

✨ Avantages Clés de Cet Outil

✓
Précision absolue : BigNumber 64 bits élimine les erreurs d’arrondi
✓
Mode DEG/RAD : Bascule entre degrés et radians pour la trigonométrie
✓
Historique des calculs : Affichage double ligne (expression + résultat)
✓
Fonction Ans : Réutilisation automatique du dernier résultat
✓
Gestion d’erreurs robuste : Messages clairs (Division par zéro → Infinity)

🎯 Pourquoi Choisir Cette Calculatrice Scientifique ?

Fonctionnalité	Notre Calculatrice	Calculatrices Standard
Précision des calculs décimaux	✓ BigNumber 64 bits	✗ Float 32 bits (erreurs)
Correction trigonométrique	✓ cos(90°)=0 exact	✗ 6.123e-17 (approx.)
Multiplication implicite	✓ 2π = 2×π	✗ Syntaxe manuelle
Validation des entrées	✓ Prévention ++ —	⚠ Variable
Gestion des erreurs	✓ Messages explicites	✗ « NaN » ou crash
Support clavier complet	✓ Raccourcis intégrés	⚠ Limité

📐 Guide de Syntaxe : Toutes les Fonctions Mathématiques

Cette calculatrice accepte une notation mathématique naturelle. Vous pouvez saisir vos expressions directement sans syntaxe compliquée.

Catégorie	Fonction	Syntaxe d’Entrée	Exemple de Calcul
Opérations de Base	Addition	`a + b`	`25 + 17 = 42`
	Soustraction	`a - b`	`100 - 37 = 63`
	Multiplication	`a × b` ou `a * b`	`8 × 7 = 56`
	Division	`a / b`	`144 / 12 = 12`
Trigonométrie	Sinus	`sin(angle)`	`sin(30) = 0.5` (en DEG)
	Cosinus	`cos(angle)`	`cos(60) = 0.5` (en DEG)
	Tangente	`tan(angle)`	`tan(45) = 1` (en DEG)
Logarithmes	Logarithme décimal (base 10)	`log(x)`	`log(1000) = 3`
Logarithmes	Logarithme népérien (base e)	`ln(x)`	`ln(e) = 1`
Puissances & Racines	Puissance	`x^y`	`2^10 = 1024`
	Racine carrée	`sqrt(x)` ou `√(x)`	`√(144) = 12`
	Factorielle	`n!`	`5! = 120`
Constantes	Pi (π)	`π`	`2π = 6.283185...`
Constantes	Nombre d’Euler (e)	`e`	`e^2 = 7.389056...`

💡 Astuce Pro : La calculatrice supporte la multiplication implicite. Vous pouvez écrire 2π au lieu de 2×π, ou 3sin(45) au lieu de 3×sin(45).

🎓 Mode d’Emploi : Utilisation Étape par Étape

Étape 1 : Choisir le Mode d’Angle (DEG ou RAD)

Avant d’effectuer des calculs trigonométriques, sélectionnez le mode approprié :

DEG (Degrés) : Pour les angles mesurés en degrés (0° à 360°). Recommandé pour les lycéens et la plupart des exercices scolaires.
RAD (Radians) : Pour les angles mesurés en radians (0 à 2π). Utilisé en mathématiques supérieures et en analyse.

Formule de conversion : \( 180° = \pi \text{ radians} \) donc \( \text{radians} = \text{degrés} \times \frac{\pi}{180} \)

Étape 2 : Saisir Votre Expression Mathématique

Utilisez les boutons de la calculatrice ou votre clavier pour entrer l’expression :

Exemple 1 : Calculer \( \sin(30°) + \cos(60°) \)

Appuyez sur sin
Tapez 30
Appuyez sur ) puis +
Appuyez sur cos
Tapez 60 puis )
Résultat : 1 (car 0.5 + 0.5 = 1)

Étape 3 : Utiliser les Parenthèses pour les Calculs Complexes

La calculatrice respecte l’ordre des opérations (priorité : parenthèses → puissances → multiplication/division → addition/soustraction).

❌ Sans parenthèses :

5 + 3 × 2 = 11

(multiplication d’abord)

✅ Avec parenthèses :

(5 + 3) × 2 = 16

(addition forcée en premier)

Étape 4 : Appuyer sur « = » pour Obtenir le Résultat

Le résultat s’affiche sur la ligne principale, tandis que votre expression complète reste visible dans l’historique (ligne supérieure).

Étape 5 : Réutiliser le Résultat avec « Ans »

Le bouton Ans (Answer) insère automatiquement le dernier résultat calculé. Très utile pour les calculs en chaîne !

📝 Exemple pratique :

Calculer 5 + 3 = 8
Puis multiplier par 2 : taper Ans × 2 = 16
Prendre la racine carrée : taper √(Ans) = 4

💡 Astuces Avancées et Avertissements

✨ Astuce #1 : Multiplication Implicite
Vous pouvez omettre le symbole de multiplication dans certains cas :
2π est interprété comme 2 × π
3sin(45) devient 3 × sin(45)
(2+3)(4+5) égale (2+3) × (4+5) = 45

⚡ Astuce #2 : Raccourcis Clavier
La calculatrice supporte la saisie clavier complète :
Enter ou = → Calculer le résultat
Esc ou C → Effacer tout (AC)
Backspace → Supprimer le dernier caractère (←)
0-9, +, -, *, /, (, ), . → Saisie directe

⚠️ Attention : Erreurs Courantes
Division par zéro : Le résultat affiche Infinity (conforme aux standards IEEE 754). Ce n’est pas une erreur, c’est le comportement mathématique correct.
Parenthèses non fermées : Une expression comme sin(30 (sans )) déclenche l’erreur « Parenthesis Error ».
Opérateurs consécutifs : 5++3 ou 2**4 sont bloqués par la validation d’entrée (sauf 5*-3 pour les nombres négatifs).
Mode DEG/RAD incorrect : Si vous calculez sin(π/6) en mode DEG au lieu de RAD, le résultat sera faux. Vérifiez toujours le mode !

🎯 Astuce #3 : Précision des Calculs
Cette calculatrice utilise BigNumber avec 64 bits de précision, ce qui signifie :
✅ 0.1 + 0.2 = 0.3 (exactement, sans erreur d’arrondi)
✅ cos(90°) = 0 (et non 6.123e-17 comme d’autres calculatrices)
✅ Les résultats sont arrondis intelligemment aux valeurs communes (0, 1, 0.5, etc.)

❓ Questions Fréquemment Posées (FAQ)

Comment choisir entre le mode DEG et RAD ?

Utilisez DEG (degrés) pour les exercices de lycée, les problèmes de géométrie classique, et lorsque les angles sont exprimés en degrés (exemple : 30°, 90°, 180°). Choisissez RAD (radians) pour le calcul infinitésimal, l’analyse mathématique, et lorsque vous travaillez avec des expressions comme \( \frac{\pi}{6} \), \( \frac{\pi}{2} \), etc. La formule de conversion est : \( 1 \text{ radian} = \frac{180}{\pi} \text{ degrés} \approx 57.2958° \).

Quelle est la différence entre log et ln ?

log (ou log₁₀) est le logarithme décimal (base 10). Il répond à la question : « 10 élevé à quelle puissance donne ce nombre ? ». Exemple : \( \log(1000) = 3 \) car \( 10^3 = 1000 \).

ln est le logarithme népérien ou logarithme naturel (base e ≈ 2.71828). Il est utilisé en calcul intégral, en physique (décroissance exponentielle), et en économie (intérêts composés continus). Exemple : \( \ln(e) = 1 \) car \( e^1 = e \).

Pourquoi cos(90) ne donne-t-il pas exactement 0 sur certaines calculatrices ?

C’est dû aux erreurs de précision en virgule flottante. En informatique, les nombres décimaux sont représentés avec une précision limitée (généralement 32 ou 64 bits en format IEEE 754). Lorsque vous convertissez 90° en radians (\( 90° = \frac{\pi}{2} \)), puis calculez le cosinus, des erreurs d’arrondi microscopiques s’accumulent, donnant un résultat comme 6.123233995736766e-17 au lieu de 0.

Notre calculatrice corrige ce problème en arrondissant automatiquement les valeurs extrêmement proches de zéro (< 10⁻¹⁰) à zéro exact, garantissant ainsi \( \cos(90°) = 0 \).

Comment calculer une factorielle (ex: 5!) ?

La factorielle d’un entier positif \( n \) (notée \( n! \)) est le produit de tous les entiers de 1 à \( n \). Par exemple : \( 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \).

Sur cette calculatrice, saisissez simplement le nombre suivi du bouton x!. Vous pouvez aussi taper directement 5! dans l’expression. Les factorielles sont très utilisées en probabilités, combinatoire, et statistiques.

Que signifie « Infinity » comme résultat ?

Infinity (∞) apparaît dans trois cas principaux :
1️⃣ Division par zéro : \( \frac{5}{0} = \text{Infinity} \) (mathématiquement, la limite tend vers l’infini).
2️⃣ Tangente de 90° : \( \tan(90°) = \text{Infinity} \) (car \( \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \) et \( \cos(90°) = 0 \)).
3️⃣ Nombres extrêmement grands : Valeurs dépassant 10¹⁵.

Ce n’est pas une erreur, mais une représentation mathématique correcte selon les standards IEEE 754.

Cette calculatrice est-elle autorisée en examen ?

En France, les calculatrices scientifiques sont autorisées aux examens depuis 1980, mais leur utilisation est strictement réglementée depuis 2000 (circulaire 99-186). Pour le Baccalauréat et la plupart des examens nationaux, seules les calculatrices sans connexion internet ni mémoire alphabétique sont permises.

Cette calculatrice en ligne nécessite une connexion internet, elle n’est donc pas autorisée en examen officiel. Cependant, elle est parfaite pour vos révisions, devoirs à la maison, et entraînement. Pour les examens, utilisez une calculatrice physique conforme (ex: Casio fx-92+, TI-Collège Plus, NumWorks).

Comment calculer une puissance (exemple : 2¹⁰) ?

Pour calculer une puissance \( x^y \), appuyez sur le bouton x^y après avoir saisi la base. Exemple : pour calculer \( 2^{10} \) :
1️⃣ Tapez 2
2️⃣ Appuyez sur x^y (ou tapez ^ au clavier)
3️⃣ Tapez 10
4️⃣ Appuyez sur =
Résultat : 1024 (car 2×2×2×2×2×2×2×2×2×2 = 1024).

Les puissances négatives sont aussi supportées : \( 2^{-3} = \frac{1}{2^3} = 0.125 \).

🔧 Résolution des Problèmes Courants

❌ Problème : « Syntax Error » ou « Format Error »

Cause : Expression mathématique mal formée (parenthèses non appariées, opérateurs mal placés).

Solution : Vérifiez que chaque parenthèse ouvrante ( a sa correspondante fermante ). Évitez les opérateurs consécutifs comme ++ ou **.

❌ Problème : Résultat trigonométrique inattendu

Cause : Mode d’angle incorrect (DEG au lieu de RAD, ou inversement).

Solution : Vérifiez le bouton actif en haut de la calculatrice. Si votre angle est en degrés, activez DEG. Si votre angle est une fraction de π (comme π/6), activez RAD.

❌ Problème : « Domain Error »

Cause : Opération mathématiquement impossible (racine carrée d’un nombre négatif en mode réel, logarithme de zéro ou d’un nombre négatif).

Solution : Vérifiez votre expression. Les logarithmes ne sont définis que pour les nombres strictement positifs : \( \log(x) \) nécessite \( x > 0 \). Pour les racines carrées de négatifs, vous sortez du domaine des nombres réels (nombres complexes).

Table des Matières