Le barycentre est un concept mathématique fondamental qui trouve ses racines dans la physique, notamment avec la notion de centre de gravité. En géométrie analytique, comprendre ce point particulier pour des systèmes de 2 ou 3 points pondérés permet de résoudre des problèmes complexes d’alignement, de division de segments et de construction géométrique. Ce cours détaillé vous présente toutes les formules essentielles, les propriétés fondamentales et des applications concrètes.
Rappels sur les Vecteurs
Définition et Propriétés des Vecteurs
Un vecteur \(\vec{u}\) est défini par trois caractéristiques : une direction, un sens et une longueur appelée norme.
La norme du vecteur \(\overrightarrow{AB}\) représente la longueur AB et se note \(\|\overrightarrow{AB}\|\). Ainsi : \(\|\overrightarrow{AB}\| = AB\).
Propriété fondamentale : Lorsque les points A, B, C et D ne sont pas alignés, on a l’équivalence suivante :
Relation de Chasles
La relation de Chasles est un outil essentiel pour manipuler les vecteurs :
Règle du parallélogramme : Pour trois points A, B et C, si D est tel que ABDC forme un parallélogramme, alors :
\[ \overrightarrow{AB} + \overrightarrow{AC} = \overrightarrow{AD} \]
Coordonnées dans un Repère
Dans un repère \((O ; \vec{i} ; \vec{j})\), dire que le point M a pour coordonnées \((x ; y)\) signifie que :
\[ \overrightarrow{OM} = x\vec{i} + y\vec{j} \]
On note alors \(M(x ; y)\) et de même pour un vecteur \(\vec{u}(x ; y)\).
Colinéarité de Vecteurs
Deux vecteurs non nuls \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont colinéaires s’ils ont la même direction, c’est-à-dire que les droites (AB) et (CD) sont parallèles.
Caractérisation algébrique : Ces vecteurs sont colinéaires s’il existe un réel \(k\) tel que :
\[ \overrightarrow{AB} = k\overrightarrow{CD} \]
Critère avec coordonnées : Les vecteurs \(\vec{u}(x ; y)\) et \(\vec{v}(x’ ; y’)\) sont colinéaires si et seulement si :
Théorème de Thalès Vectoriel
Soit ABC un triangle, M sur (AB) et N sur (AC). Si (MN) est parallèle à (BC), et si l’on note \(k\) le réel tel que \(\overrightarrow{AM} = k\overrightarrow{AB}\), alors :
\[ \overrightarrow{AN} = k\overrightarrow{AC} \quad \text{et} \quad \overrightarrow{MN} = k\overrightarrow{BC} \]
Réciproque : S’il existe un réel \(k\) tel que \(\overrightarrow{AM} = k\overrightarrow{AB}\) et \(\overrightarrow{AN} = k\overrightarrow{AC}\), alors les droites (MN) et (BC) sont parallèles.
Barycentre de Deux Points
Définition Générale
La notion mathématique présentée ici est intuitivement proche de la notion physique de centre de gravité. En fait, le centre de gravité est défini selon cette même logique.
Théorème (Définition) : Soient A et B deux points du plan, \(\alpha\) et \(\beta\) deux réels tels que \(\alpha + \beta \neq 0\). Il existe un unique point G tel que :
Ce point est appelé barycentre des deux points pondérés (A, \(\alpha\)) et (B, \(\beta\)). On note :
\[ G = \text{bar}\{(A, \alpha), (B, \beta)\} \]
Isobarycentre et Cas Particuliers
Si \(\alpha = \beta \neq 0\) (notamment si \(\alpha = \beta = 1\)), on dit que G est l’isobarycentre de A et B.
Remarque importante : L’isobarycentre de A et B est le milieu du segment [AB], c’est le point I tel que :
\[ \overrightarrow{IA} + \overrightarrow{IB} = \vec{0} \]
Propriété de Réduction
Théorème : Soient \(\alpha\) et \(\beta\) tels que \(\alpha + \beta \neq 0\), et soient A, B et G trois points du plan. On a l’équivalence :
Cette propriété est fondamentale car elle permet de calculer le point G à partir de n’importe quel point M du plan.
Position sur la Droite
Le point G associé à (A, \(\alpha\)) et (B, \(\beta\)) est toujours situé sur la droite (AB).
Règles de position :
- Si \(\alpha\) et \(\beta\) sont de même signe, alors \(G \in [AB]\)
- Si \(\alpha\) et \(\beta\) sont de signes contraires, alors \(G \notin [AB]\)
- Si \(|\alpha| > |\beta|\), alors G est plus près de A que de B
Analogie physique : Pensez à l’équilibre d’une barre avec une masse à chaque extrémité.
Propriété d’homogénéité : Pour tout nombre \(k\) non nul :
\[ \text{bar}\{(A, \alpha), (B, \beta)\} = \text{bar}\{(A, k\alpha), (B, k\beta)\} \]
Formule des Coordonnées pour Deux Points
Calcul pratique : Soit G le point recherché associé à (A, \(\alpha\)) et (B, \(\beta\)), et \((O ; \vec{i} ; \vec{j})\) un repère du plan.
Si \(A(x_A ; y_A)\) et \(B(x_B ; y_B)\), alors les coordonnées de G sont :
Exemple concret : Trouvons le point G associé à (A, 2) et (B, 3) avec \(A(1 ; 4)\) et \(B(7 ; -2)\).
Solution :
\[
\begin{align*}
x_G &= \frac{2 \times 1 + 3 \times 7}{2 + 3} = \frac{2 + 21}{5} = \frac{23}{5} = 4{,}6 \\
y_G &= \frac{2 \times 4 + 3 \times (-2)}{2 + 3} = \frac{8 – 6}{5} = \frac{2}{5} = 0{,}4
\end{align*}
\]
Donc \(G(4{,}6 \: ; \: 0{,}4)\).
Barycentre de Trois Points
Définition Générale
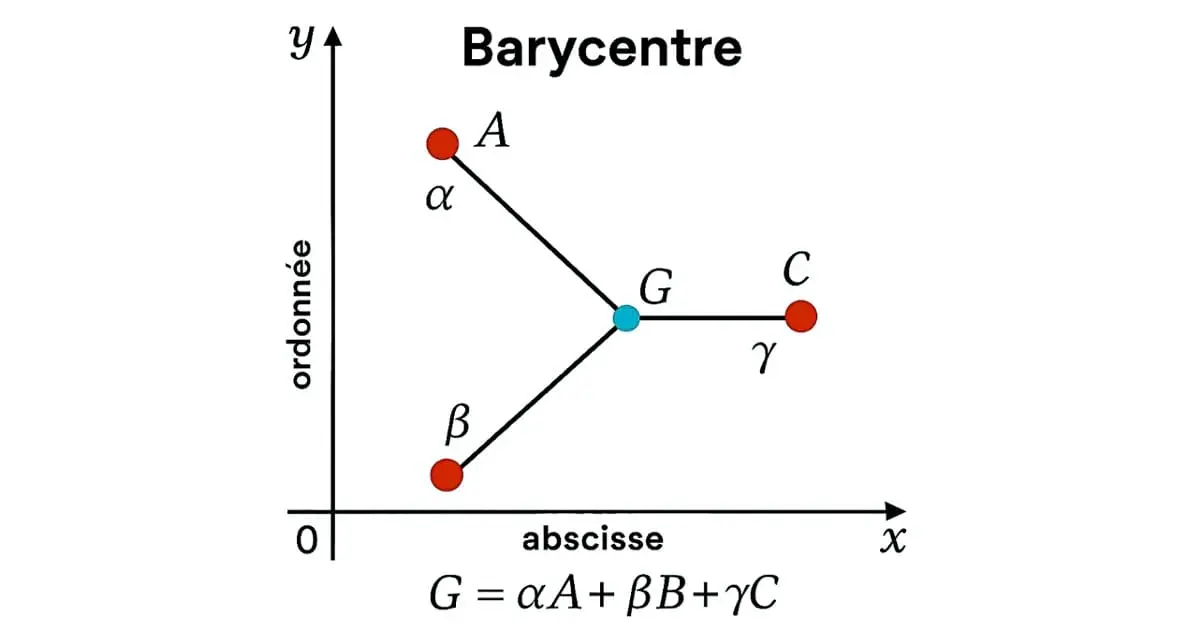
Théorème (Définition) : Soient A, B et C trois points du plan, \(\alpha\), \(\beta\) et \(\gamma\) trois réels tels que \(\alpha + \beta + \gamma \neq 0\). Il existe un unique point G tel que :
Ce point est appelé barycentre des trois points pondérés (A, \(\alpha\)), (B, \(\beta\)) et (C, \(\gamma\)). On note :
\[ G = \text{bar}\{(A, \alpha), (B, \beta), (C, \gamma)\} \]
Centre de Gravité d’un Triangle
Si \(\alpha = \beta = \gamma \neq 0\) (notamment si \(\alpha = \beta = \gamma = 1\)), on dit que G est l’isobarycentre de A, B et C.
Application importante : Par définition, le centre de gravité d’un triangle ABC correspond à l’isobarycentre des sommets A, B et C. On a donc :
\[ \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \vec{0} \]
Ce point correspond à l’intersection des médianes du triangle.
Propriété de Réduction (Trois Points)
Théorème : Soient \(\alpha\), \(\beta\) et \(\gamma\) tels que \(\alpha + \beta + \gamma \neq 0\), et soient A, B, C et G quatre points du plan. On a l’équivalence :
Théorème Partiel
L’analogie avec les centres de gravité de physique permet de mieux comprendre ce théorème. Il suffit de penser à l’équilibre d’une barre en T avec des poids aux trois extrémités.
Théorème partiel : Si \(H = \text{bar}\{(A, \alpha), (B, \beta)\}\), alors on a l’équivalence :
Cette propriété permet de décomposer le calcul d’un point complexe en plusieurs étapes plus simples.
Formule des Coordonnées pour Trois Points
Calcul général : Soit G le point associé à (A, \(\alpha\)), (B, \(\beta\)) et (C, \(\gamma\)), et \((O ; \vec{i} ; \vec{j})\) un repère du plan.
Si \(A(x_A ; y_A)\), \(B(x_B ; y_B)\) et \(C(x_C ; y_C)\), alors les coordonnées de G sont :
Exemple d’application : Calculons le centre de gravité G du triangle ABC avec \(A(2 ; 3)\), \(B(6 ; 1)\) et \(C(4 ; 7)\).
Solution : Le centre de gravité correspond à \(\alpha = \beta = \gamma = 1\).
\[
\begin{align*}
x_G &= \frac{2 + 6 + 4}{3} = \frac{12}{3} = 4 \\
y_G &= \frac{3 + 1 + 7}{3} = \frac{11}{3} \approx 3{,}67
\end{align*}
\]
Donc \(G\left(4 \: ; \: \frac{11}{3}\right)\).
Généralisation à n Points (Hors Programme)
Définition pour n Éléments
Théorème : Soient \(n\) points du plan \(A_1, A_2, \ldots, A_n\) et \(n\) réels \(\alpha_1, \alpha_2, \ldots, \alpha_n\) tels que \(\alpha_1 + \alpha_2 + \cdots + \alpha_n \neq 0\). Il existe un unique point G tel que :
\[ \alpha_1\overrightarrow{GA_1} + \alpha_2\overrightarrow{GA_2} + \cdots + \alpha_n\overrightarrow{GA_n} = \vec{0} \]
Ce point est appelé barycentre des n points pondérés \((A_1, \alpha_1), (A_2, \alpha_2), \ldots, (A_n, \alpha_n)\).
Formule des Coordonnées (n Points)
Dans un repère \((O ; \vec{i} ; \vec{j})\), si les points ont pour coordonnées \(A_1(x_{A_1} ; y_{A_1}), \ldots, A_n(x_{A_n} ; y_{A_n})\), alors :
Résumé du Cours
- Point pondéré de deux éléments : Le point G vérifiant \(\alpha\overrightarrow{GA} + \beta\overrightarrow{GB} = \vec{0}\) avec \(\alpha + \beta \neq 0\)
- Formule pratique (2 points) : \(G\left(\frac{\alpha x_A + \beta x_B}{\alpha + \beta} ; \frac{\alpha y_A + \beta y_B}{\alpha + \beta}\right)\)
- Système de trois éléments : Le point G vérifiant \(\alpha\overrightarrow{GA} + \beta\overrightarrow{GB} + \gamma\overrightarrow{GC} = \vec{0}\) avec \(\alpha + \beta + \gamma \neq 0\)
- Formule pratique (3 points) : \(G\left(\frac{\alpha x_A + \beta x_B + \gamma x_C}{\alpha + \beta + \gamma} ; \frac{\alpha y_A + \beta y_B + \gamma y_C}{\alpha + \beta + \gamma}\right)\)
- Propriété de réduction : \(\alpha\overrightarrow{MA} + \beta\overrightarrow{MB} = (\alpha + \beta)\overrightarrow{MG}\)
- Théorème partiel : Permet de décomposer le calcul en étapes
- Isobarycentre : Cas où tous les coefficients sont égaux (milieu, centre de gravité)
- Position : Toujours situé sur la droite passant par les points
Questions Fréquentes (FAQ)
Quelle est la formule pour calculer un point pondéré de deux éléments ?
Pour deux points A et B avec des coefficients \(\alpha\) et \(\beta\), le point G recherché a pour coordonnées : \(x_G = \frac{\alpha x_A + \beta x_B}{\alpha + \beta}\) et \(y_G = \frac{\alpha y_A + \beta y_B}{\alpha + \beta}\). Cette formule permet de calculer directement la position dans un repère.
Comment trouver le centre de gravité d’un triangle ?
Le centre de gravité (ou isobarycentre) du triangle ABC correspond au cas où les coefficients sont égaux (1, 1, 1). Ses coordonnées sont : \(x_G = \frac{x_A + x_B + x_C}{3}\) et \(y_G = \frac{y_A + y_B + y_C}{3}\). C’est le point d’intersection des trois médianes.
Quelle est la différence entre point pondéré général et isobarycentre ?
Un point pondéré général est défini avec des coefficients quelconques \(\alpha, \beta, \gamma\), tandis qu’un isobarycentre correspond au cas où tous les coefficients sont égaux. Par exemple, le milieu d’un segment [AB] est l’isobarycentre de A et B, et le centre de gravité d’un triangle est l’isobarycentre des trois sommets.
À quoi sert le théorème partiel ?
Le théorème partiel permet de simplifier le calcul d’un système de trois points (ou plus) en le décomposant en étapes. On calcule d’abord le point intermédiaire de deux éléments, puis on trouve le point final avec ce point intermédiaire et le troisième élément. Cela facilite grandement les calculs complexes.
Comment calculer un point pondéré pour un cercle ?
Pour calculer dans un cercle, on utilise les coordonnées cartésiennes des points situés sur le cercle. Si les points sont équidistants (polygone régulier), l’isobarycentre coïncide avec le centre du cercle. Dans le cas général, on applique les formules classiques avec les coordonnées des points concernés.
Quelle est la condition d’existence ?
La condition nécessaire et suffisante pour l’existence est que la somme des coefficients soit non nulle : \(\alpha + \beta + \gamma + \cdots \neq 0\). Si cette somme est nulle, le point recherché n’existe pas ou est rejeté à l’infini.