Le théorème fondamental de l’analyse est sans conteste l’un des résultats les plus importants du calcul différentiel et intégral. Ce théorème établit une relation profonde et remarquable entre deux opérations qui semblent a priori distinctes : la dérivation et l’intégration. Avant sa découverte au XVIIe siècle, personne ne soupçonnait que le calcul des aires sous les courbes et le calcul des tangentes étaient en réalité deux faces d’une même médaille mathématique.
Imaginons que vous roulez en voiture et que vous connaissez votre vitesse instantanée à chaque instant. Comment retrouver la distance totale parcourue ? Le théorème fondamental de l’analyse répond précisément à cette question : il suffit de calculer une primitive de la fonction vitesse. Cette intuition physique cache une vérité mathématique universelle qui transforme le calcul intégral en un outil puissant et élégant.
Définition et Contexte Historique
Qu’est-ce que le Théorème Fondamental de l’Analyse ?
En mathématiques, le théorème fondamental de l’analyse établit que les deux opérations de base de l’analyse, la dérivation et l’intégration, sont réciproques l’une de l’autre dans une certaine mesure. Ce théorème se présente sous deux formes complémentaires.
Historiquement, les mathématiciens grecs savaient déjà calculer des aires et des volumes à l’aide d’infinitésimaux. La notion de dérivation fut introduite au Moyen Âge. Mais c’est James Gregory qui publia en 1668 le premier énoncé partiel du théorème. Isaac Barrow en démontra une forme plus générale, et son élève Isaac Newton acheva de développer la théorie complète. Gottfried Wilhelm Leibniz systématisa ensuite ces résultats et introduisit les notations encore utilisées aujourd’hui.
Les Deux Théorèmes Fondamentaux
Le théorème fondamental de l’analyse comporte deux énoncés distincts mais étroitement liés. Chacun éclaire sous un angle différent la relation entre primitive et intégrale.
Premier Théorème Fondamental : L’intégrale comme primitive
Énoncé du Premier Théorème
Soit \( f \) une fonction continue sur un intervalle \( I \) et soit \( a \in I \). La fonction \( F \) définie sur \( I \) par :
F(x) = \int_{a}^{x} f(t) \, \mathrm{d}t
\]
est dérivable sur \( I \) et sa dérivée est égale à \( f \). Autrement dit :
F'(x) = f(x) \quad \text{pour tout } x \in I
\]
De plus, \( F \) est l’unique primitive de \( f \) qui s’annule en \( a \).
Second Théorème Fondamental : Calcul d’intégrale par primitive
Énoncé du Second Théorème
Soit \( f \) une fonction continue sur un intervalle fermé \([a, b]\) et soit \( F \) une primitive de \( f \) sur cet intervalle. Alors :
\int_{a}^{b} f(t) \, \mathrm{d}t = F(b) – F(a)
\]
On note également cette différence avec les crochets :
\int_{a}^{b} f(t) \, \mathrm{d}t = \left[ F(t) \right]_{a}^{b}
\]
Cette formule, appelée aussi formule de Leibniz-Newton, est d’une importance capitale car elle permet de calculer une intégrale définie simplement en connaissant une primitive de la fonction à intégrer, évitant ainsi le calcul laborieux des sommes de Riemann.
Hypothèses et Conditions d’Application
Pour que le théorème fondamental de l’analyse s’applique, certaines conditions doivent être respectées :
- Continuité de la fonction : La fonction \( f \) doit être continue sur l’intervalle considéré. Cette condition garantit l’existence de l’intégrale et de la primitive.
- Intervalle fermé : Pour le second théorème, on travaille généralement sur un intervalle fermé et borné \([a, b]\).
- Existence d’une primitive : Toute fonction continue sur un intervalle admet des primitives sur cet intervalle (c’est une conséquence du premier théorème).
Il existe des extensions du théorème pour des fonctions moins régulières (intégrable au sens de Lebesgue, fonctions réglées), mais dans le cadre du lycée et du début d’université, on se concentre sur les fonctions continues.
Explication Intuitive et Interprétation Physique
Reprenons l’exemple du déplacement en voiture mentionné en introduction. Supposons que vous voyagez en ligne droite à partir d’un point de départ à l’instant \( t = 0 \). À chaque instant \( t \), votre vitesse est donnée par une fonction \( v(t) \) et votre distance à l’origine est \( d(t) \).
La vitesse est le taux de variation instantané de la distance, autrement dit \( v(t) = d'(t) \). Si vous ne disposez que d’un compteur de vitesse qui affiche \( v(t) \), comment retrouver la distance parcourue \( d(t) \) ?
L’approche naturelle consiste à enregistrer la vitesse à intervalles réguliers (toutes les minutes par exemple), multiplier chaque vitesse par la durée de l’intervalle pour obtenir une distance élémentaire, puis additionner toutes ces distances. Cette somme est exactement une somme de Riemann. Lorsque les intervalles deviennent infiniment petits, la somme converge vers l’intégrale de la vitesse.
Le théorème fondamental de l’analyse dit précisément que pour retrouver \( d(t) \), il suffit de chercher une primitive de \( v(t) \). Mathématiquement :
d(t) – d(0) = \int_{0}^{t} v(s) \, \mathrm{d}s
\]
Cette relation illustre le second théorème : l’intégrale de la dérivée d’une fonction permet de retrouver la variation de cette fonction.
Interprétation Graphique
Graphiquement, le premier théorème fondamental peut s’interpréter ainsi : si \( F(x) \) représente l’aire sous la courbe de \( f \) entre \( a \) et \( x \), alors la dérivée de cette aire par rapport à \( x \) est égale à la hauteur de la courbe en \( x \), c’est-à-dire \( f(x) \).
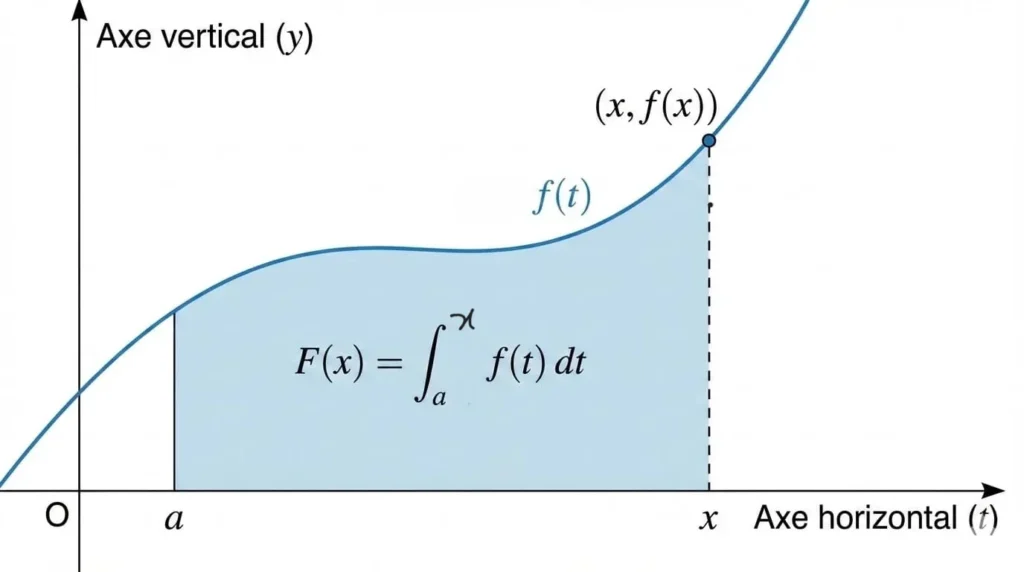
Le second théorème peut se visualiser de la manière suivante : pour calculer l’aire totale sous la courbe entre \( a \) et \( b \), on évalue une primitive \( F \) aux deux bornes et on prend leur différence \( F(b) – F(a) \).
Démonstration du Premier Théorème Fondamental
Nous allons démontrer que si \( f \) est continue sur \( I \) et si \( F(x) = \int_{a}^{x} f(t) \, \mathrm{d}t \), alors \( F'(x) = f(x) \).
Preuve
Fixons un point \( x_0 \in I \) et calculons le taux d’accroissement de \( F \) en \( x_0 \). Soit \( h \) un réel non nul tel que \( x_0 + h \in I \).
Étape 1 : Exprimons \( F(x_0 + h) – F(x_0) \)
F(x_0 + h) – F(x_0) = \int_{a}^{x_0+h} f(t) \, \mathrm{d}t – \int_{a}^{x_0} f(t) \, \mathrm{d}t
\]
Par la relation de Chasles (propriété d’additivité de l’intégrale), on a :
F(x_0 + h) – F(x_0) = \int_{x_0}^{x_0+h} f(t) \, \mathrm{d}t
\]
Étape 2 : Calculons le taux d’accroissement
\frac{F(x_0 + h) – F(x_0)}{h} = \frac{1}{h} \int_{x_0}^{x_0+h} f(t) \, \mathrm{d}t
\]
Étape 3 : Application du théorème de la moyenne
Puisque \( f \) est continue sur l’intervalle \([x_0, x_0+h]\) (ou \([x_0+h, x_0]\) si \( h < 0 \)), le théorème de la moyenne pour les intégrales garantit l'existence d'un point \( c_h \) entre \( x_0 \) et \( x_0 + h \) tel que :
\int_{x_0}^{x_0+h} f(t) \, \mathrm{d}t = h \cdot f(c_h)
\]
Donc :
\frac{F(x_0 + h) – F(x_0)}{h} = f(c_h)
\]
Étape 4 : Passage à la limite
Lorsque \( h \to 0 \), le point \( c_h \) tend vers \( x_0 \) (car il est compris entre \( x_0 \) et \( x_0 + h \)). Par continuité de \( f \) en \( x_0 \), on a :
\lim_{h \to 0} \frac{F(x_0 + h) – F(x_0)}{h} = \lim_{h \to 0} f(c_h) = f(x_0)
\]
Par définition de la dérivée, cela prouve que \( F'(x_0) = f(x_0) \). Puisque \( x_0 \) est arbitraire dans \( I \), le résultat est vrai pour tout \( x \in I \).
Démonstration du Second Théorème Fondamental
Preuve
Soit \( F \) une primitive de \( f \) sur \([a, b]\). D’après le premier théorème, la fonction \( G(x) = \int_{a}^{x} f(t) \, \mathrm{d}t \) est également une primitive de \( f \).
Puisque deux primitives d’une même fonction diffèrent d’une constante, il existe \( C \in \mathbb{R} \) tel que :
F(x) = G(x) + C \quad \text{pour tout } x \in [a, b]
\]
En évaluant en \( x = a \) :
F(a) = G(a) + C = \int_{a}^{a} f(t) \, \mathrm{d}t + C = 0 + C = C
\]
Donc \( C = F(a) \). Par conséquent :
F(x) = G(x) + F(a)
\]
En évaluant en \( x = b \) :
F(b) = G(b) + F(a) = \int_{a}^{b} f(t) \, \mathrm{d}t + F(a)
\]
D’où :
\int_{a}^{b} f(t) \, \mathrm{d}t = F(b) – F(a)
\]
Ce qui démontre le second théorème fondamental.
Applications et Prolongements
Le théorème fondamental de l’analyse trouve des applications dans de nombreux domaines :
- Physique : Calcul de distances à partir de vitesses, calcul de travail d’une force, énergie cinétique.
- Probabilités : Calcul de probabilités à partir de densités de probabilité.
- Économie : Calcul de surplus du consommateur et du producteur.
- Ingénierie : Calcul de volumes, de centres de gravité, de moments d’inertie.
Le théorème peut se généraliser au calcul vectoriel (théorème de Stokes) et aux fonctions de plusieurs variables. Il existe également des versions pour l’intégrale de Lebesgue et l’intégrale de Kurzweil-Henstock, permettant de traiter des fonctions moins régulières.
Résumé de cours
- Le théorème fondamental de l’analyse établit que dérivation et intégration sont des opérations inverses.
- Le premier théorème affirme que l’intégrale à borne variable d’une fonction continue est une primitive de cette fonction.
- Le second théorème permet de calculer une intégrale définie en évaluant une primitive aux bornes : intégrale de a à b de f égale F(b) moins F(a).
- Ce théorème s’applique aux fonctions continues sur un intervalle.
- Il transforme le calcul d’aires sous des courbes en un simple calcul de primitives.
- La démonstration repose sur le théorème de la moyenne et la continuité de la fonction.
- Applications majeures en physique, probabilités, économie et ingénierie.
- Maîtriser ce théorème, c’est comprendre l’une des plus belles connexions mathématiques : celle qui unit le local (la dérivée en un point) au global (l’intégrale sur un intervalle).