Le théorème des accroissements finis constitue l’un des résultats fondamentaux de l’analyse mathématique. Généralisation directe du théorème de Rolle, il établit un lien profond entre les variations d’une fonction et sa dérivée, permettant ainsi de relier des concepts locaux (la dérivée en un point) à des propriétés globales (l’accroissement entre deux points). Ce théorème trouve des applications essentielles dans l’étude de la monotonie des fonctions, le calcul d’encadrements, et constitue un outil indispensable pour démontrer de nombreuses inégalités en analyse.
Définition et Énoncé du Théorème
Théorème des Accroissements Finis (TAF)
Soient \( a \) et \( b \) deux nombres réels tels que \( a < b \). Soit \( f : [a, b] \to \mathbb{R} \) une fonction vérifiant les conditions suivantes :
- \( f \) est continue sur l’intervalle fermé \( [a, b] \)
- \( f \) est dérivable sur l’intervalle ouvert \( ]a, b[ \)
Alors il existe au moins un réel \( c \in ]a, b[ \) tel que :
f'(c) = \frac{f(b) – f(a)}{b – a}
\]
ou de manière équivalente :
f(b) – f(a) = f'(c)(b – a)
\]
Signification Mathématique
Le quotient \( \frac{f(b) – f(a)}{b – a} \) représente le taux d’accroissement moyen de la fonction \( f \) entre les points \( a \) et \( b \). Géométriquement, c’est le coefficient directeur de la droite sécante passant par les points \( A(a, f(a)) \) et \( B(b, f(b)) \). Le théorème affirme qu’il existe au moins un point \( c \) dans l’intervalle où la dérivée (c’est-à-dire la pente de la tangente) est égale à ce taux d’accroissement moyen.
Hypothèses et Conditions d’Application
Les hypothèses du théorème des accroissements finis doivent être scrupuleusement vérifiées avant toute application. Examinons-les en détail :
La Continuité sur l’Intervalle Fermé
La fonction doit être continue sur tout l’intervalle \( [a, b] \), y compris aux extrémités. Cette condition garantit que la fonction ne présente ni saut ni discontinuité. Sans continuité, le théorème peut être mis en défaut. Par exemple, la fonction définie par \( f(x) = 1 \) si \( x \neq 0 \) et \( f(0) = 0 \) n’est pas continue en zéro, et le théorème ne s’applique pas sur un intervalle contenant zéro.
La Dérivabilité sur l’Intervalle Ouvert
La dérivabilité est requise uniquement sur l’intervalle ouvert \( ]a, b[ \), excluant les extrémités. Cette distinction est importante car certaines fonctions peuvent être continues partout mais non dérivables en certains points. La fonction \( f(x) = |x| \) est continue sur \( [-1, 1] \) mais n’est pas dérivable en zéro. Toutefois, elle est dérivable sur \( ]-1, 0[ \) et sur \( ]0, 1[ \), permettant d’appliquer le théorème sur chacun de ces intervalles séparément.
Interprétation Géométrique
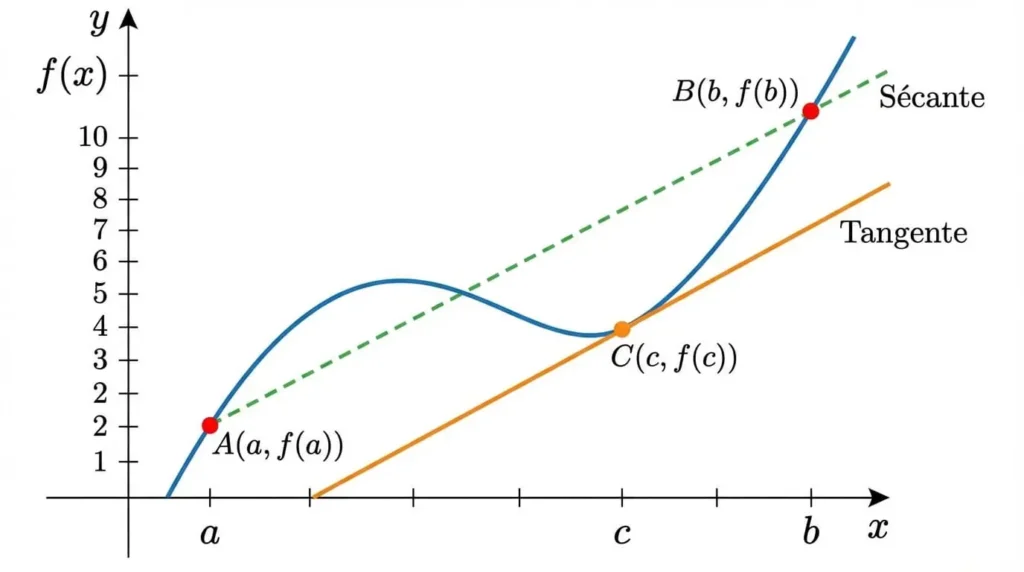
L’interprétation géométrique du théorème des accroissements finis est particulièrement éclairante. Considérons la courbe représentative de la fonction \( f \) et la droite sécante reliant les points \( A(a, f(a)) \) et \( B(b, f(b)) \). Cette sécante possède un coefficient directeur égal à \( \frac{f(b) – f(a)}{b – a} \).
Le théorème affirme qu’il existe au moins un point \( C(c, f(c)) \) sur la courbe, situé entre \( A \) et \( B \), où la tangente à la courbe est parallèle à cette sécante. Autrement dit, il existe un point où la pente instantanée (la dérivée) est égale à la pente moyenne.
Interprétation Cinématique
Si l’on considère \( f(t) \) comme la position d’un mobile à l’instant \( t \), alors \( f'(t) \) représente sa vitesse instantanée et \( \frac{f(b) – f(a)}{b – a} \) représente sa vitesse moyenne entre les instants \( a \) et \( b \). Le théorème des accroissements finis (TAF) affirme que si un véhicule parcourt une distance à la vitesse moyenne de 90 km/h, alors son compteur (indiquant la vitesse instantanée) a nécessairement affiché exactement 90 km/h au moins une fois durant le trajet. Cette formulation rend le théorème particulièrement intuitif.
Lien avec le Théorème de Rolle
Le théorème de Rolle constitue un cas particulier fondamental du théorème des accroissements finis. Rappelons son énoncé : si une fonction \( f \) est continue sur \( [a, b] \), dérivable sur \( ]a, b[ \) et vérifie \( f(a) = f(b) \), alors il existe au moins un point \( c \in ]a, b[ \) tel que \( f'(c) = 0 \).
On constate que si \( f(a) = f(b) \), alors le taux d’accroissement \( \frac{f(b) – f(a)}{b – a} = 0 \), et le théorème des accroissements finis nous donne \( f'(c) = 0 \), retrouvant exactement la conclusion du théorème de Rolle. Réciproquement, le théorème des accroissements finis se démontre en appliquant le théorème de Rolle à une fonction auxiliaire bien choisie, comme nous le verrons dans la démonstration.
Démonstration Rigoureuse
Démonstration du Théorème des Accroissements Finis (TAF)
Stratégie : L’idée consiste à construire une fonction auxiliaire \( g \) qui vérifie les hypothèses du théorème de Rolle, c’est-à-dire une fonction pour laquelle \( g(a) = g(b) \).
Construction de la fonction auxiliaire :
Définissons la fonction \( g : [a, b] \to \mathbb{R} \) par :
g(x) = f(x) – f(a) – (x – a) \times \frac{f(b) – f(a)}{b – a}
\]
Géométriquement, \( g(x) \) représente la différence entre la valeur de \( f(x) \) et la valeur correspondante sur la droite sécante passant par \( A \) et \( B \). C’est l’écart vertical entre la courbe et la sécante.
Vérification des hypothèses :
- Continuité : Puisque \( f \) est continue sur \( [a, b] \) et que les fonctions constantes et affines sont continues, leur combinaison linéaire \( g \) est également continue sur \( [a, b] \).
- Dérivabilité : La fonction \( f \) est dérivable sur \( ]a, b[ \), et la fonction affine \( x \mapsto f(a) + (x – a) \times \frac{f(b) – f(a)}{b – a} \) est dérivable sur \( \mathbb{R} \). Par conséquent, \( g \) est dérivable sur \( ]a, b[ \).
- Égalité aux extrémités : Calculons \( g(a) \) et \( g(b) \) :\[
g(a) = f(a) – f(a) – (a – a) \times \frac{f(b) – f(a)}{b – a} = 0
\]\[
g(b) = f(b) – f(a) – (b – a) \times \frac{f(b) – f(a)}{b – a} = f(b) – f(a) – (f(b) – f(a)) = 0
\]Donc \( g(a) = g(b) = 0 \).
Application du théorème de Rolle :
La fonction \( g \) vérifie toutes les hypothèses du théorème de Rolle sur \( [a, b] \). Il existe donc au moins un réel \( c \in ]a, b[ \) tel que \( g'(c) = 0 \).
Calcul de la dérivée et conclusion :
Calculons la dérivée de \( g \) :
g'(x) = f'(x) – \frac{f(b) – f(a)}{b – a}
\]
En appliquant la condition \( g'(c) = 0 \), nous obtenons :
f'(c) – \frac{f(b) – f(a)}{b – a} = 0
\]
d’où :
f'(c) = \frac{f(b) – f(a)}{b – a}
\]
Ce qui est exactement la conclusion du théorème des accroissements finis.
Forme Alternative avec le Paramètre θ
Le théorème des accroissements finis peut s’énoncer sous une forme équivalente particulièrement utile dans certaines applications. Pour toute fonction \( f \) dérivable sur un intervalle \( \mathcal{I} \) et pour tout point \( x_0 \in \mathcal{I} \), si \( x_0 + h \in \mathcal{I} \), alors il existe un nombre \( \theta_h \in ]0, 1[ \) tel que :
f(x_0 + h) – f(x_0) = h \cdot f'(x_0 + \theta_h h)
\]
Cette formulation met en évidence que l’accroissement \( f(x_0 + h) – f(x_0) \) est proportionnel à \( h \), avec un coefficient de proportionnalité égal à la dérivée évaluée en un point intermédiaire \( x_0 + \theta_h h \) situé strictement entre \( x_0 \) et \( x_0 + h \). Le paramètre \( \theta_h \) dépend généralement de \( h \) et n’est pas explicitement connu, mais son existence suffit pour de nombreuses applications théoriques.
Inégalité des Accroissements Finis
L’inégalité des accroissements finis généralise le théorème en remplaçant l’égalité par une inégalité lorsque la dérivée est bornée. Cette version est fondamentale car elle s’applique à des situations où la dérivée ne prend pas exactement une valeur donnée, mais reste dans un certain intervalle.
Inégalité des Accroissements Finis
Soit \( f : [a, b] \to \mathbb{R} \) une fonction continue sur \( [a, b] \) et dérivable sur \( ]a, b[ \). S’il existe un réel \( M \geq 0 \) tel que pour tout \( x \in ]a, b[ \), on ait \( |f'(x)| \leq M \), alors :
|f(b) – f(a)| \leq M(b – a)
\]
Démonstration : Par le théorème des accroissements finis, il existe \( c \in ]a, b[ \) tel que \( f(b) – f(a) = f'(c)(b – a) \). En prenant la valeur absolue et en utilisant l’hypothèse \( |f'(c)| \leq M \), nous obtenons directement \( |f(b) – f(a)| = |f'(c)||b – a| \leq M(b – a) \).
Une conséquence importante est le concept de fonction lipschitzienne. Une fonction vérifiant \( |f(x) – f(y)| \leq M|x – y| \) pour tous \( x, y \) dans son domaine est dite \( M \)-lipschitzienne. L’inégalité des accroissements finis montre que toute fonction dont la dérivée est bornée par \( M \) est \( M \)-lipschitzienne.
Applications Fondamentales
Monotonie et Signe de la Dérivée
L’application la plus célèbre du théorème des accroissements finis établit le lien entre le sens de variation d’une fonction et le signe de sa dérivée. Cette propriété, utilisée quotidiennement dans l’étude de fonctions, repose entièrement sur le théorème des accroissements finis.
Théorème : Monotonie et Dérivée
Soit \( I \) un intervalle et \( f : I \to \mathbb{R} \) une fonction dérivable sur \( I \). Alors :
- \( f \) est croissante sur \( I \) si et seulement si \( f'(x) \geq 0 \) pour tout \( x \in I \)
- \( f \) est décroissante sur \( I \) si et seulement si \( f'(x) \leq 0 \) pour tout \( x \in I \)
- \( f \) est constante sur \( I \) si et seulement si \( f'(x) = 0 \) pour tout \( x \in I \)
Démonstration du sens direct (croissance implique dérivée positive) : Si \( f \) est croissante, alors pour tout \( x \in I \) et tout \( h > 0 \) tel que \( x + h \in I \), le taux d’accroissement \( \frac{f(x + h) – f(x)}{h} \geq 0 \) car \( f(x + h) \geq f(x) \). En passant à la limite lorsque \( h \to 0^+ \), on obtient \( f'(x) \geq 0 \).
Démonstration de la réciproque (dérivée positive implique croissance) : Supposons \( f'(x) \geq 0 \) pour tout \( x \in I \). Soient \( a, b \in I \) avec \( a < b \). En appliquant le théorème des accroissements finis sur \( [a, b] \), il existe \( c \in ]a, b[ \) tel que \( f(b) - f(a) = f'(c)(b - a) \). Puisque \( f'(c) \geq 0 \) et \( b - a > 0 \), on a \( f(b) – f(a) \geq 0 \), donc \( f(b) \geq f(a) \). Ceci prouve que \( f \) est croissante.
Encadrement de Valeurs
L’inégalité des accroissements finis permet d’obtenir des encadrements précis de valeurs de fonctions. Par exemple, pour encadrer \( \cos(1) \), on sait que la dérivée de \( \cos(x) \) est \( -\sin(x) \), et \( |\sin(x)| \leq 1 \) pour tout \( x \). En appliquant l’inégalité des accroissements finis entre \( 0 \) et \( 1 \) :
|\cos(1) – \cos(0)| \leq 1 \times |1 – 0| = 1
\]
Puisque \( \cos(0) = 1 \), on obtient \( |\cos(1) – 1| \leq 1 \), soit \( 0 \leq \cos(1) \leq 2 \). Cet encadrement est certes large, mais il illustre le principe. Des encadrements plus fins peuvent être obtenus en utilisant des bornes plus précises de la dérivée sur des intervalles plus petits.
Limite de la Dérivée et Prolongement par Continuité
Le théorème des accroissements finis (TAF) permet également de démontrer un résultat important concernant le prolongement par continuité de la dérivée.
Théorème : Limite de la Dérivée
Soit \( f : [a, b] \to \mathbb{R} \) continue sur \( [a, b] \) et dérivable sur \( ]a, b] \). Si \( f’ \) admet une limite finie \( \ell \) en \( a \), alors \( f \) est dérivable à droite en \( a \) et \( f’_d(a) = \ell \).
Démonstration : Pour \( h > 0 \) suffisamment petit, appliquons le théorème des accroissements finis à \( f \) sur \( [a, a + h] \). Il existe \( c_h \in ]a, a + h[ \) tel que \( \frac{f(a + h) – f(a)}{h} = f'(c_h) \). Lorsque \( h \to 0^+ \), on a \( c_h \to a^+ \), donc \( f'(c_h) \to \ell \). Par conséquent, \( \lim_{h \to 0^+} \frac{f(a + h) – f(a)}{h} = \ell \), ce qui signifie que \( f \) est dérivable à droite en \( a \) avec \( f’_d(a) = \ell \).
Généralisation : Théorème de Cauchy
Le théorème des accroissements finis généralisé, également appelé théorème de la moyenne de Cauchy, étend le résultat au cas de deux fonctions.
Théorème de Cauchy
Soient \( f \) et \( g \) deux fonctions continues sur \( [a, b] \) et dérivables sur \( ]a, b[ \). Si \( g(a) \neq g(b) \), alors il existe \( c \in ]a, b[ \) tel que :
\frac{f(b) – f(a)}{g(b) – g(a)} = \frac{f'(c)}{g'(c)}
\]
à condition que \( g'(c) \neq 0 \).
Ce théorème se démontre de manière similaire au théorème des accroissements finis, en construisant une fonction auxiliaire appropriée. Il intervient notamment dans la démonstration de la règle de L’Hospital pour le calcul de limites de formes indéterminées.
Conclusion et Synthèse
Le théorème des accroissements finis (TAF) occupe une place centrale dans l’analyse mathématique en établissant un pont fondamental entre les propriétés locales (la dérivée) et les propriétés globales (les variations) d’une fonction. Sa démonstration élégante, reposant sur le théorème de Rolle et une fonction auxiliaire ingénieusement construite, illustre la puissance du raisonnement mathématique.
Les applications de ce théorème traversent toute l’analyse : étude de la monotonie, encadrements de valeurs, démonstration d’inégalités, unicité de solutions d’équations, et bien d’autres domaines. L’inégalité des accroissements finis, sa généralisation par Cauchy, et les liens avec les fonctions lipschitziennes montrent que ce résultat simple en apparence possède une richesse théorique considérable.
Pour maîtriser le théorème des accroissements finis, il est essentiel de bien comprendre ses hypothèses, de visualiser son interprétation géométrique, et de s’entraîner à l’appliquer dans des contextes variés. La prudence face aux pièges courants et une pratique régulière d’exercices permettent d’acquérir la rigueur nécessaire à son utilisation efficace, que ce soit au lycée pour l’étude de fonctions ou en université pour des démonstrations plus avancées en analyse réelle.