Imaginez que vous voyagez en avion de Paris à Rio de Janeiro. En quittant l’hémisphère nord pour rejoindre l’hémisphère sud, vous devez nécessairement traverser l’équateur à un moment précis du voyage. Cette idée intuitive illustre parfaitement le théorème des valeurs intermédiaires, un résultat fondamental de l’analyse mathématique qui garantit qu’une fonction continue « n’oublie » aucune valeur entre deux points.
Le théorème des valeurs intermédiaires, souvent abrégé en TVI, constitue l’un des piliers de l’étude des fonctions continues. Il permet de démontrer l’existence de solutions d’équations, de comprendre le comportement global des fonctions, et trouve des applications concrètes en physique, en ingénierie et en analyse numérique.
Définition et Énoncé du Théorème des Valeurs Intermédiaires
Définition précise
Théorème des Valeurs Intermédiaires (TVI)
Soit \( f \) une fonction définie et continue sur un intervalle \( [a;b] \), avec \( a < b \). Pour tout réel \( k \) compris entre \( f(a) \) et \( f(b) \), il existe au moins un réel \( c \in [a;b] \) tel que \( f(c) = k \).
Autrement dit, toutes les valeurs intermédiaires entre \( f(a) \) et \( f(b) \) sont effectivement atteintes par la fonction sur l’intervalle \( [a;b] \).
Forme alternative (Théorème de Bolzano)
Théorème de Bolzano (cas particulier avec \( k = 0 \))
Soit \( f \) une fonction continue sur \( [a;b] \). Si \( f(a) \) et \( f(b) \) sont de signes opposés, c’est-à-dire si \( f(a) \cdot f(b) \leq 0 \), alors il existe au moins un réel \( c \in [a;b] \) tel que \( f(c) = 0 \).
Cette formulation est particulièrement utile pour démontrer l’existence de racines (ou zéros) d’une fonction.
Hypothèses et Conditions d’Application
Pour que le théorème des valeurs intermédiaires s’applique, trois conditions doivent être réunies :
- La fonction doit être définie sur un intervalle fermé \( [a;b] \) : Les bornes \( a \) et \( b \) appartiennent au domaine de définition.
- La fonction doit être continue sur tout l’intervalle \( [a;b] \) : C’est la condition essentielle. Sans continuité, le théorème ne s’applique pas.
- La valeur \( k \) recherchée doit être comprise entre \( f(a) \) et \( f(b) \) : Cela signifie que \( k \in [\min(f(a), f(b)); \max(f(a), f(b))] \).
Pourquoi la continuité est-elle indispensable ?
La continuité garantit que la courbe de la fonction ne présente ni rupture, ni saut, ni discontinuité. Sans cette propriété, la fonction pourrait « sauter » au-dessus d’une valeur intermédiaire sans jamais l’atteindre.
Contre-exemple : Considérons la fonction partie entière \( E(x) \) sur \( [0;3] \). On a \( E(0) = 0 \) et \( E(3) = 3 \). Pourtant, la valeur \( k = 1{,}5 \) comprise entre 0 et 3 n’est jamais atteinte car la fonction partie entière ne prend que des valeurs entières. La fonction n’est pas continue, donc le TVI ne s’applique pas.
Énoncé Complet et Formulation Mathématique
Théorème des Valeurs Intermédiaires (énoncé rigoureux)
\begin{align*}
&\text{Soit } f : [a;b] \to \mathbb{R} \text{ une fonction continue.}\\
&\text{Soit } k \in \mathbb{R} \text{ tel que } \min(f(a), f(b)) \leq k \leq \max(f(a), f(b)).\\
&\text{Alors } \exists c \in [a;b], \quad f(c) = k.
\end{align*}
\]
Cette formulation met en évidence le caractère existentiel du théorème : il garantit l’existence d’au moins une solution, mais ne permet ni de calculer cette solution, ni d’affirmer son unicité (sauf sous conditions supplémentaires).
Interprétation Intuitive et Graphique
Analogie du voyage
Reprenons l’exemple du vol Paris-Rio. Votre altitude \( h(t) \) en fonction du temps \( t \) est une fonction continue (un avion ne peut pas « téléporter » d’une altitude à une autre). Si vous décollez à l’altitude \( h(0) = 100 \) m et atteignez une altitude de croisière \( h(T) = 11\,000 \) m, alors pour toute altitude intermédiaire \( k \) (par exemple 5 000 m), il existe nécessairement un instant \( c \) où vous étiez précisément à cette altitude.
Interprétation graphique
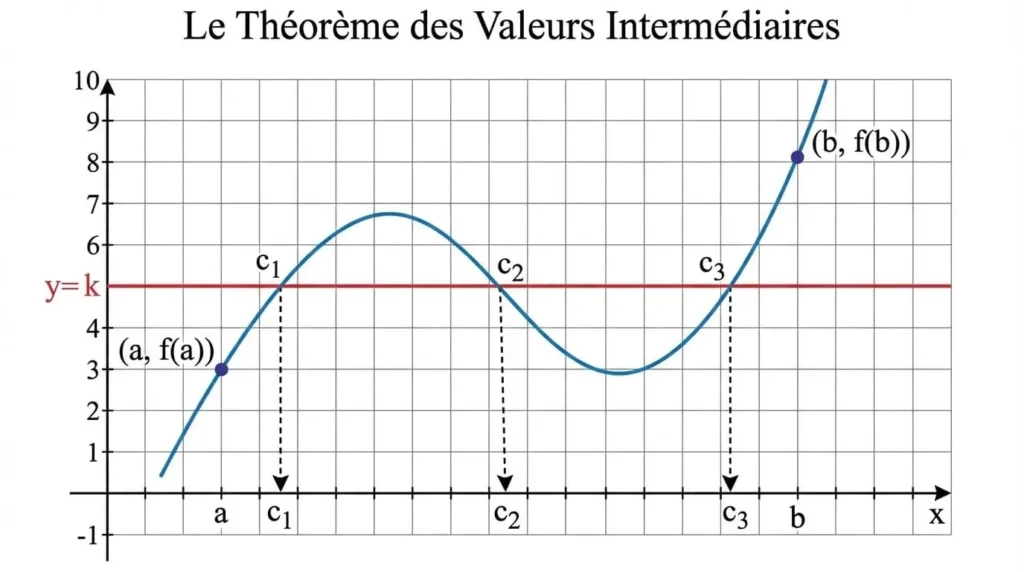
Sur le graphique, lorsqu’on trace une droite horizontale \( y = k \) (avec \( k \) compris entre \( f(a) \) et \( f(b) \)), cette droite coupe nécessairement la courbe de la fonction continue en au moins un point d’abscisse \( c \).
Ce que le TVI ne dit PAS
- Unicité de la solution : Le théorème garantit l’existence d’au moins une valeur \( c \), mais il peut y en avoir plusieurs (voire une infinité).
- Méthode de calcul : Le TVI est un théorème d’existence, pas de calcul. Il ne fournit pas de formule pour trouver \( c \).
Démonstration du Théorème des Valeurs Intermédiaires
Nous présentons ici la démonstration classique par la méthode de dichotomie, qui a l’avantage d’être constructive et de pouvoir être transformée en algorithme numérique.
Principe de la démonstration par dichotomie
L’idée consiste à couper successivement l’intervalle \( [a;b] \) en deux parties égales et à conserver celle où la solution doit se trouver. On construit ainsi deux suites adjacentes \( (a_n) \) et \( (b_n) \) qui convergent vers la valeur cherchée \( c \).
Démonstration rigoureuse
Sans perte de généralité, supposons \( f(a) \leq 0 \) et \( f(b) \geq 0 \) (cas où \( k = 0 \)). Si ce n’est pas le cas, on peut toujours se ramener à cette situation en considérant la fonction \( g(x) = f(x) – k \).
Construction des suites : On définit par récurrence deux suites \( (a_n) \) et \( (b_n) \) de la manière suivante :
\begin{align*}
&\text{Initialisation : } a_0 = a, \quad b_0 = b\\[0.5em]
&\text{Récurrence : Pour tout } n \in \mathbb{N}, \text{ on pose } m_n = \frac{a_n + b_n}{2}\\[0.5em]
&\quad\text{Si } f(m_n) \leq 0, \text{ alors }
\begin{cases}
a_{n+1} = m_n\\
b_{n+1} = b_n
\end{cases}\\[0.5em]
&\quad\text{Si } f(m_n) > 0, \text{ alors }
\begin{cases}
a_{n+1} = a_n\\
b_{n+1} = m_n
\end{cases}
\end{align*}
\]
Propriétés des suites construites : Par construction, on peut démontrer par récurrence que pour tout \( n \in \mathbb{N} \) :
- \( a_n \leq b_n \)
- \( f(a_n) \leq 0 \leq f(b_n) \)
- \( b_n – a_n = \frac{b-a}{2^n} \)
Convergence : La suite \( (a_n) \) est croissante et majorée par \( b \). La suite \( (b_n) \) est décroissante et minorée par \( a \). De plus, \( \lim_{n \to +\infty} (b_n – a_n) = \lim_{n \to +\infty} \frac{b-a}{2^n} = 0 \).
Les suites \( (a_n) \) et \( (b_n) \) sont donc adjacentes et convergent vers une même limite \( c \in [a;b] \).
Conclusion : Par continuité de \( f \) en \( c \), on a :
\lim_{n \to +\infty} f(a_n) = f(c) \quad \text{et} \quad \lim_{n \to +\infty} f(b_n) = f(c)
\]
Or, pour tout \( n \), \( f(a_n) \leq 0 \) et \( f(b_n) \geq 0 \). Par passage à la limite, on obtient \( f(c) \leq 0 \) et \( f(c) \geq 0 \), donc \( f(c) = 0 \).
Ceci achève la démonstration du théorème de Bolzano. Le cas général s’en déduit en considérant la fonction auxiliaire \( g(x) = f(x) – k \).
Corollaire du Théorème des Valeurs Intermédiaires
Image d’un intervalle par une fonction continue
Corollaire 1
L’image d’un intervalle par une fonction continue est un intervalle.
Plus précisément, si \( f \) est continue sur un intervalle \( I \), alors \( f(I) = \{f(x) \mid x \in I\} \) est également un intervalle (qui peut être ouvert, fermé, borné ou non).
Théorème de la bijection
Corollaire 2 (Théorème de la bijection)
Soit \( f \) une fonction continue et strictement monotone sur un intervalle \( [a;b] \). Alors pour tout réel \( k \) compris entre \( f(a) \) et \( f(b) \), l’équation \( f(x) = k \) admet une unique solution dans \( [a;b] \).
Ce corollaire ajoute la condition de monotonie stricte qui garantit l’unicité de la solution. Dans ce cas, \( f \) réalise une bijection de \( [a;b] \) sur \( f([a;b]) \), et possède donc une fonction réciproque.
Conditions du théorème de la bijection
Pour appliquer le théorème de la bijection, il faut vérifier trois hypothèses :
- \( f \) est définie sur \( [a;b] \)
- \( f \) est continue sur \( [a;b] \)
- \( f \) est strictement monotone (strictement croissante ou strictement décroissante) sur \( [a;b] \)
Méthode de Dichotomie et Application du TVI
Principe de la méthode de dichotomie
La démonstration du théorème des valeurs intermédiaires se traduit directement en un algorithme numérique appelé méthode de dichotomie. Cette méthode permet d’encadrer avec une précision arbitraire une solution de l’équation \( f(x) = 0 \).
Algorithme de dichotomie
Données : Une fonction continue \( f \), un intervalle \( [a;b] \) avec \( f(a) \cdot f(b) < 0 \), et une précision \( \varepsilon > 0 \).
Étapes :
- Calculer le milieu : \( m = \frac{a+b}{2} \)
- Calculer \( f(m) \)
- Si \( |b-a| < \varepsilon \), arrêter : la solution est encadrée dans \( [a;b] \)
- Si \( f(a) \cdot f(m) \leq 0 \), remplacer \( b \) par \( m \) (la solution est dans \( [a;m] \))
- Sinon, remplacer \( a \) par \( m \) (la solution est dans \( [m;b] \))
- Retourner à l’étape 1
Propriétés de la méthode
- Convergence garantie : L’algorithme converge toujours vers une solution
- Vitesse de convergence : À chaque itération, l’amplitude de l’intervalle est divisée par 2
- Nombre d’itérations : Pour obtenir une précision \( \varepsilon \), il faut environ \( n = \log_2\left(\frac{b-a}{\varepsilon}\right) \) itérations
Conclusion
Le théorème des valeurs intermédiaires constitue un résultat fondamental de l’analyse réelle. Il traduit mathématiquement l’intuition selon laquelle une fonction continue ne peut « sauter » aucune valeur intermédiaire. Ce théorème, bien que purement existentiel, trouve de nombreuses applications pratiques :
- Démonstration de l’existence de solutions d’équations
- Justification théorique des algorithmes de résolution numérique (dichotomie, Newton)
- Étude qualitative du comportement des fonctions
- Applications en physique et en ingénierie pour garantir l’existence de points d’équilibre
Retenez les trois conditions essentielles pour appliquer le TVI : une fonction définie sur un intervalle fermé, la continuité sur tout cet intervalle, et une valeur intermédiaire comprise entre les images des bornes. Le théorème de la bijection, corollaire enrichi du TVI, ajoute la garantie d’unicité lorsque la fonction est strictement monotone.
Maîtriser le théorème des valeurs intermédiaires et ses applications est indispensable pour progresser en analyse mathématique, que ce soit au lycée en classe de Terminale ou dans les premières années d’études supérieures scientifiques.