La fonction exponentielle représente l’une des fonctions mathématiques les plus fascinantes et utiles du programme de Terminale. Contrairement aux fonctions polynomiales classiques, elle possède une propriété remarquable : elle est égale à sa propre dérivée. Cette caractéristique unique fait d’elle un outil indispensable pour modéliser des phénomènes de croissance rapide, qu’il s’agisse de populations bactériennes, d’investissements financiers ou de désintégrations radioactives.
Dans ce cours complet, nous explorerons en profondeur cette fonction exceptionnelle, de sa définition rigoureuse jusqu’à ses applications concrètes. Vous découvrirez pourquoi les mathématiciens la considèrent comme l’une des fonctions les plus élégantes de l’analyse mathématique.
Définition de la fonction exponentielle
Définition fondamentale
La fonction exponentielle, notée \(\exp\) ou \(e^x\), est l’unique fonction dérivable sur \(\mathbb{R}\) qui vérifie simultanément les deux conditions suivantes :
- \(f'(x) = f(x)\) pour tout \(x \in \mathbb{R}\) (la dérivée est égale à la fonction elle-même)
- \(f(0) = 1\) (condition initiale)
Cette définition peut sembler abstraite, mais elle capture l’essence même de cette fonction. L’existence et l’unicité d’une telle fonction sont garanties par le théorème de Cauchy-Lipschitz, un résultat fondamental en analyse mathématique.
Le nombre e et la notation exponentielle
Le nombre \(e\) désigne la valeur prise par la fonction exponentielle en 1, c’est-à-dire \(e = \exp(1)\). Sa valeur approximative est :
Ce nombre irrationnel et transcendant joue un rôle central dans l’analyse. Grâce à lui, on peut écrire la fonction exponentielle sous forme de puissance : pour tout réel \(x\), on note \(\exp(x) = e^x\). Cette notation simplifie considérablement les calculs et rend les propriétés algébriques plus intuitives.
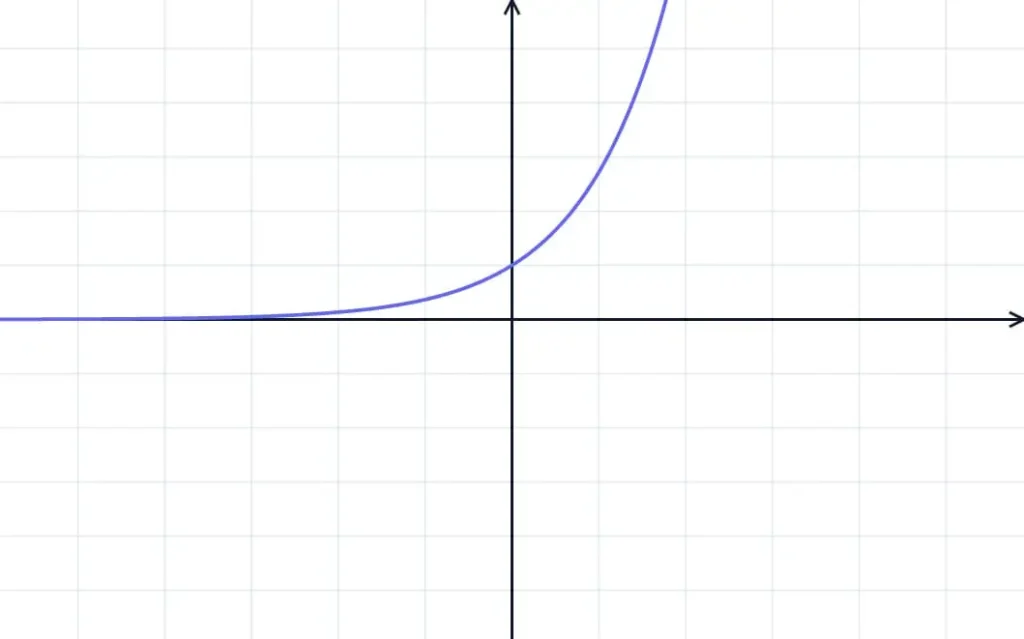
Développement en série
Une autre façon remarquable de définir la fonction exponentielle utilise son développement en série entière. Pour tout nombre réel \(x\), on peut écrire :
Cette formule converge pour toute valeur de \(x\) et permet notamment de calculer des valeurs approchées de la fonction exponentielle.
Propriétés algébriques de la fonction exponentielle
Les propriétés de la fonction exponentielle reproduisent exactement celles des puissances, ce qui justifie pleinement la notation \(e^x\).
Théorème : Propriétés opératoires
Pour tous nombres réels \(a\) et \(b\), et pour tout entier relatif \(n\), on a :
- Produit d’exponentielles : \(e^{a+b} = e^a \times e^b\)
- Quotient d’exponentielles : \(e^{a-b} = \dfrac{e^a}{e^b}\)
- Inverse : \(e^{-a} = \dfrac{1}{e^a}\)
- Puissance d’une exponentielle : \(\left(e^a\right)^n = e^{na}\)
- Racine : \(\sqrt{e^a} = e^{\frac{a}{2}}\)
Démonstration de la propriété fondamentale
Démontrons que \(e^{a+b} = e^a \times e^b\). Fixons \(b\) et considérons la fonction \(f\) définie par \(f(x) = \dfrac{e^{x+b}}{e^x}\). Calculons sa dérivée :
f'(x) &= \frac{e^{x+b} \times e^x – e^{x+b} \times e^x}{(e^x)^2} \\
&= \frac{e^{x+b} \times e^x – e^{x+b} \times e^x}{e^{2x}} \\
&= 0
\end{align*}
La fonction \(f\) ayant une dérivée nulle sur \(\mathbb{R}\), elle est constante. Or \(f(0) = \dfrac{e^b}{e^0} = \dfrac{e^b}{1} = e^b\). Donc pour tout \(x\), on a \(f(x) = e^b\), ce qui signifie \(\dfrac{e^{x+b}}{e^x} = e^b\), d’où \(e^{x+b} = e^x \times e^b\).
Exemples de simplifications
Appliquons ces propriétés pour simplifier des expressions :
Exemple 1 : Simplifier \(e^3 \times e^5 \times e^{-2}\)
Exemple 2 : Simplifier \(\dfrac{e^{7x}}{e^{2x}}\)
Exemple 3 : Simplifier \(\left(e^{2x+1}\right)^3\)
Étude complète de la fonction exponentielle
Ensemble de définition et signe
Théorème : Positivité stricte
Pour tout nombre réel \(x\), on a \(e^x > 0\). La fonction exponentielle est strictement positive sur \(\mathbb{R}\).
Démonstration : Pour tout réel \(x\), on peut écrire :
Or un carré est toujours positif ou nul. De plus, la fonction exponentielle ne s’annule jamais (sinon elle serait nulle partout par les propriétés algébriques), donc \(\left(e^{\frac{x}{2}}\right)^2 > 0\).
⚠ Erreur fréquente : Ne jamais écrire qu’une équation de type \(e^x = -3\) admet une solution. L’exponentielle étant toujours strictement positive, une telle équation n’a aucune solution dans \(\mathbb{R}\).
Dérivée de la fonction exponentielle
La propriété caractéristique de la fonction exponentielle est précisément qu’elle est égale à sa propre dérivée :
Théorème : Dérivée
La fonction exponentielle est dérivable sur \(\mathbb{R}\) et pour tout réel \(x\) :
Cette propriété remarquable se généralise aux fonctions composées. Si \(u\) est une fonction dérivable sur un intervalle \(I\), alors la fonction \(f\) définie par \(f(x) = e^{u(x)}\) est dérivable sur \(I\) et :
Exemple : Calculer la dérivée de \(f(x) = e^{3x^2-5x+1}\)
On pose \(u(x) = 3x^2 – 5x + 1\), donc \(u'(x) = 6x – 5\). Par conséquent :
Sens de variation
Théorème : Croissance stricte
La fonction exponentielle est strictement croissante sur \(\mathbb{R}\).
Démonstration : Pour tout réel \(x\), on a \(\left(e^x\right)’ = e^x > 0\). La dérivée étant strictement positive sur \(\mathbb{R}\), la fonction est strictement croissante.
Cette propriété a une conséquence importante pour la résolution d’équations et d’inéquations :
Conséquences de la croissance
Pour tous réels \(a\) et \(b\) :
- \(e^a = e^b \Leftrightarrow a = b\)
- \(e^a < e^b \Leftrightarrow a < b\)
- \(e^a \leq e^b \Leftrightarrow a \leq b\)
Limites aux bornes
Les limites de la fonction exponentielle en \(-\infty\) et \(+\infty\) sont essentielles pour comprendre son comportement asymptotique :
La première limite montre que l’axe des abscisses (droite d’équation \(y = 0\)) est une asymptote horizontale à la courbe représentative en \(-\infty\).
Croissances comparées
Un résultat fondamental concerne la comparaison entre la croissance exponentielle et les croissances polynomiales :
Théorème : Croissances comparées
Pour tout entier naturel \(n\), on a :
\[ \lim_{x \to -\infty} x^n e^x = 0 \]
Ce théorème exprime que l’exponentielle croît plus vite que n’importe quelle puissance de \(x\), et que l’exponentielle de \(-x\) décroît plus vite que l’inverse de n’importe quelle puissance.
Tableau de variations complet
| \(x\) | \(-\infty\) | \(0\) | \(+\infty\) | ||
|---|---|---|---|---|---|
| \((e^x)’\) | \(+\) | ||||
| \(e^x\) | \(0\) | ↗ | \(1\) | ↗ | \(+\infty\) |
Relation avec la fonction logarithme népérien
La fonction exponentielle et la fonction logarithme népérien sont intimement liées. Elles forment ce qu’on appelle des fonctions réciproques.
Définition : Fonction réciproque
La fonction logarithme népérien, notée \(\ln\), est la fonction réciproque de la fonction exponentielle. Elle réalise une bijection de \(]0 ; +\infty[\) sur \(\mathbb{R}\).
Concrètement, cela signifie que les deux fonctions « s’annulent » mutuellement :
\[ \forall x > 0, \quad e^{\ln(x)} = x \]
Applications pratiques
Ces relations permettent de résoudre efficacement équations et inéquations exponentielles :
Résolution d’équation : Résoudre \(e^{2x-1} = 5\)
e^{2x-1} &= 5 \\
\ln(e^{2x-1}) &= \ln(5) \quad \text{(on applique ln des deux côtés)} \\
2x – 1 &= \ln(5) \\
2x &= \ln(5) + 1 \\
x &= \frac{\ln(5) + 1}{2}
\end{align*}
Résolution d’inéquation : Résoudre \(e^{3x+2} \geq e^{x-1}\)
e^{3x+2} &\geq e^{x-1} \\
3x + 2 &\geq x – 1 \quad \text{(car exp est croissante)} \\
2x &\geq -3 \\
x &\geq -\frac{3}{2}
\end{align*}
L’ensemble des solutions est donc \(S = \left[-\dfrac{3}{2} ; +\infty\right[\).
Applications concrètes et modélisations
La fonction exponentielle n’est pas qu’un objet mathématique abstrait. Elle apparaît naturellement dans de nombreux phénomènes réels où la vitesse de changement d’une quantité est proportionnelle à cette quantité elle-même.
Croissance de populations
Dans des conditions idéales (ressources illimitées, pas de prédateurs), une population bactérienne croît selon un modèle exponentiel. Si \(N(t)\) désigne le nombre de bactéries au temps \(t\) (en heures), on peut avoir :
où \(N_0\) est la population initiale et \(k\) est le taux de croissance.
Exemple : Une colonie compte initialement 1000 bactéries et double toutes les 3 heures. Combien y aura-t-il de bactéries après 12 heures ?
Puisque la population double toutes les 3 heures, on a \(N(3) = 2N_0\). Donc :
Après 12 heures :
Décroissance radioactive
Les substances radioactives se désintègrent selon une loi exponentielle décroissante. Si \(m(t)\) représente la masse restante au temps \(t\), on a :
où \(\lambda > 0\) est la constante de désintégration. La demi-vie \(t_{1/2}\) est le temps nécessaire pour que la moitié de la substance se désintègre : \(m(t_{1/2}) = \dfrac{m_0}{2}\).
Croissance économique et intérêts composés
Un capital \(C_0\) placé à un taux d’intérêt annuel \(r\) (en composition continue) évolue selon :
Exemple : Un capital de 10000 euros est placé à 3% par an en composition continue. Quelle est sa valeur après 20 ans ?
Erreurs fréquentes à éviter
Erreur n°1 : Confondre \(e^{x+y}\) et \(e^x + e^y\)
Faux : \(e^{x+y} = e^x + e^y\)
Vrai : \(e^{x+y} = e^x \times e^y\)
Exemple : \(e^{2+3} = e^5 \neq e^2 + e^3\)
Erreur n°2 : Oublier que l’exponentielle est toujours positive
L’équation \(e^x = -5\) n’a aucune solution car \(e^x > 0\) pour tout \(x\).
Erreur n°3 : Mal dériver une composée
Faux : \(\left(e^{3x^2}\right)’ = e^{6x}\)
Vrai : \(\left(e^{3x^2}\right)’ = 6x \times e^{3x^2}\)
Ne pas oublier de multiplier par la dérivée de l’exposant !
Erreur n°4 : Confondre \(e^{2x}\) et \(2e^x\)
Ces deux expressions sont différentes !
\(e^{2x} = \left(e^x\right)^2\) tandis que \(2e^x\) est le double de \(e^x\).
Erreur n°5 : Mauvaise application des propriétés de croissance
Quand on résout \(e^{2x-1} > 5\), il faut d’abord écrire 5 sous forme exponentielle :
\(e^{2x-1} > e^{\ln(5)} \implies 2x – 1 > \ln(5)\)
Conclusion : L’importance de la fonction exponentielle
La fonction exponentielle occupe une place centrale en mathématiques et dans les sciences. Sa propriété caractéristique d’être égale à sa propre dérivée en fait un outil indispensable pour modéliser une multitude de phénomènes naturels et économiques.
Nous avons vu que cette fonction possède des propriétés algébriques élégantes qui simplifient grandement les calculs, qu’elle est strictement croissante et strictement positive sur \(\mathbb{R}\), et qu’elle croît plus rapidement que n’importe quelle fonction polynomiale.
Les applications pratiques sont omniprésentes : croissance démographique, décroissance radioactive, calculs d’intérêts composés, circuits électriques, lois de probabilité, et bien d’autres domaines scientifiques et techniques. Maîtriser la fonction exponentielle est donc essentiel pour réussir non seulement en mathématiques, mais aussi dans de nombreuses disciplines scientifiques.
Points clés à retenir
- La fonction exponentielle est l’unique fonction vérifiant \(f’ = f\) et \(f(0) = 1\)
- Elle est strictement positive et strictement croissante sur \(\mathbb{R}\)
- Ses propriétés algébriques reproduisent celles des puissances
- Elle croît plus vite que toute fonction polynomiale
- Elle est la réciproque du logarithme népérien
- Sa dérivée est elle-même, et pour une composée : \((e^{u})’ = u’ \times e^{u}\)
Questions fréquemment posées (FAQ)
Quelle est la différence entre exp(x) et e^x ?
Il n’y a aucune différence : ce sont deux notations pour la même fonction. La notation \(\exp(x)\) est utilisée dans les définitions formelles et pour éviter toute ambiguïté dans les expressions complexes, tandis que \(e^x\) est plus compacte et met en évidence les propriétés algébriques.
Comment calculer e^x sans calculatrice ?
On peut utiliser le développement en série : \(e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + …\). Plus on prend de termes, plus l’approximation est précise. Par exemple, pour \(x = 1\), les cinq premiers termes donnent \(e \approx 1 + 1 + 0{,}5 + 0{,}167 + 0{,}042 = 2{,}709\), proche de la valeur exacte 2,718.
La fonction exponentielle peut-elle être négative ?
Non, jamais. Pour tout nombre réel \(x\), on a toujours \(e^x > 0\). C’est l’une des propriétés fondamentales de cette fonction. Cela signifie qu’une équation comme \(e^x = -3\) n’a aucune solution dans l’ensemble des nombres réels.
Comment résoudre une équation avec des exponentielles ?
Il existe plusieurs méthodes selon le type d’équation : (1) Si les deux membres ont la forme \(e^a = e^b\), alors \(a = b\) par injectivité. (2) Si l’équation contient \(e^x\) à différentes puissances comme \(e^{2x}\) et \(e^x\), on peut poser \(X = e^x\) (changement de variable). (3) Si l’équation est de la forme \(e^x = k\) avec \(k > 0\), alors \(x = \ln(k)\) par application du logarithme.
Quelle est la primitive de e^x ?
La primitive de \(e^x\) est elle-même : \(\int e^x \, dx = e^x + C\) où \(C\) est une constante. Plus généralement, la primitive de \(e^{ax}\) est \(\frac{1}{a}e^{ax} + C\) pour \(a \neq 0\). Cette propriété découle directement du fait que la dérivée de \(e^x\) est \(e^x\).
Quelle est la valeur exacte du nombre e ?
Le nombre \(e\) est un nombre irrationnel et même transcendant, ce qui signifie qu’on ne peut pas l’écrire sous forme de fraction ni comme racine d’un polynôme à coefficients entiers. Sa valeur approchée est \(e \approx 2{,}718281828459045…\) Les premières décimales se retiennent facilement : 2,7 1828 1828 (on remarque la répétition de « 1828 »).