Le théorème de Thalès représente l’un des piliers fondamentaux de la géométrie euclidienne. Enseigné dès la quatrième et approfondi en troisième, ce théorème établit une relation remarquable entre parallélisme et proportionnalité. Qu’il s’agisse de calculer la hauteur d’un bâtiment inaccessible ou de résoudre des problèmes complexes de navigation maritime, le théorème de Thalès trouve des applications concrètes dans de nombreux domaines scientifiques et techniques.
Dans cette leçon exhaustive, nous explorerons non seulement l’énoncé classique du théorème, mais aussi sa démonstration rigoureuse, sa réciproque, et ses multiples configurations géométriques. Vous découvrirez comment ce principe mathématique, attribué au philosophe grec Thalès de Milet, continue d’être un outil indispensable pour quiconque souhaite maîtriser la géométrie plane.
Histoire et Origine du Théorème de Thalès
Thalès de Milet, philosophe et mathématicien grec du sixième siècle avant notre ère, est traditionnellement associé à ce théorème géométrique majeur. Selon une légende rapportée par Plutarque, Thalès aurait réussi à mesurer la hauteur de la pyramide de Khéops en Égypte en comparant l’ombre de la pyramide à celle d’un bâton de hauteur connue, illustrant parfaitement le principe de proportionnalité.
Cependant, les historiens modernes remettent en question cette attribution directe. Des tablettes babyloniennes datant de plus de mille ans avant Thalès révèlent que ce principe géométrique était déjà connu. La première démonstration formelle apparaît dans les Éléments d’Euclide d’Alexandrie, trois siècles après Thalès.
Énoncé du Théorème de Thalès
Théorème de Thalès (Configuration triangulaire)
Soit un triangle \(ABC\) et deux points \(D\) et \(E\) tels que :
- \(D\) appartient à la droite \((AB)\)
- \(E\) appartient à la droite \((AC)\)
- La droite \((DE)\) est parallèle à la droite \((BC)\), noté \((DE) \parallel (BC)\)
Alors les rapports suivants sont égaux :
\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}
\]
Remarque importante : On peut également écrire ces égalités en inversant les rapports :
\frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE}
\]
Cette formulation exprime que les triangles semblables \(ABC\) et \(ADE\) ont leurs côtés correspondants proportionnels. Le coefficient de proportionnalité correspond au rapport d’homothétie entre les deux triangles.
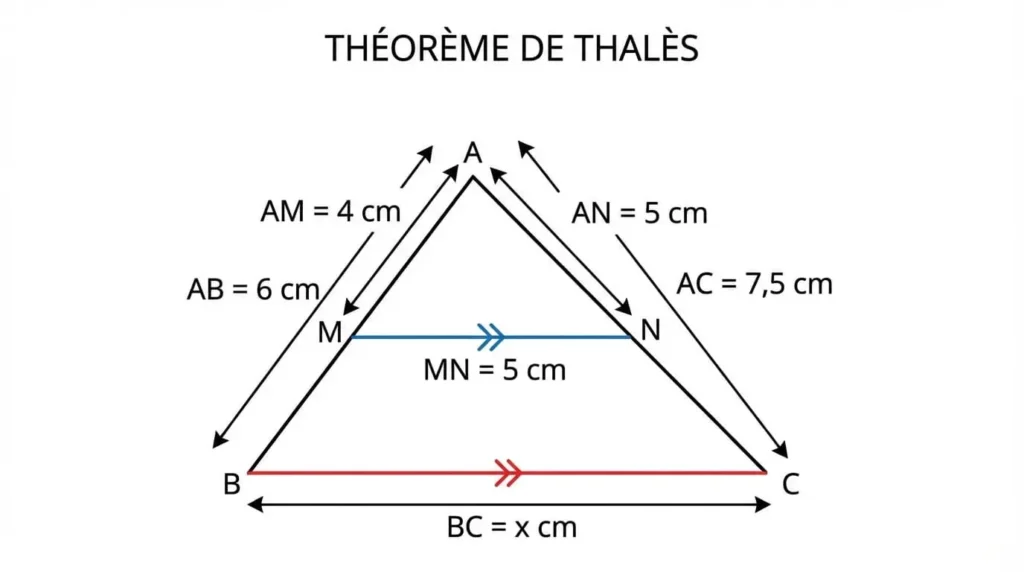
Configuration de Thalès : Les Cas Classiques
Le théorème de Thalès s’applique dans plusieurs configurations géométriques distinctes. Reconnaître ces configurations est essentiel pour appliquer correctement le théorème.
Première configuration : Triangles emboîtés
Dans cette configuration classique, les deux triangles partagent un sommet commun (point \(A\)) et sont disposés l’un dans l’autre. Le petit triangle \(ADE\) est emboîté dans le grand triangle \(ABC\). Les côtés \([DE]\) et \([BC]\) sont parallèles.
Caractéristiques :
- Les points \(A\), \(D\), \(B\) sont alignés dans cet ordre
- Les points \(A\), \(E\), \(C\) sont alignés dans cet ordre
- Le point \(A\) est à l’extérieur du segment \([DE]\)
- \((DE) \parallel (BC)\)
Deuxième configuration : Triangles en papillon
Dans cette configuration, le point d’intersection des droites sécantes se situe entre les deux droites parallèles. Les deux triangles forment une figure rappelant un papillon ou un nœud papillon.
Caractéristiques :
- Deux droites \((d_1)\) et \((d_2)\) se coupent en un point \(O\)
- Deux droites parallèles \((BC)\) et \((DE)\) coupent les droites sécantes
- Le point \(O\) se trouve entre les parallèles
- On obtient : \(\frac{OB}{OD} = \frac{OC}{OE} = \frac{BC}{DE}\)
Ordre des points et cohérence
Un aspect crucial souvent négligé concerne l’ordre des points dans les rapports. Pour que le théorème s’applique correctement, l’ordre d’énumération des points doit être cohérent sur les deux droites sécantes.
Attention : Si les points \(A\), \(D\), \(B\) sont alignés dans cet ordre, et les points \(A\), \(E\), \(C\) sont alignés dans cet ordre, alors vous devez respecter cet ordre dans vos rapports. Écrire \(\frac{AD}{AB}\) d’un côté et \(\frac{CA}{CE}\) de l’autre serait incorrect car l’ordre n’est pas respecté.
Démonstration Rigoureuse du Théorème
Plusieurs approches permettent de démontrer le théorème de Thalès. Nous présentons ici la démonstration d’Euclide, basée sur la comparaison des aires, puis une approche moderne utilisant les triangles semblables.
Démonstration par les aires (méthode d’Euclide)
Hypothèses :
- Triangle \(ABC\)
- Point \(D\) sur \([AB]\) et point \(E\) sur \([AC]\)
- \((DE) \parallel (BC)\)
Objectif : Démontrer que \(\frac{AD}{AB} = \frac{AE}{AC}\)
Démonstration :
Considérons les triangles \(BDE\) et \(CDE\). Ces deux triangles ont une base commune, le segment \([DE]\), et leurs sommets opposés \(B\) et \(C\) se trouvent sur une droite parallèle à cette base.
D’après une propriété fondamentale, deux triangles ayant la même base et dont les sommets se trouvent sur une parallèle à cette base ont la même aire. Donc :
\mathcal{A}(BDE) = \mathcal{A}(CDE)
\]
Maintenant, exprimons les aires des triangles \(ABE\) et \(ACD\) en fonction des précédentes :
\begin{align*}
\mathcal{A}(ABE) &= \mathcal{A}(ADE) + \mathcal{A}(BDE) \\
\mathcal{A}(ACD) &= \mathcal{A}(ADE) + \mathcal{A}(CDE)
\end{align*}
\]
Puisque \(\mathcal{A}(BDE) = \mathcal{A}(CDE)\), nous obtenons :
\mathcal{A}(ABE) = \mathcal{A}(ACD)
\]
Or, les triangles \(ABE\) et \(ADE\) partagent le même sommet \(E\) et ont leurs bases \([AB]\) et \([AD]\) sur la même droite. Le rapport de leurs aires est donc égal au rapport de leurs bases :
\frac{\mathcal{A}(ABE)}{\mathcal{A}(ADE)} = \frac{AB}{AD}
\]
De même, pour les triangles \(ACD\) et \(ADE\) :
\frac{\mathcal{A}(ACD)}{\mathcal{A}(ADE)} = \frac{AC}{AE}
\]
Puisque \(\mathcal{A}(ABE) = \mathcal{A}(ACD)\), nous avons :
\frac{AB}{AD} = \frac{AC}{AE}
\]
En inversant ces rapports, nous obtenons le résultat souhaité :
\frac{AD}{AB} = \frac{AE}{AC}
\]
Approche par les triangles semblables
Une méthode alternative, plus moderne, utilise la notion de similitude. Deux triangles sont semblables lorsque leurs angles correspondants sont égaux.
Dans notre configuration, puisque \((DE) \parallel (BC)\), nous avons :
- \(\widehat{ADE} = \widehat{ABC}\) (angles correspondants)
- \(\widehat{AED} = \widehat{ACB}\) (angles correspondants)
- \(\widehat{DAE} = \widehat{BAC}\) (angle commun)
Les triangles \(ADE\) et \(ABC\) ont donc leurs trois angles respectivement égaux : ils sont semblables. Cette similitude implique la proportionnalité de leurs côtés correspondants, ce qui démontre le théorème.
Applications et Calcul de Longueurs
Le théorème de Thalès trouve son application principale dans le calcul de longueurs inaccessibles ou inconnues. La méthode consiste à identifier une configuration de Thalès, à écrire les rapports égaux, puis à résoudre une équation de proportionnalité.
Méthodologie générale
Étapes pour calculer une longueur avec le théorème de Thalès :
- Identifier la configuration : Vérifiez la présence de deux droites parallèles coupées par deux sécantes
- Nommer les points : Repérez les points d’intersection et assurez-vous de l’alignement
- Énoncer le théorème : Précisez que vous appliquez le théorème de Thalès
- Écrire les rapports égaux : Formulez les trois rapports égaux
- Choisir le bon rapport : Sélectionnez celui contenant la longueur cherchée
- Remplacer par les valeurs : Substituez les longueurs connues
- Résoudre l’équation : Utilisez le produit en croix
- Conclure : Donnez le résultat avec l’unité
Exemple d’application pratique
Énoncé : Dans la figure ci-dessous, les droites \((MN)\) et \((BC)\) sont parallèles. On donne : \(AM = 4\) cm, \(AB = 7\) cm, \(AC = 10{,}5\) cm et \(MN = 6\) cm. Calculer les longueurs \(AN\) et \(BC\).
Solution détaillée :
Étape 1 : Identification
Les droites \((MN)\) et \((BC)\) sont parallèles. Les points \(A\), \(M\), \(B\) sont alignés, ainsi que les points \(A\), \(N\), \(C\). Nous sommes dans une configuration de Thalès avec triangles emboîtés.
Étape 2 : Énoncé
D’après le théorème de Thalès, nous avons :
\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}
\]
Étape 3 : Calcul de AN
Utilisons l’égalité \(\frac{AM}{AB} = \frac{AN}{AC}\) :
\begin{align*}
\frac{4}{7} &= \frac{AN}{10{,}5} \\
AN &= \frac{4 \times 10{,}5}{7} \\
AN &= \frac{42}{7} \\
AN &= 6 \text{ cm}
\end{align*}
\]
Étape 4 : Calcul de BC
Utilisons maintenant l’égalité \(\frac{AM}{AB} = \frac{MN}{BC}\) :
\begin{align*}
\frac{4}{7} &= \frac{6}{BC} \\
4 \times BC &= 6 \times 7 \\
4 \times BC &= 42 \\
BC &= \frac{42}{4} \\
BC &= 10{,}5 \text{ cm}
\end{align*}
\]
Conclusion : La longueur \(AN\) mesure 6 cm et la longueur \(BC\) mesure 10,5 cm.
Le cas particulier : théorème de la droite des milieux
Un cas particulier important du théorème de Thalès concerne les milieux de deux côtés d’un triangle.
Théorème de la droite des milieux
Dans un triangle, si une droite passe par les milieux de deux côtés, alors :
- Cette droite est parallèle au troisième côté
- La longueur du segment joignant ces deux milieux est égale à la moitié de la longueur du troisième côté
Formulation mathématique : Si \(I\) est le milieu de \([AB]\) et \(J\) est le milieu de \([AC]\), alors \((IJ) \parallel (BC)\) et \(IJ = \frac{BC}{2}\).
Ce théorème découle directement du théorème de Thalès en prenant \(\frac{AD}{AB} = \frac{1}{2}\), ce qui entraîne \(\frac{AE}{AC} = \frac{1}{2}\) et \(\frac{DE}{BC} = \frac{1}{2}\).
Réciproque du Théorème de Thalès
La réciproque du théorème de Thalès permet de démontrer que deux droites sont parallèles en vérifiant une égalité de rapports. C’est un outil fondamental dans les démonstrations géométriques.
Énoncé de la réciproque
Soit un triangle \(ABC\) et deux points \(M\) et \(N\) tels que :
- \(M\) appartient à la droite \((AB)\)
- \(N\) appartient à la droite \((AC)\)
- Les points \(A\), \(M\), \(B\) sont alignés dans le même ordre que \(A\), \(N\), \(C\)
Si l’égalité suivante est vérifiée :
\frac{AM}{AB} = \frac{AN}{AC}
\]
Alors les droites \((MN)\) et \((BC)\) sont parallèles : \((MN) \parallel (BC)\).
Méthode d’application de la réciproque
Démarche pour démontrer un parallélisme :
- Vérifier l’alignement : Assurez-vous que les points sont alignés dans le bon ordre
- Calculer les rapports : Calculez séparément \(\frac{AM}{AB}\) et \(\frac{AN}{AC}\)
- Comparer les rapports : Vérifiez si les deux rapports sont égaux
- Conclure : Si les rapports sont égaux, appliquez la réciproque pour conclure au parallélisme
Exemple d’utilisation de la réciproque
Énoncé : On considère un triangle \(ABC\) avec \(AB = 8\) cm et \(AC = 6\) cm. Un point \(M\) est placé sur \([AB]\) tel que \(AM = 5\) cm. Un point \(N\) est placé sur \([AC]\) tel que \(AN = 3{,}75\) cm. Les droites \((MN)\) et \((BC)\) sont-elles parallèles ?
Solution :
Étape 1 : Vérification des conditions
Les points \(A\), \(M\), \(B\) sont alignés dans cet ordre (car \(M \in [AB]\)). Les points \(A\), \(N\), \(C\) sont alignés dans cet ordre (car \(N \in [AC]\)). Les conditions d’alignement sont vérifiées.
Étape 2 : Calcul des rapports
\begin{align*}
\frac{AM}{AB} &= \frac{5}{8} = 0{,}625 \\
\frac{AN}{AC} &= \frac{3{,}75}{6} = \frac{3{,}75}{6} = 0{,}625
\end{align*}
\]
Étape 3 : Conclusion
Puisque \(\frac{AM}{AB} = \frac{AN}{AC}\) et que les points sont alignés dans le même ordre, d’après la réciproque du théorème de Thalès, les droites \((MN)\) et \((BC)\) sont parallèles.
Piège fréquent : Il ne suffit pas que les rapports soient égaux. L’ordre d’alignement des points doit impérativement être vérifié. Si \(M\) est sur le prolongement de \([AB]\) au-delà de \(B\), la réciproque ne s’applique pas directement.
Contraposée et Démonstrations de Non-Parallélisme
La contraposée du théorème de Thalès permet de démontrer que deux droites ne sont pas parallèles lorsque les rapports ne sont pas égaux.
Énoncé de la contraposée
Si les points \(A\), \(M\), \(B\) et \(A\), \(N\), \(C\) sont alignés dans le même ordre, et si :
\frac{AM}{AB} \neq \frac{AN}{AC}
\]
Alors les droites \((MN)\) et \((BC)\) ne sont pas parallèles.
Exemple de démonstration par la contraposée
Énoncé : Dans la figure suivante, les points \(T\), \(G\), \(L\) sont alignés et les points \(T\), \(F\), \(P\) sont alignés. On donne : \(TG = 3\) cm, \(TL = 10\) cm, \(TF = 1\) cm et \(TP = 3\) cm. Les droites \((FG)\) et \((LP)\) sont-elles parallèles ?
Solution :
Calculons les rapports :
\begin{align*}
\frac{TG}{TL} &= \frac{3}{10} = 0{,}3 \\
\frac{TF}{TP} &= \frac{1}{3} \approx 0{,}333…
\end{align*}
\]
Puisque \(\frac{3}{10} \neq \frac{1}{3}\), nous avons \(\frac{TG}{TL} \neq \frac{TF}{TP}\).
Les points sont alignés dans le même ordre, mais les rapports sont différents. D’après la contraposée du théorème de Thalès, les droites \((FG)\) et \((LP)\) ne sont pas parallèles.
Exercices Corrigés Étape par Étape
Exercice 1 : Configuration classique
Énoncé : Dans le triangle \(DEF\), on place un point \(G\) sur \([DE]\) et un point \(H\) sur \([DF]\) tels que \((GH) \parallel (EF)\). On sait que \(DG = 4\) cm, \(DE = 12\) cm et \(EF = 9\) cm. Calculer \(GH\).
Solution :
Puisque \((GH) \parallel (EF)\), d’après le théorème de Thalès :
\frac{DG}{DE} = \frac{DH}{DF} = \frac{GH}{EF}
\]
Utilisons \(\frac{DG}{DE} = \frac{GH}{EF}\) :
\begin{align*}
\frac{4}{12} &= \frac{GH}{9} \\
GH &= \frac{4 \times 9}{12} \\
GH &= \frac{36}{12} \\
GH &= 3 \text{ cm}
\end{align*}
\]
Réponse : La longueur \(GH\) mesure 3 cm.
Exercice 2 : Configuration papillon
Énoncé : Deux droites \((d)\) et \((d’)\) se coupent en \(O\). Deux droites parallèles coupent \((d)\) en \(A\) et \(B\), et \((d’)\) en \(C\) et \(D\). On donne : \(OA = 5\) cm, \(AB = 3\) cm, \(OC = 7\) cm. Calculer \(CD\).
Solution :
Dans une configuration papillon avec \((AC) \parallel (BD)\), le théorème de Thalès s’écrit :
\frac{OA}{OB} = \frac{OC}{OD}
\]
Nous avons \(OB = OA + AB = 5 + 3 = 8\) cm.
Calculons \(OD\) :
\begin{align*}
\frac{5}{8} &= \frac{7}{OD} \\
5 \times OD &= 7 \times 8 \\
OD &= \frac{56}{5} \\
OD &= 11{,}2 \text{ cm}
\end{align*}
\]
Donc \(CD = OD – OC = 11{,}2 – 7 = 4{,}2\) cm.
Réponse : La longueur \(CD\) mesure 4,2 cm.
Exercice 3 : Application de la réciproque
Énoncé : Dans un triangle \(RST\), on place \(U\) sur \([RS]\) et \(V\) sur \([RT]\). On mesure : \(RU = 6\) cm, \(RS = 15\) cm, \(RV = 4\) cm, \(RT = 10\) cm. Démontrer que \((UV) \parallel (ST)\).
Solution :
Les points \(R\), \(U\), \(S\) sont alignés dans cet ordre, et les points \(R\), \(V\), \(T\) sont alignés dans cet ordre. Calculons les rapports :
\begin{align*}
\frac{RU}{RS} &= \frac{6}{15} = \frac{2}{5} = 0{,}4 \\
\frac{RV}{RT} &= \frac{4}{10} = \frac{2}{5} = 0{,}4
\end{align*}
\]
Puisque \(\frac{RU}{RS} = \frac{RV}{RT}\) et que les points sont alignés dans le même ordre, d’après la réciproque du théorème de Thalès, les droites \((UV)\) et \((ST)\) sont parallèles.
Exercice 4 : Problème avec calcul littéral
Énoncé : Dans un triangle \(ABC\), un point \(M\) est sur \([AB]\) tel que \(AM = x\) et \(MB = 2x\). Un point \(N\) est sur \([AC]\) tel que \(AN = 5\) cm. On sait que \((MN) \parallel (BC)\). Calculer \(AC\) en fonction de \(x\).
Solution :
Nous avons \(AB = AM + MB = x + 2x = 3x\).
D’après le théorème de Thalès :
\begin{align*}
\frac{AM}{AB} &= \frac{AN}{AC} \\
\frac{x}{3x} &= \frac{5}{AC} \\
\frac{1}{3} &= \frac{5}{AC} \\
AC &= 5 \times 3 \\
AC &= 15 \text{ cm}
\end{align*}
\]
Réponse : Quelle que soit la valeur de \(x\) (pourvu que \(x > 0\)), la longueur \(AC\) mesure 15 cm.
Exercice 5 : Problème contextualisé
Énoncé : Un arbre projette une ombre de 12 mètres au sol. Au même moment, un bâton vertical de 1,5 m projette une ombre de 2 m. Quelle est la hauteur de l’arbre ?
Solution :
Les rayons du soleil sont parallèles. Cette situation crée deux triangles semblables : celui formé par l’arbre et son ombre, et celui formé par le bâton et son ombre.
Par proportionnalité (application du théorème de Thalès) :
\frac{\text{Hauteur arbre}}{\text{Ombre arbre}} = \frac{\text{Hauteur bâton}}{\text{Ombre bâton}}
\]
Notons \(h\) la hauteur de l’arbre :
\begin{align*}
\frac{h}{12} &= \frac{1{,}5}{2} \\
h &= \frac{1{,}5 \times 12}{2} \\
h &= \frac{18}{2} \\
h &= 9 \text{ m}
\end{align*}
\]
Réponse : L’arbre mesure 9 mètres de hauteur. C’est exactement la méthode attribuée à Thalès pour mesurer la pyramide de Khéops !
Conclusion
Le théorème de Thalès constitue une pierre angulaire de la géométrie euclidienne. Sa compréhension permet non seulement de résoudre des problèmes de calcul de longueurs, mais ouvre également la voie à des concepts plus avancés comme les homothéties, les similitudes et les transformations géométriques.
Points essentiels à retenir :
- Le théorème établit une proportionnalité entre segments lorsque des droites parallèles coupent deux sécantes
- La configuration triangulaire emboîtée est la plus courante, mais la configuration papillon existe aussi
- L’ordre des points dans les rapports doit être strictement respecté
- La réciproque permet de démontrer qu’un parallélisme existe en vérifiant l’égalité des rapports
- La contraposée permet de prouver l’absence de parallélisme par l’inégalité des rapports
- Le théorème trouve de nombreuses applications pratiques dans divers domaines scientifiques et techniques
Pour maîtriser parfaitement ce théorème, la pratique régulière d’exercices variés est indispensable. N’hésitez pas à dessiner des figures, à identifier les configurations et à rédiger soigneusement vos démonstrations en justifiant chaque étape.