Définition et Notion Intuitive d’Intégrale
Qu’est-ce qu’une intégrale ?
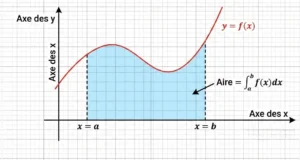
L’intégrale d’une fonction représente fondamentalement l’aire délimitée par la courbe représentative de cette fonction, l’axe des abscisses et deux droites verticales. Cette interprétation géométrique constitue le point de départ pour comprendre le concept d’intégration.
Définition : Intégrale d’une fonction continue positive
Soit \( f \) une fonction continue et positive sur un intervalle \([a ; b]\). On appelle intégrale de \( f \) sur \([a ; b]\) l’aire, exprimée en unités d’aire, du domaine délimité par la courbe représentative de \( f \), l’axe des abscisses, et les droites d’équations \( x = a \) et \( x = b \).
Cette notation se lit : « intégrale de a à b de f de x dx ». Les nombres \( a \) et \( b \) sont appelés les bornes de l’intégrale, respectivement borne inférieure et borne supérieure.
Unité d’aire et calcul d’aires géométriques
Dans un repère orthonormé, le rectangle unité de dimensions 1 sur 1 possède une aire de 1 unité d’aire (notée 1 u.a.). Cette unité fondamentale permet de mesurer toutes les autres aires. Pour les figures géométriques simples comme les rectangles, triangles ou trapèzes, le calcul de l’aire sous une courbe peut se faire directement par des formules géométriques classiques.
Extension aux fonctions négatives
Lorsqu’une fonction prend des valeurs négatives sur un intervalle, l’intégrale correspond à une aire algébrique : les portions situées au-dessus de l’axe des abscisses contribuent positivement, tandis que celles situées en dessous contribuent négativement.
Intégrale d’une fonction négative
Soit \( f \) une fonction continue et négative sur \([a ; b]\). L’aire du domaine délimité par la courbe de \( f \), l’axe des abscisses et les droites \( x = a \) et \( x = b \) vaut :
Primitives de Fonctions : Concept Fondamental
Définition d’une primitive
La notion de primitive représente l’opération inverse de la dérivation. Elle joue un rôle central dans le calcul des intégrales grâce au théorème fondamental de l’analyse.
Primitive d’une fonction
Soit \( f \) une fonction définie sur un intervalle \( I \). On dit qu’une fonction \( F \) est une primitive de \( f \) sur \( I \) si \( F \) est dérivable sur \( I \) et si pour tout \( x \) appartenant à \( I \) :
Non-unicité des primitives
Théorème : Ensemble des primitives
Si \( F \) est une primitive de \( f \) sur un intervalle \( I \), alors toutes les primitives de \( f \) sur \( I \) sont de la forme \( F(x) + C \), où \( C \) est une constante réelle quelconque.
Réciproquement, deux primitives d’une même fonction sur un intervalle diffèrent d’une constante.
Exemple : Les primitives de \( f(x) = 2x \) sont toutes les fonctions de la forme \( F(x) = x^2 + C \), où \( C \in \mathbb{R} \).
Tableau des primitives usuelles
Pour calculer efficacement des intégrales, il est essentiel de connaître les primitives des fonctions usuelles. Voici un tableau récapitulatif des primitives les plus fréquentes :
| Fonction \( f(x) \) | Primitive \( F(x) \) (à une constante près) | Intervalle de validité |
|---|---|---|
| \( k \) (constante) | \( kx \) | \( \mathbb{R} \) |
| \( x^n \) avec \( n \neq -1 \) | \( \dfrac{x^{n+1}}{n+1} \) | \( \mathbb{R} \) si \( n \in \mathbb{N} \), \( \mathbb{R}^* \) sinon |
| \( \dfrac{1}{x} \) | \( \ln|x| \) | \( \mathbb{R}^* \) |
| \( e^x \) | \( e^x \) | \( \mathbb{R} \) |
| \( \cos(x) \) | \( \sin(x) \) | \( \mathbb{R} \) |
| \( \sin(x) \) | \( -\cos(x) \) | \( \mathbb{R} \) |
| \( \dfrac{1}{1+x^2} \) | \( \arctan(x) \) | \( \mathbb{R} \) |
| \( \dfrac{1}{\sqrt{1-x^2}} \) | \( \arcsin(x) \) | \( ]-1 ; 1[ \) |
Primitives de fonctions composées
Pour les fonctions composées de la forme \( u'(x) \times f(u(x)) \), si \( F \) est une primitive de \( f \), alors une primitive est \( F(u(x)) \).
Exemple : Pour calculer une primitive de \( 2x \cos(x^2) \), on reconnaît la forme \( u'(x) \times \cos(u(x)) \) avec \( u(x) = x^2 \) et \( u'(x) = 2x \). Une primitive est donc \( \sin(x^2) \).
Théorème Fondamental de l’Analyse
Le théorème fondamental du calcul intégral établit le lien profond entre les deux opérations fondamentales de l’analyse : la dérivation et l’intégration. Ce théorème révolutionnaire, développé par Newton et Leibniz au XVIIe siècle, a transformé notre capacité à calculer des aires et à résoudre des problèmes en physique et en mathématiques.
Théorème fondamental du calcul intégral (Première partie)
Soit \( f \) une fonction continue sur un intervalle \( I \) et \( a \) un élément de \( I \). La fonction \( F \) définie sur \( I \) par :
est dérivable sur \( I \) et constitue l’unique primitive de \( f \) qui s’annule en \( a \). De plus, pour tout \( x \in I \) :
Cette première partie affirme qu’en dérivant une fonction aire, on retrouve la fonction intégrée. Elle garantit également l’existence de primitives pour toute fonction continue.
Théorème fondamental du calcul intégral (Seconde partie)
Soit \( f \) une fonction continue sur un intervalle \([a ; b]\) et \( F \) une primitive quelconque de \( f \) sur cet intervalle. Alors :
On note également : \( \int_{a}^{b} f(x) \, dx = [F(x)]_{a}^{b} \)
Cette seconde partie fournit une méthode pratique pour calculer des intégrales : il suffit de trouver une primitive et d’évaluer sa différence aux bornes.
Exemple d’application : Calculons \( \int_{0}^{1} 2x \, dx \).
Une primitive de \( f(x) = 2x \) est \( F(x) = x^2 \). Donc :
\begin{align*}
\int_{0}^{1} 2x \, dx &= [x^2]_{0}^{1} \\
&= 1^2 – 0^2 \\
&= 1
\end{align*}
\]
Propriétés Algébriques des Intégrales
Le calcul intégral possède de nombreuses propriétés qui simplifient considérablement les calculs et permettent de décomposer des intégrales complexes en tâches plus élémentaires.
Linéarité de l’intégrale
Propriété : Linéarité
Soient \( f \) et \( g \) deux fonctions continues sur \([a ; b]\) et \( \lambda, \mu \) deux nombres réels. Alors :
Relation de Chasles
Relation de Chasles
Soit \( f \) une fonction continue sur un intervalle \( I \) et \( a, b, c \) trois réels de \( I \). Alors :
Cette propriété permet de découper une intégrale en plusieurs morceaux, particulièrement utile lorsque la fonction change de signe ou de formule sur l’intervalle.
Propriété de symétrie
En particulier, \( \int_{a}^{a} f(x) \, dx = 0 \)
Positivité et ordre
Propriété : Positivité
Si \( f \) est une fonction continue sur \([a ; b]\) telle que \( f(x) \geq 0 \) pour tout \( x \in [a ; b] \), alors :
Propriété : Ordre
Si \( f \) et \( g \) sont deux fonctions continues sur \([a ; b]\) telles que \( f(x) \leq g(x) \) pour tout \( x \in [a ; b] \), alors :
Intégrales de fonctions paires et impaires
Ces propriétés permettent souvent de simplifier considérablement les calculs lorsque l’intervalle d’intégration est symétrique par rapport à zéro.
- Fonction paire : Si \( f \) est paire et continue sur \([-a ; a]\), alors \( \int_{-a}^{a} f(x) \, dx = 2\int_{0}^{a} f(x) \, dx \)
- Fonction impaire : Si \( f \) est impaire et continue sur \([-a ; a]\), alors \( \int_{-a}^{a} f(x) \, dx = 0 \)
Techniques Avancées de Calcul d’Intégrales
Intégration par parties
L’intégration par parties est une technique fondamentale qui transforme l’intégrale d’un produit de fonctions en une forme plus simple. Elle dérive directement de la formule de dérivation d’un produit.
Formule d’intégration par parties
Soient \( u \) et \( v \) deux fonctions dérivables de classe \( \mathcal{C}^1 \) sur \([a ; b]\). Alors :
Ou de manière équivalente :
Méthode ALPES pour le choix des fonctions
Pour appliquer efficacement l’intégration par parties, il faut choisir judicieusement quelle fonction dériver et laquelle intégrer. La méthode mnémotechnique ALPES indique l’ordre de priorité pour choisir la fonction à dériver :
- A : Fonctions Arc (arctan, arcsin, arccos)
- L : Logarithmes (ln, log)
- P : Polynômes
- E : Exponentielles
- S : Sinus et cosinus
La fonction qui apparaît en premier dans cette liste doit être choisie comme \( u \) (à dériver).
Exemple résolu : Calcul de \( \int_{0}^{1} x e^x \, dx \)
Appliquons la méthode ALPES : nous avons un polynôme \( x \) et une exponentielle \( e^x \). Le polynôme vient avant l’exponentielle dans ALPES, donc on pose :
- \( u(x) = x \) donc \( u'(x) = 1 \)
- \( v'(x) = e^x \) donc \( v(x) = e^x \)
\begin{align*}
\int_{0}^{1} x e^x \, dx &= [x e^x]_{0}^{1} – \int_{0}^{1} 1 \cdot e^x \, dx \\
&= (1 \cdot e^1 – 0 \cdot e^0) – [e^x]_{0}^{1} \\
&= e – (e – 1) \\
&= 1
\end{align*}
\]
Intégrations par parties successives
Certaines intégrales nécessitent plusieurs applications successives de la formule. C’est notamment le cas pour les produits de polynômes de degré élevé avec des exponentielles ou des fonctions trigonométriques.
Exemple : Pour \( \int_{0}^{1} x^2 e^x \, dx \), on applique deux fois l’intégration par parties pour diminuer progressivement le degré du polynôme.
Changement de variable
Le changement de variable est une technique qui consiste à substituer la variable d’intégration par une nouvelle variable, transformant ainsi l’intégrale en une forme plus facile à calculer.
Formule de changement de variable
Soit \( \varphi \) une fonction de classe \( \mathcal{C}^1 \) sur un intervalle \([α ; β]\) et \( f \) une fonction continue sur \( \varphi([α ; β]) \). Alors :
Exemple : Calculons \( \int_{0}^{1} 2x\sqrt{1+x^2} \, dx \) par changement de variable.
Posons \( u = 1 + x^2 \), alors \( du = 2x \, dx \). Les bornes deviennent : pour \( x = 0 \), \( u = 1 \) ; pour \( x = 1 \), \( u = 2 \).
\begin{align*}
\int_{0}^{1} 2x\sqrt{1+x^2} \, dx &= \int_{1}^{2} \sqrt{u} \, du \\
&= \left[\frac{2}{3}u^{3/2}\right]_{1}^{2} \\
&= \frac{2}{3}(2^{3/2} – 1) \\
&= \frac{2}{3}(2\sqrt{2} – 1)
\end{align*}
\]
Applications du Calcul Intégral
Calcul d’aires
L’application la plus directe du calcul intégral consiste à déterminer des aires de domaines plans délimités par des courbes.
Aire entre une courbe et l’axe des abscisses
Pour une fonction \( f \) continue sur \([a ; b]\) :
- Si \( f \geq 0 \) sur \([a ; b]\), l’aire vaut \( \int_{a}^{b} f(x) \, dx \)
- Si \( f \leq 0 \) sur \([a ; b]\), l’aire vaut \( -\int_{a}^{b} f(x) \, dx = \int_{a}^{b} |f(x)| \, dx \)
- Si \( f \) change de signe, on décompose l’intervalle selon les zéros de \( f \)
Aire entre deux courbes
L’aire du domaine compris entre les courbes de deux fonctions \( f \) et \( g \) continues sur \([a ; b]\), avec \( f(x) \geq g(x) \) pour tout \( x \in [a ; b] \), est donnée par :
Valeur moyenne d’une fonction
Le calcul intégral permet de définir rigoureusement la notion de valeur moyenne d’une fonction sur un intervalle, généralisant la notion de moyenne arithmétique.
Valeur moyenne
Soit \( f \) une fonction continue sur \([a ; b]\). La valeur moyenne de \( f \) sur cet intervalle est le nombre réel :
Géométriquement, la valeur moyenne représente la hauteur du rectangle de base \([a ; b]\) ayant la même aire que le domaine sous la courbe de \( f \).
Exercices corrigés et Méthodes
Exercice 1 : Calcul direct avec une primitive
Énoncé : Calculer \( \int_{1}^{e} \frac{1}{x} \, dx \)
Solution :
La fonction \( f(x) = \frac{1}{x} \) est continue sur \([1 ; e]\). Une primitive de \( f \) est \( F(x) = \ln|x| = \ln(x) \) car \( x > 0 \) sur l’intervalle.
\begin{align*}
\int_{1}^{e} \frac{1}{x} \, dx &= [\ln(x)]_{1}^{e} \\
&= \ln(e) – \ln(1) \\
&= 1 – 0 \\
&= 1
\end{align*}
\]
Exercice 2 : Utilisation de la linéarité
Énoncé : Calculer \( \int_{0}^{\pi} (3\cos(x) – 2\sin(x)) \, dx \)
Solution :
Par linéarité de l’intégrale :
\begin{align*}
\int_{0}^{\pi} (3\cos(x) – 2\sin(x)) \, dx &= 3\int_{0}^{\pi} \cos(x) \, dx – 2\int_{0}^{\pi} \sin(x) \, dx \\
&= 3[\sin(x)]_{0}^{\pi} – 2[-\cos(x)]_{0}^{\pi} \\
&= 3(\sin(\pi) – \sin(0)) + 2(\cos(\pi) – \cos(0)) \\
&= 3(0 – 0) + 2(-1 – 1) \\
&= 0 – 4 \\
&= -4
\end{align*}
\]
Exercice 3 : Relation de Chasles
Énoncé : Sachant que \( \int_{0}^{2} f(x) \, dx = 5 \) et \( \int_{0}^{5} f(x) \, dx = 12 \), calculer \( \int_{2}^{5} f(x) \, dx \)
Solution :
D’après la relation de Chasles : \( \int_{0}^{5} f(x) \, dx = \int_{0}^{2} f(x) \, dx + \int_{2}^{5} f(x) \, dx \)
Donc : \( \int_{2}^{5} f(x) \, dx = \int_{0}^{5} f(x) \, dx – \int_{0}^{2} f(x) \, dx = 12 – 5 = 7 \)
Exercice 4 : Intégration par parties
Énoncé : Calculer \( \int_{1}^{e} \ln(x) \, dx \)
Solution :
Nous avons une fonction logarithme seule. On utilise l’intégration par parties avec :
- \( u(x) = \ln(x) \) donc \( u'(x) = \frac{1}{x} \)
- \( v'(x) = 1 \) donc \( v(x) = x \)
\begin{align*}
\int_{1}^{e} \ln(x) \, dx &= [x\ln(x)]_{1}^{e} – \int_{1}^{e} x \cdot \frac{1}{x} \, dx \\
&= [x\ln(x)]_{1}^{e} – \int_{1}^{e} 1 \, dx \\
&= (e\ln(e) – 1\ln(1)) – [x]_{1}^{e} \\
&= (e \cdot 1 – 1 \cdot 0) – (e – 1) \\
&= e – e + 1 \\
&= 1
\end{align*}
\]
Exercice 5 : Changement de variable
Énoncé : Calculer \( \int_{0}^{\pi/2} \sin(x)\cos(x) \, dx \)
Solution :
Posons \( u = \sin(x) \), alors \( du = \cos(x) \, dx \). Les bornes : pour \( x = 0 \), \( u = 0 \) ; pour \( x = \frac{\pi}{2} \), \( u = 1 \).
\begin{align*}
\int_{0}^{\pi/2} \sin(x)\cos(x) \, dx &= \int_{0}^{1} u \, du \\
&= \left[\frac{u^2}{2}\right]_{0}^{1} \\
&= \frac{1}{2} – 0 \\
&= \frac{1}{2}
\end{align*}
\]
Conclusion et Résumé
Le calcul intégral représente l’un des outils mathématiques les plus puissants et les plus utilisés dans les sciences. À travers ce cours complet, nous avons exploré les concepts fondamentaux qui permettent de maîtriser cette discipline essentielle.
Les points clés à retenir :
- L’intégrale mesure l’aire sous une courbe et généralise la notion d’accumulation de quantités infinitésimales
- Une primitive d’une fonction \( f \) est une fonction \( F \) dont la dérivée est \( f \). Toutes les primitives d’une même fonction diffèrent d’une constante
- Le théorème fondamental du calcul intégral établit le lien entre dérivation et intégration, permettant de calculer des intégrales via les primitives : \( \int_{a}^{b} f(x) \, dx = F(b) – F(a) \)
- Les propriétés algébriques (linéarité, relation de Chasles, positivité) simplifient considérablement les calculs d’intégrales
- Les techniques avancées comme l’intégration par parties et le changement de variable permettent de résoudre des intégrales complexes
- Les applications pratiques du calcul intégral sont innombrables : calcul d’aires, de volumes, de valeurs moyennes, résolution de problèmes physiques
- Pour approfondir, consultez le cours complet sur les intégrales généralisées ou intégrale de riemann.
La maîtrise du calcul intégral nécessite de la pratique régulière. Familiarisez-vous avec le tableau des primitives usuelles, entraînez-vous sur des exercices variés, et n’hésitez pas à décomposer les problèmes complexes en étapes plus simples. Avec le temps et la persévérance, les techniques d’intégration deviendront des outils naturels dans votre arsenal mathématique.
Questions Fréquemment Posées (FAQ)
Quelle est la différence entre primitive et intégrale ?
Une primitive est une fonction dont la dérivée est égale à la fonction de départ, tandis qu’une intégrale définie est un nombre représentant l’aire sous une courbe entre deux bornes. Mathématiquement, si \( F \) est une primitive de \( f \), alors \( F'(x) = f(x) \). L’intégrale définie utilise les primitives pour son calcul : \( \int_{a}^{b} f(x) \, dx = F(b) – F(a) \). En résumé : primitive = fonction, intégrale définie = nombre.
Comment calculer une intégrale sans primitive connue ?
Lorsque la primitive n’est pas immédiatement identifiable, plusieurs techniques s’offrent à vous : l’intégration par parties (pour les produits de fonctions), le changement de variable (pour simplifier l’expression), ou la décomposition en éléments simples (pour les fractions rationnelles). Il existe également des méthodes numériques d’approximation comme la méthode des rectangles ou la méthode de Simpson pour obtenir une valeur approchée quand aucune primitive analytique n’existe.
Pourquoi l’intégrale d’une fonction négative est négative ?
L’intégrale mesure une aire algébrique : les portions de courbe au-dessus de l’axe des abscisses contribuent positivement, celles en dessous contribuent négativement. Quand \( f(x) < 0 \) sur \([a ; b]\), la courbe est sous l’axe, donc l’intégrale \( \int_{a}^{b} f(x) \, dx \) est négative. Pour obtenir l’aire géométrique (toujours positive), on calcule \( \int_{a}^{b} |f(x)| \, dx \) ou \( -\int_{a}^{b} f(x) \, dx \) si \( f \) est négative sur tout l’intervalle.
Quand utiliser l’intégration par parties ?
L’intégration par parties s’utilise principalement pour intégrer un produit de deux fonctions, notamment quand l’une des fonctions se simplifie par dérivation. La méthode ALPES aide à choisir : on dérive en priorité les fonctions Arc (arctan, arcsin), puis Logarithmes, Polynômes, Exponentielles, et enfin Sinus/cosinus. Par exemple, pour \( \int x e^x \, dx \), on dérive le polynôme \( x \) et on intègre \( e^x \). Cette technique est particulièrement efficace pour les produits polynôme×exponentielle ou polynôme×trigonométrique.
Comment vérifier qu’un calcul d’intégrale est correct ?
Pour vérifier votre calcul d’intégrale, plusieurs méthodes existent : dérivez le résultat obtenu (la primitive) pour retrouver la fonction initiale ; vérifiez la cohérence des unités et du signe (une aire ne peut être négative que si c’est une aire algébrique) ; estimez graphiquement l’ordre de grandeur de l’aire ; utilisez les propriétés comme la linéarité ou la relation de Chasles pour décomposer le calcul différemment. Enfin, une calculatrice ou un logiciel de calcul formel peut servir de vérification finale.
Qu’est-ce que le théorème fondamental de l’analyse ?
Le théorème fondamental de l’analyse établit le lien essentiel entre dérivation et intégration. Il comporte deux parties : la première affirme que toute fonction continue admet des primitives et que la dérivée de l’intégrale \( F(x) = \int_{a}^{x} f(t) \, dt \) est la fonction \( f \) elle-même. La seconde partie donne la formule de calcul pratique : \( \int_{a}^{b} f(x) \, dx = F(b) – F(a) \) où \( F \) est une primitive de \( f \). Ce théorème révolutionnaire permet de calculer des aires sans passer par des sommes infinies.