La notion de produit scalaire est l’un des piliers de la géométrie vectorielle et analytique. Apparue initialement pour répondre aux besoins précis de la physique, cette opération mathématique permet de lier la géométrie pure (longueurs, angles) au calcul algébrique.
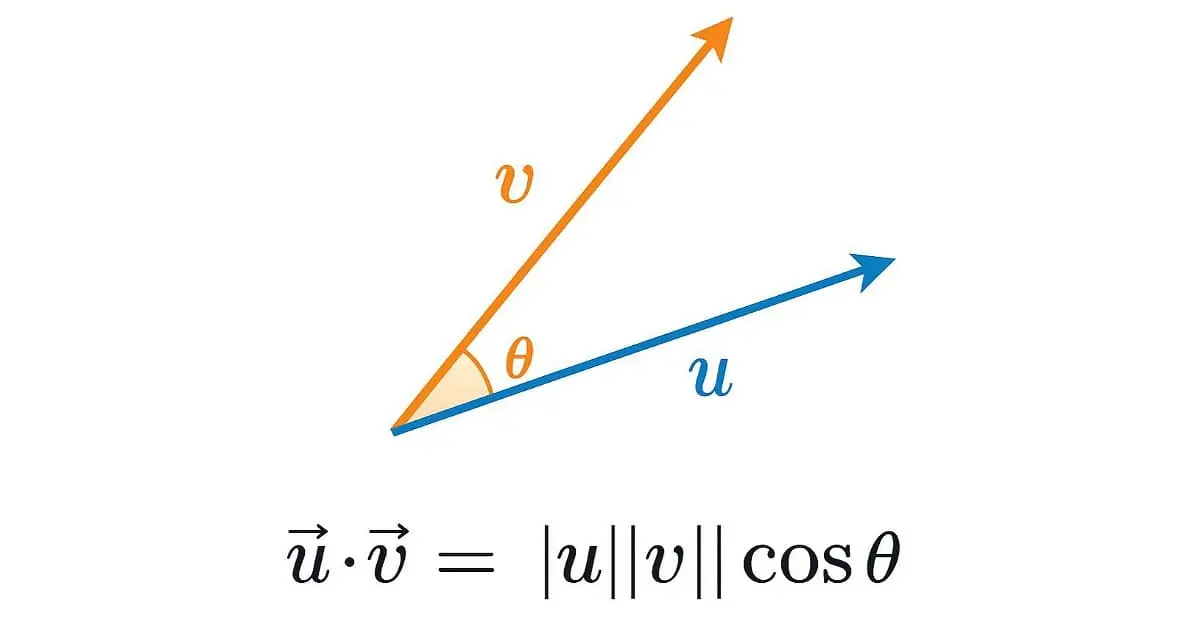
Dans ce cours complet sur le produit scalaire, nous allons explorer en profondeur comment calculer un produit scalaire, comprendre ses propriétés fondamentales, et l’appliquer à travers des théorèmes puissants comme celui d’Al Kashi. Que vous cherchiez une produit scalaire formule spécifique ou des exercices corrigés, ce guide couvre l’intégralité du programme. Contrairement aux opérations vectorielles classiques, le résultat ici est un nombre réel (un scalaire), d’où son nom.
Définition et Calcul du Produit Scalaire de Deux Vecteurs
Il existe plusieurs manières d’aborder le produit scalaire de deux vecteurs. Le choix de la méthode dépend essentiellement des informations dont vous disposez dans l’énoncé de votre problème : les normes (longueurs), les angles ou les coordonnées.
La Formule Géométrique (Norme et Cosinus)
C’est la définition la plus intuitive pour comprendre le sens physique du produit scalaire.
Définition : Produit scalaire de deux vecteurs
Soient deux vecteurs \( \vec{u} \) et \( \vec{v} \) du plan. On appelle produit scalaire de \( \vec{u} \) par \( \vec{v} \), noté \( \vec{u} \cdot \vec{v} \), le nombre réel défini par :
- Si l’un des vecteurs est nul (\( \vec{u} = \vec{0} \) ou \( \vec{v} = \vec{0} \)), alors : \( \vec{u} \cdot \vec{v} = 0 \)
- Sinon, la formule fondamentale est :\[ \vec{u} \cdot \vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times \cos(\vec{u}, \vec{v}) \]
⚠️ Attention aux notations : Le produit scalaire se note avec un point (\( \vec{u} \cdot \vec{v} \)) et se lit « u scalaire v ». Il ne faut jamais écrire \( \vec{u} \cdot \vec{v} = \vec{0} \) car le résultat est un nombre réel, pas un vecteur.
Interprétation du signe
Le signe du résultat dépend exclusivement de l’angle entre les vecteurs, car les normes \( ||\vec{u}|| \) et \( ||\vec{v}|| \) sont toujours positives :
- Si l’angle est aigu (entre 0° et 90°), le cosinus est positif, donc \( \vec{u} \cdot \vec{v} > 0 \).
- Si l’angle est obtus (entre 90° et 180°), le cosinus est négatif, donc \( \vec{u} \cdot \vec{v} < 0 \).
- Si \( \vec{u} \) et \( \vec{v} \) sont colinéaires de même sens : \( \vec{u} \cdot \vec{v} = ||\vec{u}|| \times ||\vec{v}|| \) (car \( \cos 0 = 1 \)).
- Si \( \vec{u} \) et \( \vec{v} \) sont colinéaires de sens contraires : \( \vec{u} \cdot \vec{v} = -||\vec{u}|| \times ||\vec{v}|| \) (car \( \cos \pi = -1 \)).
Soit un triangle équilatéral ABC de côté \( a \). Calculons \( \vec{AB} \cdot \vec{AC} \). L’angle \( \widehat{BAC} \) vaut \( 60^{\circ} \). En appliquant la formule :
Ce résultat standard est très utile dans les exercices.
Calcul par Projection Orthogonale
Parfois, les angles ne sont pas donnés explicitement, mais la configuration géométrique permet une approche par projection. Cette méthode est souvent plus rapide pour calculer un produit scalaire dans des figures comme les carrés ou les rectangles.
Définition : Projection orthogonale
Soient \( \vec{u} = \vec{OA} \) et \( \vec{v} = \vec{OB} \). Si \( H \) est le projeté orthogonal du point \( B \) sur la droite \( (OA) \), alors :
Si \( \vec{OA} \) et \( \vec{OH} \) sont dans le même sens, le produit est positif. S’ils sont de sens opposés, il est négatif.
Dans un carré ABCD de côté \( c \), calculons \( \vec{AB} \cdot \vec{AC} \). Le projeté orthogonal de C sur la droite (AB) est le point B lui-même. Donc :
Produit Scalaire en Coordonnées : La Méthode Analytique
Lorsque le plan est muni d’un repère orthonormé \( (O;\, \vec{i},\, \vec{j}) \), le calcul du produit scalaire devient purement algébrique, ce qui le rend extrêmement efficace.
Théorème : Formule analytique du produit scalaire
Si \( \vec{u} \) a pour coordonnées \( (x;\, y) \) et \( \vec{v} \) a pour coordonnées \( (x’;\, y’) \) dans un repère orthonormé, alors :
Démonstration : Cette formule repose sur la décomposition dans la base orthonormée. En développant \( (x\vec{i} + y\vec{j}) \cdot (x’\vec{i} + y’\vec{j}) \) et en utilisant \( ||\vec{i}|| = ||\vec{j}|| = 1 \) et \( \vec{i} \cdot \vec{j} = 0 \), on obtient directement \( xx’ + yy’ \).
Soit \( \vec{u}(5;\, -4) \) et \( \vec{v}(-3;\, 7) \).
Le résultat négatif indique immédiatement que l’angle entre ces deux vecteurs est obtus.
Propriétés Algébriques et Identités Remarquables du Produit Scalaire
Le produit scalaire hérite de nombreuses propriétés de la multiplication réelle, ce qui permet de manipuler les expressions vectorielles avec aisance.
Symétrie et Bilinéarité
Propriétés : Symétrie et bilinéarité
- Symétrie : \( \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} \) (la démonstration repose sur la parité du cosinus : \( \cos(x) = \cos(-x) \)).
- Distributivité : \( \vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \)
- Compatibilité scalaire : \( \vec{u} \cdot (k\vec{v}) = k(\vec{u} \cdot \vec{v}) \) pour tout réel \( k \).
Carré Scalaire et Norme
Propriété : Carré scalaire
Le produit scalaire d’un vecteur par lui-même est appelé carré scalaire, noté \( \vec{u}^2 \). D’après la définition :
Cette propriété est cruciale car elle permet de transformer des expressions vectorielles en calculs de longueurs.
Les Identités Remarquables Vectorielles
Théorème : Identités remarquables vectorielles
Pour tous vecteurs \( \vec{u} \) et \( \vec{v} \) :
- \( (\vec{u} + \vec{v})^2 = ||\vec{u}||^2 + 2\,\vec{u} \cdot \vec{v} + ||\vec{v}||^2 \)
- \( (\vec{u} – \vec{v})^2 = ||\vec{u}||^2 – 2\,\vec{u} \cdot \vec{v} + ||\vec{v}||^2 \)
- \( (\vec{u} + \vec{v}) \cdot (\vec{u} – \vec{v}) = ||\vec{u}||^2 – ||\vec{v}||^2 \)
Démonstration de la 2ᵉ identité : par double distributivité, \( (\vec{u} – \vec{v}) \cdot (\vec{u} – \vec{v}) = \vec{u}\cdot\vec{u} – \vec{u}\cdot\vec{v} – \vec{v}\cdot\vec{u} + \vec{v}\cdot\vec{v} \), ce qui donne bien le résultat par symétrie.
Formules de Polarisation
Propriété : Formules de polarisation
À partir des identités remarquables, on peut exprimer le produit scalaire uniquement en fonction des normes — très utile si l’on connaît les longueurs des côtés d’un triangle mais pas les angles :
Produit Scalaire, Espace Euclidien et Applications Géométriques
Le produit scalaire est l’outil central de l’espace euclidien. Il permet de généraliser des théorèmes connus comme Pythagore et de résoudre des problèmes métriques complexes.
Orthogonalité des Vecteurs
Théorème : Condition d’orthogonalité
Deux vecteurs \( \vec{u} \) et \( \vec{v} \) sont orthogonaux (perpendiculaires) si et seulement si leur produit scalaire est nul :
Cette équivalence permet de démontrer qu’un triangle est rectangle ou que deux droites sont perpendiculaires simplement en vérifiant une équation algébrique.
Théorème d’Al Kashi (Pythagore Généralisé)
Théorème d’Al Kashi
Le théorème d’Al Kashi permet de calculer le troisième côté d’un triangle quelconque connaissant deux côtés et l’angle inclus. Pour un triangle ABC :
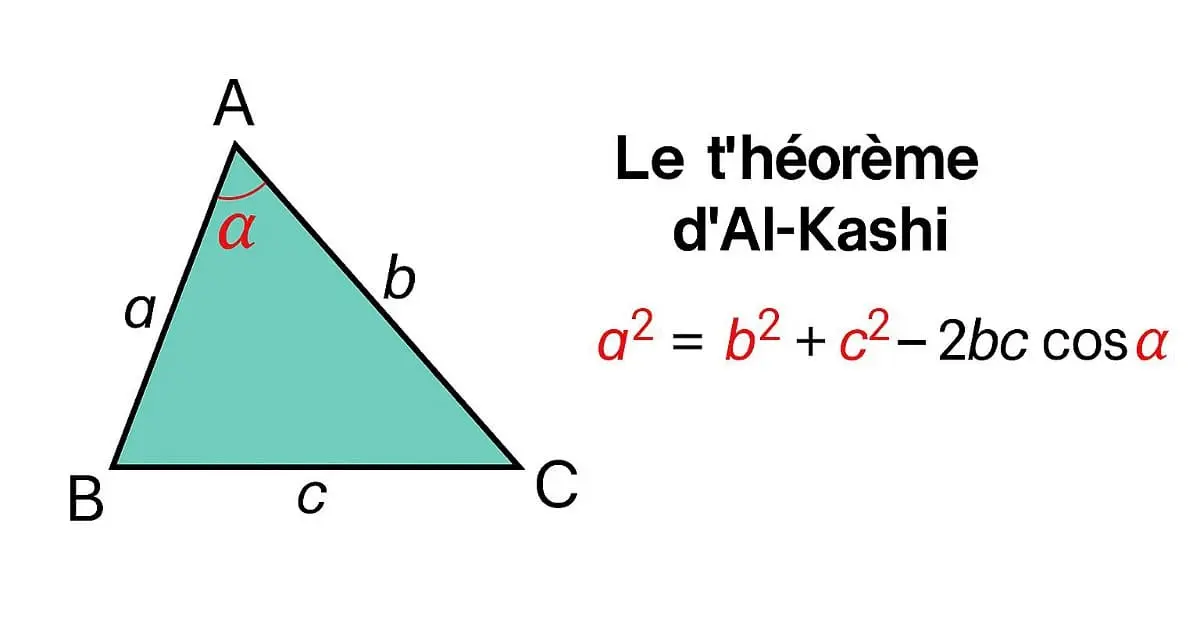
Si le triangle est rectangle en A, l’angle est de 90° et \( \cos(90°) = 0 \) : on retombe sur \( BC^2 = AB^2 + AC^2 \) (théorème de Pythagore). Cette formule est essentielle dans les exercices sur les triangles quelconques.
Théorème de la Médiane
Théorème de la médiane
Soient A et B deux points et I le milieu du segment [AB]. Pour tout point M du plan :
Cette formule est très utilisée pour calculer la longueur d’une médiane sans passer par des coordonnées complexes.
Relations Métriques dans le Triangle Rectangle
Propriété : Relations métriques
Si ABC est un triangle rectangle en A et H le projeté orthogonal de A sur (BC), le produit scalaire permet d’établir :
- \( AH^2 = HB \times HC \)
- \( AB^2 = BH \times BC \)
Ces relations sont des outils puissants pour la géométrie de construction.
Produit Scalaire : Exercices Corrigés et Exemples Détaillés
Pour bien maîtriser ce cours, rien ne vaut la pratique. Voici des exemples concrets tirés de situations classiques.
Exercice 1 : Calcul avec les normes (Formule de polarisation)
Énoncé : Soit un triangle CFG avec \( CF = 7 \), \( FG = 3 \) et \( CG = 6 \). Calculer le produit scalaire \( \vec{CG} \cdot \vec{CF} \).
Solution : Nous ne connaissons pas l’angle, mais nous avons les trois longueurs. Utilisons la formule de polarisation :
Le produit scalaire est 38.
Exercice 2 : Projection orthogonale dans un rectangle
Énoncé : Soit ABCD un rectangle tel que \( AB = 6 \) et \( BC = 4 \). Soit I le milieu de [AB]. Calculer \( \vec{DI} \cdot \vec{DC} \).
Solution : Projetons le point I sur la droite (DC). Appelons H ce projeté orthogonal. Puisque I est le milieu de [AB] et ABCD est un rectangle, H est le milieu de [DC]. On a \( \vec{DC} \) et \( \vec{DH} \) colinéaires et de même sens, donc :
(car \( DH = \frac{1}{2} DC = 3 \) puisque \( AB = DC = 6 \)).
Synthèse : Points Clés à Retenir
Le produit scalaire et ses applications sont vastes. Que ce soit pour vérifier une orthogonalité, calculer une longueur via Al Kashi, ou déterminer un angle, cet outil est incontournable. Il se distingue du produit vectoriel (qui donne un vecteur et s’applique dans l’espace 3D) par sa nature scalaire.
- Le produit scalaire associe un nombre réel à deux vecteurs.
- La formule géométrique utilise l’angle : \(\vec{u} \cdot \vec{v} = ||\vec{u}||\,||\vec{v}||\cos\theta\).
- La formule en coordonnées simplifie les calculs : \(\vec{u} \cdot \vec{v} = xx’ + yy’\).
- Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul.
- Les identités remarquables accélèrent les démonstrations.
- Le théorème d’Al-Kashi étend Pythagore aux triangles quelconques.
- La projection orthogonale offre une interprétation géométrique intuitive.
Questions Fréquentes (FAQ)
Quelle est la différence entre produit scalaire et produit vectoriel ?
La différence fondamentale réside dans le résultat. Le produit scalaire de deux vecteurs donne un nombre réel (scalaire) et est défini dans le plan et l’espace. Le produit vectoriel donne un nouveau vecteur orthogonal aux deux premiers et n’est défini que dans un espace de dimension 3. Le produit scalaire sert à calculer des angles, tandis que le produit vectoriel sert à calculer des aires ou des directions normales.
Comment calculer un produit scalaire sans l’angle ?
Si vous n’avez pas l’angle, deux méthodes sont disponibles : la méthode analytique si vous avez les coordonnées (\( xx’ + yy’ \)), ou la formule de polarisation si vous avez les longueurs des côtés du triangle formé par les vecteurs : \( \frac{1}{2} ( ||\vec{u}||^2 + ||\vec{v}||^2 – ||\vec{u} – \vec{v}||^2 ) \).
Quand le produit scalaire est-il nul ?
Le produit scalaire est nul (\( \vec{u} \cdot \vec{v} = 0 \)) dans deux cas précis : soit l’un des vecteurs est le vecteur nul, soit les deux vecteurs sont orthogonaux (perpendiculaires). C’est le test standard pour prouver la perpendicularité en géométrie.
Où trouver un résumé du cours produit scalaire en PDF ?
Bien que cette page web serve de référence complète, de nombreuses ressources académiques proposent le cours en PDF. Cependant, ce guide en ligne est régulièrement mis à jour et intègre directement les démonstrations et exemples interactifs nécessaires à votre compréhension.