Les fonctions mathématiques constituent un pilier fondamental de l’analyse moderne. Comprendre les généralités sur les fonctions permet de modéliser des phénomènes réels complexes, de la trajectoire d’un projectile aux variations économiques. Ce cours présente de manière structurée les définitions essentielles, les propriétés des fonctions et leurs représentations graphiques, avec des exemples concrets pour faciliter l’apprentissage.
Définitions Fondamentales et Domaine de Définition
Définition d’une Fonction
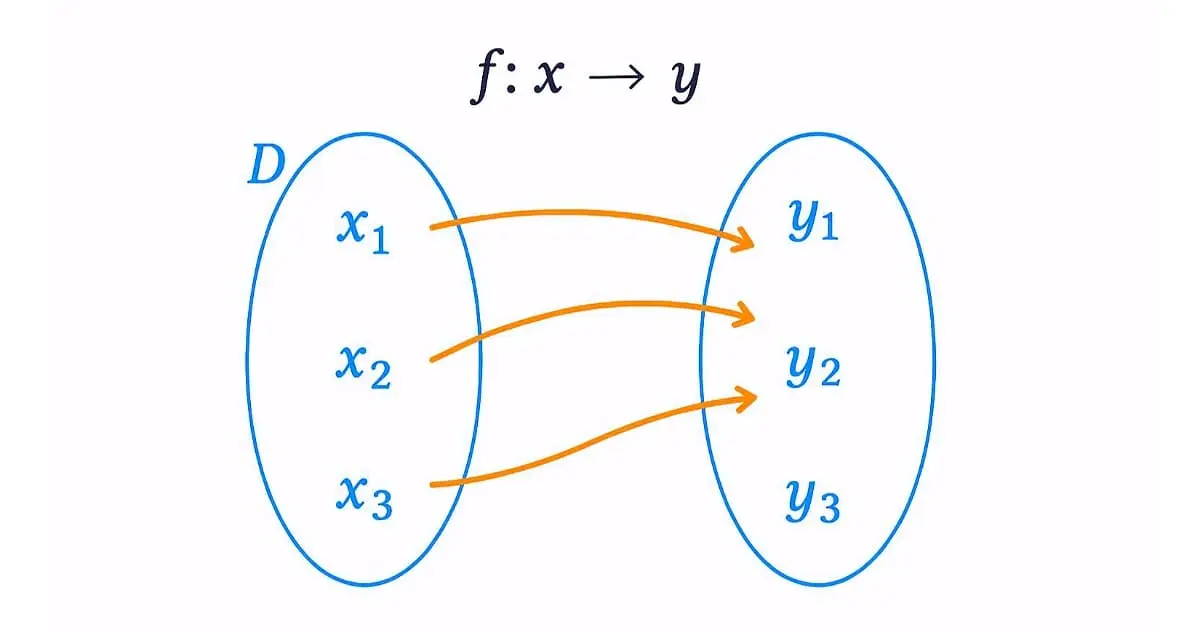
Une fonction est une relation mathématique qui associe à chaque nombre x appartenant à un ensemble D un unique nombre y. On note cette correspondance par \( f : x \mapsto y \) ou encore \( y = f(x) \).
Dans cette notation, y représente l’image de x par la fonction f, tandis que x est appelé antécédent de y par la fonction f.
Domaine de Définition
Le domaine de définition d’une fonction f, noté \( D_f \), désigne l’ensemble de tous les nombres réels qui possèdent une image par cette fonction. Autrement dit, \( D_f \) regroupe toutes les valeurs de x pour lesquelles \( f(x) \) existe et est définie.
Égalité de Fonctions et Représentation Graphique
Égalité de Deux Fonctions
Soient f et g deux fonctions de domaines respectifs \( D_f \) et \( D_g \). On dit que f et g sont égales, noté \( f = g \), si et seulement si deux conditions sont simultanément remplies.
Premièrement, les domaines de définition doivent être identiques : \( D_f = D_g \). Deuxièmement, pour tout élément \( x \in D_f \) (ou \( x \in D_g \)), on doit avoir \( f(x) = g(x) \).
Représentation Graphique
Soit f une fonction de domaine \( D_f \). La courbe représentative de la fonction f, notée \( \mathcal{C}_f \), est constituée de l’ensemble des points \( M(x, f(x)) \) où x parcourt le domaine de définition.
Fonctions Paires et Fonctions Impaires
Fonction Paire
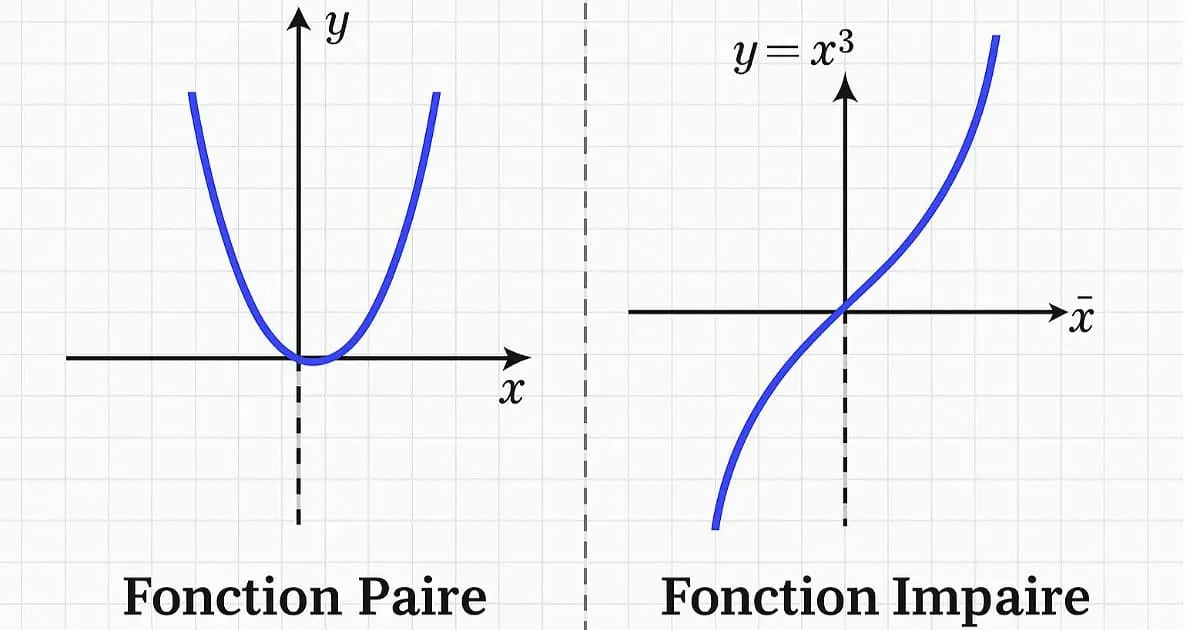
Une fonction f est qualifiée de fonction paire lorsque deux conditions essentielles sont vérifiées. D’abord, le domaine de définition doit être symétrique par rapport à zéro, c’est-à-dire que si \( x \in D_f \), alors \( -x \in D_f \). Ensuite, pour tout réel x du domaine, on doit avoir l’égalité suivante.
La courbe représentative d’une fonction paire présente une symétrie axiale par rapport à l’axe des ordonnées. Cette propriété graphique permet d’identifier visuellement la parité d’une fonction.
Fonction Impaire
Une fonction f est dite fonction impaire si son domaine de définition est symétrique par rapport à zéro et si pour tout réel x appartenant à \( D_f \), la relation suivante est satisfaite.
Graphiquement, la courbe d’une fonction impaire possède une symétrie centrale par rapport à l’origine du repère. Cette caractéristique facilite grandement l’étude de la fonction sur l’ensemble de son domaine.
Variations d’une Fonction Numérique
Fonction Strictement Croissante
Soit f une fonction définie sur un intervalle I inclus dans \( D_f \). On dit que f est strictement croissante sur I lorsque l’ordre entre deux éléments est conservé par la fonction.
Formellement, pour tous \( x_1, x_2 \in I \) tels que \( x_1 < x_2 \), on a nécessairement \( f(x_1) < f(x_2) \). Une fonction croissante conserve donc l’ordre initial des valeurs.
Fonction Strictement Décroissante
Une fonction f est strictement décroissante sur un intervalle I si elle inverse l’ordre des éléments. Ainsi, pour tous \( x_1, x_2 \in I \) vérifiant \( x_1 < x_2 \), on obtient \( f(x_1) > f(x_2) \).
Fonction Constante
Une fonction f est constante sur un intervalle I s’il existe un réel k tel que pour tout \( x \in I \), on ait \( f(x) = k \). Les images de tous les éléments de l’intervalle sont donc identiques.
Taux d’Accroissement
Le taux d’accroissement permet de caractériser algébriquement les variations d’une fonction. Pour une fonction f définie sur un intervalle I et pour deux points distincts \( x_1, x_2 \in I \) avec \( x_1 \neq x_2 \), le taux d’accroissement s’écrit sous la forme suivante.
Une fonction est strictement croissante sur I si et seulement si ce taux est strictement positif pour tous \( x_1, x_2 \in I \) avec \( x_1 \neq x_2 \). Elle est strictement décroissante si ce taux est strictement négatif.
Variations et Parité
Soit f une fonction numérique définie sur un intervalle I et soit I’ l’intervalle symétrique de I par rapport à zéro. Les propriétés de parité influencent directement les variations.
Si f est paire, alors elle est croissante sur I si et seulement si elle est décroissante sur I’. À l’inverse, si f est impaire, elle conserve son sens de variation : croissante sur I équivaut à croissante sur I’.
Extremums d’une Fonction
Maximum Local
Soit f une fonction définie sur un intervalle ouvert I et soit \( a \in I \). On dit que \( f(a) \) est une valeur maximale de f sur I (ou un maximum de f sur I) si pour tout \( x \in I \), on a l’inégalité suivante.
Minimum Local
De manière similaire, \( f(a) \) est une valeur minimale de f sur I (ou un minimum de f sur I) si pour tout élément \( x \in I \), on vérifie que \( f(x) \geq f(a) \).
Étude des Fonctions Polynômes du Second Degré
Fonction Carrée : \( f(x) = ax^2 \)
Considérons une fonction de la forme \( f(x) = ax^2 \) où \( a \in \mathbb{R}^* \). Cette fonction est une fonction paire car son domaine est \( \mathbb{R} \) et elle vérifie \( f(-x) = f(x) \).
Pour \( a > 0 \), la fonction est strictement décroissante sur \( ]-\infty, 0] \) et strictement croissante sur \( [0, +\infty[ \). Elle admet un minimum en zéro valant \( f(0) = 0 \).
Pour \( a < 0 \), le sens de variation s’inverse et la fonction admet un maximum en zéro. La courbe représentative est une parabole de sommet l’origine du repère et d’axe de symétrie l’axe des ordonnées.
Fonction Trinôme : \( f(x) = ax^2 + bx + c \)
Soit f une fonction définie par \( f(x) = ax^2 + bx + c \) avec \( a \neq 0 \). Le domaine de définition est \( D_f = \mathbb{R} \) car il s’agit d’une fonction polynôme.
On peut réécrire cette expression sous forme canonique en complétant le carré. On obtient ainsi la formulation suivante.
Les paramètres sont définis par \( \alpha = -\frac{b}{2a} \) et \( \beta = f(\alpha) = \frac{-\Delta}{4a} \) où \( \Delta = b^2 – 4ac \) représente le discriminant.
La courbe représentative \( \mathcal{C}_f \) est une parabole de sommet \( S(\alpha, \beta) \) et d’axe de symétrie la droite verticale d’équation \( x = \alpha \). Les variations dépendent du signe de a : si \( a > 0 \), la fonction décroît sur \( ]-\infty, \alpha] \) puis croît sur \( [\alpha, +\infty[ \) avec un minimum en \( \alpha \).
Étude des Fonctions Homographiques
Fonction Inverse : \( f(x) = \frac{a}{x} \)
Considérons la fonction définie par \( f(x) = \frac{a}{x} \) où \( a \in \mathbb{R}^* \). Le domaine de définition est \( D_f = \mathbb{R}^* = \mathbb{R} \setminus \{0\} \) car la division par zéro est interdite.
Cette fonction est impaire puisque \( f(-x) = \frac{a}{-x} = -\frac{a}{x} = -f(x) \). Pour \( a > 0 \), elle est strictement décroissante sur chacun des intervalles \( ]-\infty, 0[ \) et \( ]0, +\infty[ \).
La courbe représentative est une hyperbole de centre l’origine du repère. Elle admet deux asymptotes : l’axe des abscisses (asymptote horizontale d’équation \( y = 0 \)) et l’axe des ordonnées (asymptote verticale d’équation \( x = 0 \)).
Fonction Homographique Générale
Une fonction de la forme \( f(x) = \frac{ax + b}{cx + d} \) avec \( a, c \neq 0 \) et \( ad – bc \neq 0 \) est appelée fonction homographique. Elle se définit pour tout \( x \neq -\frac{d}{c} \).
En effectuant la division euclidienne du numérateur par le dénominateur, on obtient la forme réduite suivante.
La courbe \( \mathcal{C}_f \) est une hyperbole de centre \( W(\alpha, \beta) \) et d’asymptotes les droites d’équations \( x = \alpha \) (verticale) et \( y = \beta \) (horizontale).
Si \( \lambda > 0 \), la fonction est décroissante sur chacun des intervalles \( ]-\infty, \alpha[ \) et \( ]\alpha, +\infty[ \). Si \( \lambda < 0 \), elle est croissante sur ces mêmes intervalles.
Position Relative de Courbes et Résolution Graphique
Intersection de Deux Courbes
Soient \( \mathcal{C}_f \) et \( \mathcal{C}_g \) les courbes représentatives respectives de deux fonctions f et g. Un point \( M(x, y) \) appartient simultanément aux deux courbes si et seulement si \( y = f(x) \) et \( y = g(x) \).
Par conséquent, les abscisses des points d’intersection de \( \mathcal{C}_f \) et \( \mathcal{C}_g \) sont les solutions de l’équation algébrique suivante.
Position Relative
Pour déterminer quelle courbe se situe au-dessus de l’autre sur un intervalle donné, on étudie le signe de la différence \( f(x) – g(x) \).
Les solutions de l’inéquation \( f(x) > g(x) \) correspondent aux abscisses des points de \( \mathcal{C}_f \) situés au-dessus de \( \mathcal{C}_g \). Inversement, les solutions de \( f(x) < g(x) \) donnent les abscisses où \( \mathcal{C}_f \) se trouve en-dessous de \( \mathcal{C}_g \).
Équation et Inéquation avec une Droite Horizontale
Considérons l’équation \( f(x) = m \) où m est un réel fixé. Les solutions représentent les abscisses des points d’intersection entre la courbe \( \mathcal{C}_f \) et la droite horizontale d’équation \( y = m \).
De même, résoudre l’inéquation \( f(x) > m \) revient à identifier les intervalles sur lesquels la courbe \( \mathcal{C}_f \) se situe strictement au-dessus de cette droite horizontale.
Résumé des Concepts Clés
Les généralités sur les fonctions constituent un socle indispensable pour toute étude mathématique approfondie. Une fonction associe à chaque élément d’un domaine de définition une unique image. La parité d’une fonction (paire ou impaire) détermine des symétries graphiques spécifiques et simplifie l’étude des variations.
Les variations d’une fonction se caractérisent par le signe de son taux d’accroissement. Une fonction strictement croissante conserve l’ordre tandis qu’une fonction strictement décroissante l’inverse. Les extremums locaux correspondent aux points où la fonction atteint ses valeurs maximales ou minimales sur un intervalle donné.
Les fonctions polynômes du second degré produisent des paraboles dont la forme canonique révèle immédiatement le sommet et l’axe de symétrie. Les fonctions homographiques génèrent des hyperboles caractérisées par leur centre et leurs asymptotes verticale et horizontale.
Enfin, l’étude de la position relative de courbes permet de résoudre graphiquement des équations et inéquations en identifiant les zones où une courbe domine l’autre. Ces techniques graphiques complètent harmonieusement les méthodes algébriques classiques.
Questions Fréquentes sur les Généralités des Fonctions
Comment déterminer le domaine de définition d’une fonction ?
Pour déterminer le domaine de définition, il faut identifier les valeurs de x qui rendent l’expression de la fonction impossible à calculer. Les cas principaux à vérifier sont les divisions par zéro (le dénominateur ne doit jamais s’annuler), les racines carrées de nombres négatifs (l’expression sous le radical doit être positive ou nulle), et les logarithmes d’arguments non positifs. Par exemple, pour la fonction \( f(x) = \frac{1}{x-2} \), le domaine est \( D_f = \mathbb{R} \setminus \{2\} \) car x ne peut pas valoir 2.
Quelle est la différence entre une fonction paire et une fonction impaire ?
Une fonction paire vérifie la relation \( f(-x) = f(x) \) pour tout x de son domaine, ce qui se traduit graphiquement par une symétrie axiale par rapport à l’axe des ordonnées. Un exemple classique est la fonction carrée \( f(x) = x^2 \). Une fonction impaire satisfait \( f(-x) = -f(x) \), produisant une symétrie centrale par rapport à l’origine du repère. La fonction cube \( f(x) = x^3 \) illustre parfaitement ce cas. Ces propriétés permettent de réduire de moitié l’étude de la fonction.
Comment savoir si une fonction est croissante ou décroissante ?
Une méthode efficace consiste à calculer le taux d’accroissement entre deux points distincts de l’intervalle étudié. Si ce quotient est toujours positif, la fonction est croissante car elle conserve l’ordre des valeurs. S’il est toujours négatif, la fonction est décroissante car elle inverse l’ordre. Graphiquement, une fonction croissante monte de gauche à droite tandis qu’une fonction décroissante descend. Pour les fonctions dérivables, l’étude du signe de la dérivée constitue une méthode encore plus puissante.
Qu’est-ce qu’une forme canonique et pourquoi est-elle utile ?
La forme canonique d’un trinôme du second degré s’écrit \( f(x) = a(x – \alpha)^2 + \beta \) où le point \( S(\alpha, \beta) \) représente le sommet de la parabole. Cette écriture est particulièrement utile car elle révèle directement les coordonnées du sommet sans calcul supplémentaire, l’axe de symétrie d’équation \( x = \alpha \), et le sens de variation de la fonction. Elle facilite également le tracé précis de la courbe et la résolution d’équations et inéquations.
Comment identifier les asymptotes d’une fonction homographique ?
Pour une fonction homographique \( f(x) = \frac{ax+b}{cx+d} \), l’asymptote verticale correspond à la valeur interdite qui annule le dénominateur, soit \( x = -\frac{d}{c} \). L’asymptote horizontale s’obtient en calculant la limite de la fonction quand x tend vers l’infini, ce qui donne \( y = \frac{a}{c} \). Ces deux droites se croisent au centre de l’hyperbole, point de référence essentiel pour le tracé de la courbe. La forme réduite permet de visualiser immédiatement ces asymptotes.
Quelle est l’utilité de comparer graphiquement deux fonctions ?
La comparaison graphique de deux fonctions permet de résoudre visuellement des équations et inéquations qui seraient parfois complexes par calcul algébrique. En identifiant les points d’intersection, on obtient les solutions de l’équation \( f(x) = g(x) \). En déterminant les zones où une courbe domine l’autre, on résout les inéquations correspondantes. Cette approche intuitive complète les méthodes analytiques et offre une compréhension géométrique profonde des relations entre fonctions.
En pratique, maîtriser les généralités sur les fonctions nécessite un entraînement régulier à travers la résolution d’exercices variés. Comme le dit le proverbe : « C’est en forgeant que l’on devient forgeron ». La pratique systématique des calculs et des représentations graphiques transforme progressivement ces concepts abstraits en outils naturels de raisonnement mathématique.