Dès les premières semaines de classe préparatoire ou de licence de mathématiques,
le concept d’espace vectoriel s’impose comme la pierre angulaire de
toute l’algèbre linéaire. Pourtant, sa définition abstraite déroute souvent les
étudiants : pourquoi parler de « vecteurs » quand on manipule aussi bien des
polynômes, des matrices ou des fonctions continues ? Ce cours répond précisément
à cette question, en construisant pas à pas la notion d’espace vectoriel,
en illustrant chaque idée par des exemples concrets pour ancrer votre compréhension.
Définition formelle d’un espace vectoriel
Informellement, un espace vectoriel est un ensemble dont les
éléments (appelés vecteurs) peuvent être additionnés entre eux et
multipliés par des nombres (appelés scalaires), de façon que ces deux
opérations se comportent « raisonnablement ». La définition formelle précise exactement
ce que « raisonnablement » veut dire, au travers de huit axiomes.
Définition : K-espace vectoriel
Soit \( \mathbb{K} \) un corps (en pratique \( \mathbb{R} \) ou \( \mathbb{C} \)).
Un \(\mathbb{K}\)-espace vectoriel est un ensemble non vide \( E \)
muni de deux lois :
-
une loi de composition interne \( + : E \times E \to E \),
appelée addition vectorielle ; -
une loi de composition externe
\( \cdot : \mathbb{K} \times E \to E \),
appelée multiplication par un scalaire,
vérifiant les huit axiomes suivants, pour tous
\( u, v, w \in E \) et tous \( \lambda, \mu \in \mathbb{K} \) :
- \( (u + v) + w = u + (v + w) \) : associativité de \(+\)
- \( u + v = v + u \) : commutativité de \(+\)
- Il existe \( \mathbf{0}_E \in E \) tel que \( u + \mathbf{0}_E = u \) : vecteur nul
- Il existe \( -u \in E \) tel que \( u + (-u) = \mathbf{0}_E \) : opposé
- \( 1 \cdot u = u \) : élément neutre scalaire
- \( (\lambda\mu) \cdot u = \lambda \cdot (\mu \cdot u) \) : associativité mixte
- \( \lambda \cdot (u + v) = \lambda \cdot u + \lambda \cdot v \) : distributivité (côté vecteur)
- \( (\lambda + \mu) \cdot u = \lambda \cdot u + \mu \cdot u \) : distributivité (côté scalaire)
Les éléments de \( E \) sont appelés vecteurs et les éléments
de \( \mathbb{K} \) sont appelés scalaires.
Les quatre premiers axiomes signifient exactement que \( (E, +) \) est un
groupe abélien. Les quatre suivants règlent les interactions entre
scalaires et vecteurs.
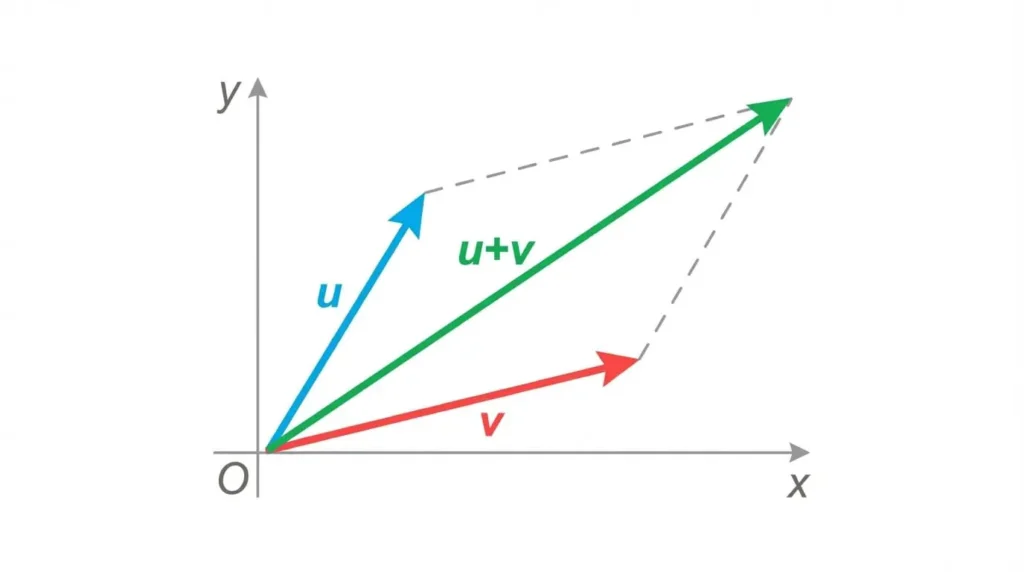
Intuition géométrique : pourquoi cette structure ?
L’idée clé est l’unification. Des objets mathématiques très
différents partagent les mêmes propriétés de base :
-
Les flèches du plan \( \mathbb{R}^2 \) : on peut les additionner
(règle du parallélogramme) et les allonger ou rétrécir (multiplication par un réel). -
Les polynômes \( \mathbb{R}[X] \) : on peut en additionner deux
et multiplier un polynôme par un réel. -
Les fonctions continues \( \mathcal{C}([a,b], \mathbb{R}) \) :
la somme de deux fonctions continues est continue ; le produit d’une fonction
continue par un réel l’est aussi. -
Les matrices \( \mathcal{M}_{n,p}(\mathbb{R}) \) : addition
terme à terme et multiplication par un scalaire.
En abstrayant ces situations, on obtient un cadre unique — l’espace vectoriel —
dans lequel un seul théorème vaut pour tous ces exemples à la fois. C’est toute
la puissance de l’algèbre linéaire.
Exemples fondamentaux d’espaces vectoriels
L’espace \( \mathbb{R}^n \)
C’est l’exemple de référence. Pour \( n \geq 1 \), on pose
\( E = \mathbb{R}^n \) et \( \mathbb{K} = \mathbb{R} \). Un vecteur est un
\( n \)-uplet \( (x_1, \ldots, x_n) \). Les lois sont :
(x_1,\ldots,x_n) + (y_1,\ldots,y_n) = (x_1+y_1,\ldots,x_n+y_n),
\quad
\lambda \cdot (x_1,\ldots,x_n) = (\lambda x_1,\ldots,\lambda x_n).
\]
Le vecteur nul est \( \mathbf{0} = (0,\ldots,0) \).
La vérification des huit axiomes est immédiate d’après les propriétés de
\( \mathbb{R} \).
L’espace des polynômes \( \mathbb{K}[X] \)
L’ensemble de tous les polynômes à coefficients dans \( \mathbb{K} \), muni de
l’addition usuelle et de la multiplication par un scalaire, est un
\( \mathbb{K} \)-espace vectoriel. Le vecteur nul est le polynôme nul \( 0 \).
Notez que cet espace est de dimension infinie, car la famille
\( (1, X, X^2, X^3, \ldots) \) est infinie et forme une base.
L’espace des matrices \( \mathcal{M}_{n,p}(\mathbb{K}) \)
Les matrices \( n \times p \) à coefficients dans \( \mathbb{K} \), munies de
l’addition terme à terme et de la multiplication par un scalaire, forment un
\( \mathbb{K} \)-espace vectoriel de dimension \( np \).
L’espace des fonctions \( \mathcal{F}(A, \mathbb{K}) \)
Pour tout ensemble \( A \), l’ensemble de toutes les fonctions de \( A \) dans
\( \mathbb{K} \), muni de l’addition \( (f+g)(x) = f(x)+g(x) \) et de la
multiplication \( (\lambda f)(x) = \lambda f(x) \), est un
\( \mathbb{K} \)-espace vectoriel. En particulier, \( \mathcal{C}([a,b],\mathbb{R}) \)
est un \( \mathbb{R} \)-espace vectoriel.
| Espace \( E \) | Corps \( \mathbb{K} \) | Vecteur nul | Dimension |
|---|---|---|---|
| \( \mathbb{R}^n \) | \( \mathbb{R} \) | \( (0,\ldots,0) \) | \( n \) |
| \( \mathcal{M}_{n,p}(\mathbb{R}) \) | \( \mathbb{R} \) | Matrice nulle | \( np \) |
| \( \mathbb{R}_n[X] \) (degrés \( \leq n \)) | \( \mathbb{R} \) | Polynôme nul | \( n+1 \) |
| \( \mathbb{R}[X] \) | \( \mathbb{R} \) | Polynôme nul | \( +\infty \) |
| \( \mathcal{C}([a,b],\mathbb{R}) \) | \( \mathbb{R} \) | Fonction nulle | \( +\infty \) |
Propriétés immédiates déduites des axiomes
Proposition : Conséquences des axiomes
Soit \( E \) un \( \mathbb{K} \)-espace vectoriel. Pour tout \( u \in E \) et
tout \( \lambda \in \mathbb{K} \) :
- \( 0_\mathbb{K} \cdot u = \mathbf{0}_E \) (le scalaire zéro annule tout vecteur)
- \( \lambda \cdot \mathbf{0}_E = \mathbf{0}_E \) (tout scalaire annule le vecteur nul)
- \( (-1) \cdot u = -u \) (l’opposé est obtenu par multiplication par \(-1\))
- \( \lambda \cdot u = \mathbf{0}_E \implies \lambda = 0_\mathbb{K} \text{ ou } u = \mathbf{0}_E \)
Démonstration de \( 0_\mathbb{K} \cdot u = \mathbf{0}_E \)
On part de la relation \( 0_\mathbb{K} + 0_\mathbb{K} = 0_\mathbb{K} \) dans
\( \mathbb{K} \). En multipliant par \( u \) (axiome 8) :
(0_\mathbb{K} + 0_\mathbb{K}) \cdot u = 0_\mathbb{K} \cdot u
\implies
0_\mathbb{K} \cdot u + 0_\mathbb{K} \cdot u = 0_\mathbb{K} \cdot u.
\]
En ajoutant \( -(0_\mathbb{K} \cdot u) \) des deux côtés, on obtient
\( 0_\mathbb{K} \cdot u = \mathbf{0}_E \). \( \square \)
Sous-espace vectoriel : définition et caractérisation
Dans la pratique, on ne repart pas de zéro pour vérifier les huit axiomes :
on part d’un espace vectoriel déjà connu et on identifie des parties qui en
héritent la structure. C’est le concept de sous-espace vectoriel.
Définition : Sous-espace vectoriel (s.e.v.)
Soit \( E \) un \( \mathbb{K} \)-espace vectoriel et \( F \subseteq E \).
On dit que \( F \) est un sous-espace vectoriel de \( E \) si
et seulement si les trois conditions suivantes sont satisfaites :
- \( \mathbf{0}_E \in F \) (F contient le vecteur nul)
- Pour tous \( u, v \in F \), on a \( u + v \in F \) (stabilité par addition)
- Pour tout \( u \in F \) et tout \( \lambda \in \mathbb{K} \), on a \( \lambda u \in F \) (stabilité par multiplication scalaire)
Ces trois conditions se condensent souvent en une seule : \( F \) est un
s.e.v. de \( E \) si et seulement si \( F \neq \emptyset \) et pour tous
\( u, v \in F \) et \( \lambda, \mu \in \mathbb{K} \) :
\lambda u + \mu v \in F.
\]
Exemples de sous-espaces vectoriels
Exemple 1. Dans \( \mathbb{R}^2 \), la droite vectorielle
\( F = \{(x, y) \in \mathbb{R}^2 \mid y = 2x\} \) est un s.e.v. :
\( (0,0) \in F \) ; si \( (x_1, 2x_1) \) et \( (x_2, 2x_2) \) sont dans \( F \),
leur somme \( (x_1+x_2, 2(x_1+x_2)) \in F \) ; et \( \lambda(x, 2x) = (\lambda x, 2\lambda x) \in F \).
Exemple 2. Dans \( \mathbb{R}^2 \), l’ensemble
\( G = \{(x, y) \mid x + y = 1\} \) n’est pas un s.e.v. car
\( \mathbf{0} = (0,0) \notin G \).
Exemple 3. Dans \( \mathbb{R}[X] \), l’ensemble
\( \mathbb{R}_n[X] \) des polynômes de degré inférieur ou égal à \( n \) est un
s.e.v. En revanche, l’ensemble des polynômes de degré exactement \( n \)
ne l’est pas (la somme de deux polynômes de degré \( n \) peut avoir un degré
strictement inférieur à \( n \)).
Combinaison linéaire et sous-espace engendré
Définition : Combinaison linéaire
Soient \( v_1, \ldots, v_n \) des vecteurs d’un \( \mathbb{K} \)-espace
vectoriel \( E \). Tout vecteur de la forme
u = \lambda_1 v_1 + \lambda_2 v_2 + \cdots + \lambda_n v_n,
\quad \lambda_1,\ldots,\lambda_n \in \mathbb{K},
\]
est appelé combinaison linéaire des vecteurs
\( v_1, \ldots, v_n \). Les scalaires \( \lambda_i \) sont les
coefficients de la combinaison.
Définition : Sous-espace engendré
L’ensemble de toutes les combinaisons linéaires d’une famille
\( (v_1, \ldots, v_n) \) est noté
\( \operatorname{Vect}(v_1, \ldots, v_n) \) et s’appelle le
sous-espace vectoriel engendré par cette famille. C’est le
plus petit sous-espace vectoriel de \( E \) contenant tous les \( v_i \).
\operatorname{Vect}(v_1,\ldots,v_n)
= \left\{ \sum_{i=1}^{n} \lambda_i v_i \;\middle|\; \lambda_i \in \mathbb{K} \right\}.
\]
Famille libre, famille génératrice et base d’un espace vectoriel
Ces trois notions sont indissociables et au cœur de toute la théorie.
Définition : Famille libre (ou linéairement indépendante)
Une famille \( (v_1,\ldots,v_n) \) est dite libre si
\lambda_1 v_1 + \cdots + \lambda_n v_n = \mathbf{0}_E
\implies
\lambda_1 = \cdots = \lambda_n = 0.
\]
Autrement dit, la seule façon d’obtenir le vecteur nul comme combinaison
linéaire est la combinaison triviale (tous les coefficients nuls).
Définition : Famille génératrice
Une famille \( (v_1,\ldots,v_n) \) est génératrice de \( E \)
si tout vecteur de \( E \) s’écrit comme combinaison linéaire des \( v_i \),
c’est-à-dire si \( \operatorname{Vect}(v_1,\ldots,v_n) = E \).
Définition-Théorème : Base d’un espace vectoriel
Une famille \( \mathcal{B} = (e_1,\ldots,e_n) \) est une
base de \( E \) si elle est à la fois
libre et génératrice. Dans ce cas, tout vecteur
\( u \in E \) se décompose de façon unique :
u = x_1 e_1 + \cdots + x_n e_n, \quad x_i \in \mathbb{K}.
\]
Les scalaires \( (x_1,\ldots,x_n) \) sont appelés les
coordonnées (ou composantes) de \( u \) dans la base
\( \mathcal{B} \).
Base canonique de \( \mathbb{R}^n \)
La famille \( \mathcal{B}_c = (e_1,\ldots,e_n) \) où
\( e_i = (0,\ldots,0,1,0,\ldots,0) \) (le 1 en position \( i \)) est la
base canonique de \( \mathbb{R}^n \). Tout vecteur
\( (x_1,\ldots,x_n) \) s’écrit \( x_1 e_1 + \cdots + x_n e_n \).
Dimension d’un espace vectoriel
Théorème : Invariance de la dimension
Si un espace vectoriel \( E \) admet une base finie de \( n \) éléments,
alors toutes ses bases ont exactement \( n \) éléments. Ce nombre
\( n \) est appelé la dimension de \( E \) et noté
\( \dim(E) \) ou \( \dim_\mathbb{K}(E) \).
Ce théorème, non trivial, est l’une des raisons pour lesquelles la notion de
dimension est bien définie. En particulier :
- \( \dim(\mathbb{R}^n) = n \)
- \( \dim(\mathcal{M}_{n,p}(\mathbb{R})) = np \)
- \( \dim(\mathbb{R}_n[X]) = n+1 \)
- \( \dim(\mathbb{R}[X]) = +\infty \)
- Par convention, \( \dim(\{\mathbf{0}\}) = 0 \)
Propriété Dimension et sous-espaces
Soit \( F \) un sous-espace vectoriel d’un espace vectoriel de dimension
finie \( E \). Alors :
- \( \dim(F) \leq \dim(E) \)
- \( \dim(F) = \dim(E) \implies F = E \)
- La formule de Grassmann : \( \dim(F+G) = \dim F + \dim G – \dim(F \cap G) \)
Conclusion
L’espace vectoriel est bien plus qu’une simple généralisation
des vecteurs du plan ou de l’espace : c’est un cadre abstrait et puissant qui
unifie des situations mathématiques très variées (géométrie, analyse, algèbre).
Maîtriser la définition formelle avec ses huit axiomes, savoir reconnaître un
sous-espace vectoriel, comprendre les notions de
combinaison linéaire, de famille libre, de
famille génératrice et de base, et savoir calculer la
dimension d’un espace vectoriel — voilà les compétences fondamentales
de l’algèbre linéaire.
Les exercices corrigés montrent que la méthode est toujours la même :
vérifier point par point les conditions de la définition, sans jamais
sauter d’étape. Avec de la pratique, ces vérifications deviennent rapides et
naturelles.