Le calcul du déterminant d’une matrice est l’une des compétences fondamentales de l’algèbre linéaire. Que vous soyez en Terminale spécialité mathématiques, en MPSI, en L1 ou en L2, maîtriser le déterminant d’une matrice vous permettra de résoudre des systèmes linéaires, de tester l’inversibilité d’une matrice et d’interpréter géométriquement des transformations. Cette page couvre toutes les méthodes, de la plus élémentaire à la plus générale — calculs de déterminants 2×2, 3×3 et n×n avec des preuves rigoureuses.
Qu’est-ce qu’un déterminant ? Définition et premières propriétés
Intuitivement, le calcul du déterminant d’une matrice carrée produit un nombre qui encode des informations essentielles sur la matrice : est-elle inversible ? quelle aire ou quel volume représentent ses vecteurs colonnes ? Le déterminant agit comme un « résumé algébrique » de la transformation linéaire associée à la matrice.
Définition : Déterminant d’une matrice carrée
Soit \( A = (a_{i,j})_{1 \le i,j \le n} \) une matrice carrée de taille \( n \times n \) à coefficients dans un corps \( \mathbb{K} \) (par exemple \( \mathbb{R} \) ou \( \mathbb{C} \)). Le déterminant de \( A \), noté \( \det(A) \) ou \( |A| \), est l’unique scalaire défini par la formule de Leibniz :
\det(A) = \sum_{\sigma \in \mathfrak{S}_n} \varepsilon(\sigma) \prod_{i=1}^{n} a_{i,\sigma(i)}
\]
où \( \mathfrak{S}_n \) désigne l’ensemble des permutations de \( \{1, \ldots, n\} \) et \( \varepsilon(\sigma) \in \{+1, -1\} \) est la signature de la permutation \( \sigma \).
Cette formule est remarquable sur le plan théorique, mais elle n’est pratiquement pas utilisable dès que \( n \ge 4 \) : elle nécessiterait en effet \( n! \) produits (pour \( n = 4 \), c’est déjà 24 termes). C’est précisément pourquoi il existe des méthodes de calcul bien plus efficaces, que nous allons détailler une à une.
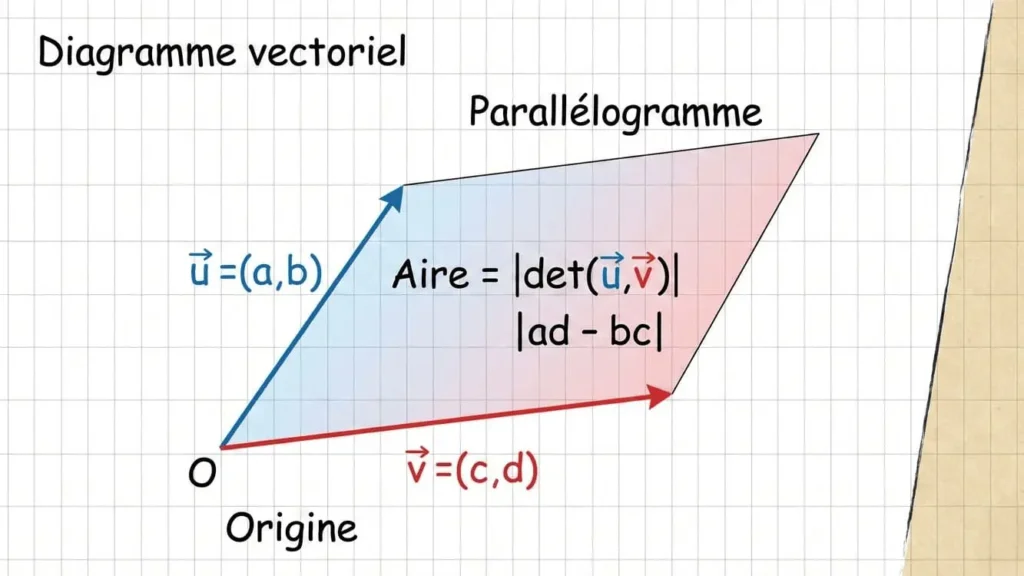
Interprétation géométrique : aire et volume orientés
Avant même de calculer quoi que ce soit, il faut voir ce que représente le déterminant. En dimension 2, si l’on place deux vecteurs \( \vec{u} = (a, b) \) et \( \vec{v} = (c, d) \) dans le plan, le déterminant de la matrice qu’ils forment est exactement l’aire algébrique du parallélogramme qu’ils engendrent :
\det\begin{pmatrix} a & c \\ b & d \end{pmatrix} = ad – bc = \text{aire algébrique du parallélogramme } (\vec{u}, \vec{v})
\]
En dimension 3, le déterminant donne le volume algébrique du parallélépipède engendré par trois vecteurs. Le signe du déterminant indique l’orientation : positif si les vecteurs forment une base directe (comme la base canonique), négatif sinon. C’est là l’essence géométrique du déterminant, bien au-delà de la simple formule de calcul.
Propriétés fondamentales du déterminant
Toutes les méthodes efficaces de calcul du déterminant reposent sur ces propriétés. Les comprendre, c’est pouvoir les utiliser comme outils, pas comme règles à mémoriser aveuglément.
Propriété 1 : Multilinéarité alternée
Le déterminant est linéaire par rapport à chaque ligne (et chaque colonne) séparément. Cela signifie notamment :
- Si l’on multiplie une ligne par un scalaire \( \lambda \), le déterminant est multiplié par \( \lambda \).
- Si deux lignes (ou colonnes) sont égales, le déterminant est nul.
- Si l’on échange deux lignes, le déterminant change de signe.
Propriété 2 : Opérations élémentaires sur les lignes et les colonnes
Ces trois opérations régissent la méthode du pivot de Gauss :
- Ajouter à une ligne un multiple d’une autre ligne : ne change pas le déterminant.
- Multiplier une ligne par \( \lambda \neq 0 \) : multiplie le déterminant par \( \lambda \).
- Échanger deux lignes : change le signe du déterminant.
Ces mêmes règles s’appliquent exactement de la même façon aux colonnes.
Théorème : Invariance par transposition et multiplicativité
Soient \( A \) et \( B \) deux matrices carrées de même taille \( n \). Alors :
\det(A^\top) = \det(A)
\qquad \text{et} \qquad
\det(AB) = \det(A) \cdot \det(B)
\]
La première relation est cruciale : elle signifie que tout ce qu’on peut faire sur les lignes, on peut le faire sur les colonnes. La seconde (formule du produit) permet de calculer le déterminant d’un produit sans calculer le produit lui-même.
Théorème : Critère d’inversibilité
Une matrice carrée \( A \) est inversible si et seulement si \( \det(A) \neq 0 \). De plus, si \( A \) est inversible :
\det(A^{-1}) = \frac{1}{\det(A)}
\]
Ce théorème est fondamental : il relie l’algèbre linéaire (inversibilité) à un simple test numérique (signe du déterminant). En pratique, calculer le déterminant avant de tenter d’inverser une matrice vous fera gagner beaucoup de temps.
Calcul du déterminant : les quatre grandes méthodes
Il n’existe pas une seule façon de procéder. Selon la taille de la matrice, sa structure (beaucoup de zéros, forme triangulaire, symétrie…) et le contexte (calcul à la main ou démonstration théorique), on choisira la méthode la plus adaptée pour le calcul du déterminant.
Méthode 1 : Déterminant d’une matrice 2×2
C’est la formule de base, point de départ de toutes les autres. Pour une matrice \( 2 \times 2 \) :
\det\begin{pmatrix} a & b \\ c & d \end{pmatrix} = ad – bc
\]
On forme le produit de la diagonale principale (\( ad \)) et on soustrait le produit de la diagonale secondaire (\( bc \)). Simple, mais il faut faire attention à l’ordre : \( ad – bc \neq bc – ad \).
Méthode 2 : Règle de Sarrus pour les matrices 3×3
La règle de Sarrus (du mathématicien Pierre-Frédéric Sarrus, 1798–1861) est un procédé mnémotechnique visuel pour calculer le déterminant d’une matrice \( 3 \times 3 \). On écrit la matrice, puis on répète ses deux premières colonnes à droite :
\begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix}
= aei + bfg + cdh – ceg – bdi – afh
\]
Pour ne pas apprendre cette formule par cœur, voici la procédure visuelle :
- Recopiez les deux premières colonnes à droite de la matrice.
- Tracez les trois diagonales descendantes (de gauche à droite) : leurs produits sont comptés avec le signe \( + \).
- Tracez les trois diagonales montantes (de droite à gauche) : leurs produits sont comptés avec le signe \( – \).
- Faites la somme algébrique des six produits.
⚠ Attention ! La règle de Sarrus ne fonctionne que pour les matrices \( 3 \times 3 \). Il est tentant de vouloir l’étendre aux matrices \( 4 \times 4 \) ou plus — c’est une erreur classique et le résultat serait faux. Pour les tailles supérieures, on utilise le développement par cofacteurs ou le pivot de Gauss.
Méthode 3 : Développement par cofacteurs (formule de Laplace)
Mineur et cofacteur
Soit \( A \in \mathcal{M}_n(\mathbb{K}) \). Le mineur \( M_{i,j} \) est le déterminant de la matrice \( (n-1) \times (n-1) \) obtenue en supprimant la \( i \)-ème ligne et la \( j \)-ème colonne de \( A \). Le cofacteur associé est :
C_{i,j} = (-1)^{i+j} \, M_{i,j}
\]
Le facteur \( (-1)^{i+j} \) est un damier de signes : \( + \) si \( i+j \) est pair, \( – \) si \( i+j \) est impair. Pour ne pas se tromper, on visualise le motif suivant :
\begin{pmatrix} + & – & + & \cdots \\ – & + & – & \cdots \\ + & – & + & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{pmatrix}
\]
Formule de Laplace : développement suivant une ligne ou une colonne
Pour toute ligne \( i \) ou colonne \( j \) fixée :
\det(A) = \sum_{j=1}^{n} a_{i,j} \, C_{i,j}
\qquad \text{(développement suivant la ligne } i\text{)}
\]
\det(A) = \sum_{i=1}^{n} a_{i,j} \, C_{i,j}
\qquad \text{(développement suivant la colonne } j\text{)}
\]
Conseil pratique : choisissez toujours la ligne ou la colonne qui contient le plus grand nombre de zéros. Chaque zéro annule un terme, ce qui réduit considérablement le travail.
Méthode 4 : Pivot de Gauss : la méthode générale
La méthode du pivot de Gauss est la plus puissante et la seule vraiment efficace pour les matrices de grande taille (\( n \ge 4 \)). Elle consiste à transformer la matrice en une matrice triangulaire supérieure par des opérations élémentaires sur les lignes (ou colonnes), puis à lire le déterminant comme le produit des éléments diagonaux.
Déterminant d’une matrice triangulaire
Si \( T \) est une matrice triangulaire supérieure (ou inférieure), son déterminant est simplement le produit des termes diagonaux :
\det(T) = t_{11} \cdot t_{22} \cdot \ldots \cdot t_{nn} = \prod_{i=1}^{n} t_{ii}
\]
La stratégie est donc la suivante : on échelonne la matrice par des opérations élémentaires sur les lignes, en notant soigneusement leur effet sur le déterminant :
- \( L_i \leftarrow L_i + \lambda L_j \) (\( i \neq j \)) : le déterminant est inchangé.
- \( L_i \leftarrow \lambda L_i \) : le déterminant est multiplié par \( \lambda \).
- \( L_i \leftrightarrow L_j \) : le déterminant est multiplié par \( -1 \).
Une fois la matrice triangulaire obtenue, on applique le produit diagonal, puis on corrige avec les facteurs accumulés lors de l’échelonnage.
Preuve : le déterminant d’une matrice triangulaire est le produit des termes diagonaux
Voici une démonstration rigoureuse, par récurrence sur \( n \), du résultat fondamental qui justifie la méthode du pivot de Gauss.
Initialisation (\( n = 1 \)) : Toute matrice \( 1 \times 1 \) est triangulaire. Son déterminant est le seul coefficient \( a_{11} \), ce qui est bien le produit de l’unique terme diagonal. ✓
Hérédité : Supposons le résultat vrai pour toute matrice triangulaire de taille \( (n-1) \times (n-1) \). Soit \( T \in \mathcal{M}_n(\mathbb{K}) \) triangulaire supérieure. On développe \( \det(T) \) selon la première colonne :
\det(T) = t_{11} \cdot C_{1,1} + \underbrace{t_{21} \cdot C_{2,1} + \cdots + t_{n1} \cdot C_{n1}}_{= 0 \text{ car } T \text{ triangulaire sup.} \Rightarrow t_{i1}=0 \text{ pour } i \ge 2}
\]
Il reste donc \( \det(T) = t_{11} \cdot C_{1,1} = t_{11} \cdot \det(T_{11}) \), où \( T_{11} \) est la sous-matrice triangulaire supérieure de taille \( (n-1) \times (n-1) \). Par hypothèse de récurrence :
\det(T_{11}) = t_{22} \cdot t_{33} \cdots t_{nn}
\]
Donc \( \det(T) = t_{11} \cdot t_{22} \cdots t_{nn} = \prod_{i=1}^n t_{ii} \). La récurrence est établie. ∎
Application : règle de Cramer et systèmes linéaires
La règle de Cramer est l’une des applications directes du calcul du déterminant. Elle donne une formule explicite pour la solution unique d’un système carré \( Ax = b \) lorsque \( \det(A) \neq 0 \).
Théorème : Règle de Cramer
Soit \( Ax = b \) un système de \( n \) équations à \( n \) inconnues avec \( \det(A) \neq 0 \). Alors l’unique solution \( (x_1, x_2, \ldots, x_n) \) est donnée par :
x_j = \frac{\det(A_j)}{\det(A)}, \qquad j = 1, 2, \ldots, n
\]
où \( A_j \) est la matrice obtenue en remplaçant la \( j \)-ème colonne de \( A \) par le vecteur \( b \).
En pratique, la règle de Cramer est peu utilisée pour de grands systèmes (le pivot de Gauss est bien plus efficace), mais elle est précieuse lorsque les coefficients dépendent d’un paramètre, ou pour les démonstrations théoriques.
⚠ Erreur fréquente : Certains élèves appliquent la règle de Cramer sans vérifier d’abord que \( \det(A) \neq 0 \). Si le déterminant est nul, la matrice est non inversible et la règle ne s’applique pas — le système peut alors avoir zéro ou une infinité de solutions.
Erreurs fréquentes dans le calcul du déterminant
⚠ Confondre \( \det(A + B) \) et \( \det(A) + \det(B) \) : Le déterminant n’est pas linéaire par rapport à l’addition de matrices entières. On a \( \det(A+B) \neq \det(A) + \det(B) \) en général. La formule \( \det(AB) = \det(A)\det(B) \) ne se transpose pas à l’addition.
⚠ Appliquer Sarrus à une matrice 4×4 : La règle de Sarrus n’est valable qu’en dimension 3. En dimension 4 et au-delà, elle ne donne pas le bon résultat. Utilisez le développement par cofacteurs ou le pivot de Gauss.
⚠ Oublier de compter les échanges de lignes : Lors d’un pivotage, chaque échange de deux lignes multiplie le déterminant par \( -1 \). Oublier cela peut inverser le signe du résultat final.
⚠ Factoriser incorrectement : Si l’on factorise un scalaire \( \lambda \) hors d’une seule ligne, le déterminant est divisé par \( \lambda \). Ce n’est pas la même chose que factoriser \( \lambda \) hors de la matrice entière, ce qui multiplierait le déterminant par \( \lambda^n \).
Conclusion : Maîtriser le calcul du déterminant
Le calcul du déterminant d’une matrice repose sur quelques idées simples mais puissantes : la formule de Leibniz en fonde la théorie, les opérations élémentaires sur les lignes et les colonnes en constituent le moteur pratique. En dimension 2, une formule suffit. En dimension 3, la règle de Sarrus offre un raccourci visuel. Pour les matrices de taille quelconque, le développement par cofacteurs (méthode de Laplace) et le pivot de Gauss sont les deux outils à maîtriser absolument.
Retenez surtout que le déterminant n’est pas qu’un outil de calcul : c’est une fenêtre sur la géométrie (aire, volume orienté), sur l’algèbre (inversibilité, rang) et sur l’analyse (changements de variables dans les intégrales multiples via le jacobien). La maîtrise du calcul du déterminant est donc un investissement qui porte ses fruits dans toute la suite du cursus mathématique.