La réduction des endomorphismes constitue l’un des piliers fondamentaux de l’algèbre linéaire moderne. Cette technique permet de simplifier l’étude des applications linéaires en les exprimant dans une base adaptée, facilitant ainsi les calculs matriciels et la résolution de nombreux problèmes mathématiques et physiques. Que vous soyez étudiant en classes préparatoires, en licence de mathématiques ou simplement passionné d’algèbre, ce cours complet vous permettra de maîtriser tous les aspects de cette notion essentielle.
Dans ce cours, nous explorerons les différentes formes de réduction : la diagonalisation, la trigonalisation, ainsi que la réduction de Jordan. Nous verrons comment le polynôme caractéristique et les valeurs propres jouent un rôle central dans cette théorie, et nous étudierons des applications concrètes allant des systèmes d’équations différentielles aux suites récurrentes.
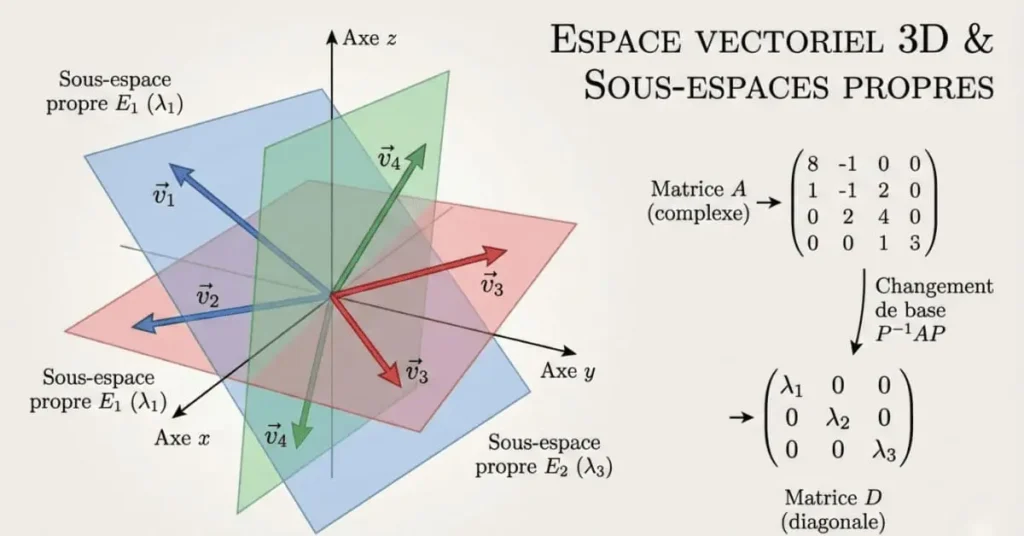
Qu’est-ce que la Réduction des Endomorphismes ?
Définition fondamentale
La réduction d’un endomorphisme consiste à trouver une base dans laquelle la matrice de cet endomorphisme prend une forme simplifiée, typiquement diagonale ou triangulaire. Formellement, soit \( E \) un espace vectoriel de dimension finie \( n \) sur un corps \( \mathbb{K} \) (généralement \( \mathbb{R} \) ou \( \mathbb{C} \)), et soit \( u \in \mathcal{L}(E) \) un endomorphisme de \( E \).
On cherche à déterminer une base \( \mathcal{B} = (e_1, e_2, \ldots, e_n) \) de \( E \) dans laquelle la matrice de \( u \) est la plus simple possible, c’est-à-dire possède un maximum de coefficients nuls.
Pourquoi réduire un endomorphisme ?
La réduction des endomorphismes répond à plusieurs objectifs fondamentaux en mathématiques et dans leurs applications. Premièrement, elle simplifie considérablement les calculs matriciels. Le calcul de puissances de matrices, opération fréquente en probabilités ou en systèmes dynamiques, devient trivial avec une matrice diagonale. En effet, si \( A = PDP^{-1} \) où \( D \) est diagonale, alors \( A^n = PD^nP^{-1} \), et calculer \( D^n \) se réduit à élever chaque coefficient diagonal à la puissance \( n \).
Deuxièmement, la réduction permet de comprendre la structure géométrique d’une transformation linéaire. Les sous-espaces propres révèlent les directions privilégiées de l’endomorphisme, celles où l’action se réduit à une simple homothétie. Cette vision géométrique est cruciale en mécanique quantique, où les espaces propres correspondent aux états stationnaires d’un système.
Enfin, cette technique est indispensable pour résoudre des systèmes d’équations différentielles linéaires, étudier la stabilité des systèmes dynamiques, ou encore analyser les algorithmes de page ranking comme celui utilisé par Google.
Éléments Propres : Valeurs Propres et Vecteurs Propres
Valeurs propres et vecteurs propres
Soit \( u \) un endomorphisme d’un espace vectoriel \( E \) sur un corps \( \mathbb{K} \).
- Un scalaire \( \lambda \in \mathbb{K} \) est appelé valeur propre de \( u \) s’il existe un vecteur non nul \( x \in E \) tel que \( u(x) = \lambda x \).
- Un vecteur non nul \( x \in E \) est appelé vecteur propre de \( u \) associé à la valeur propre \( \lambda \) si \( u(x) = \lambda x \).
- L’ensemble \( E_\lambda = \{ x \in E \mid u(x) = \lambda x \} \) est appelé sous-espace propre associé à la valeur propre \( \lambda \). C’est le noyau de l’endomorphisme \( u – \lambda \text{Id}_E \).
Propriétés fondamentales des sous-espaces propres
Les sous-espaces propres possèdent des propriétés remarquables qui constituent le fondement de la théorie de la réduction. La propriété la plus importante est que les sous-espaces propres associés à des valeurs propres distinctes sont en somme directe.
Théorème : Somme directe des sous-espaces propres
Soit \( u \) un endomorphisme de \( E \) admettant \( p \) valeurs propres distinctes \( \lambda_1, \lambda_2, \ldots, \lambda_p \). Les sous-espaces propres associés \( E_{\lambda_1}, E_{\lambda_2}, \ldots, E_{\lambda_p} \) sont en somme directe :
Démonstration : Montrons le résultat par récurrence sur \( p \). Pour \( p = 1 \), il n’y a rien à démontrer. Supposons le résultat vrai pour \( p \) valeurs propres distinctes. Considérons \( p+1 \) valeurs propres distinctes \( \lambda_1, \ldots, \lambda_{p+1} \). Il suffit de montrer que l’intersection de \( E_{\lambda_1} \oplus \cdots \oplus E_{\lambda_p} \) avec \( E_{\lambda_{p+1}} \) est réduite au vecteur nul.
Soit \( x \in (E_{\lambda_1} \oplus \cdots \oplus E_{\lambda_p}) \cap E_{\lambda_{p+1}} \). On peut écrire \( x = x_1 + \cdots + x_p \) avec \( x_i \in E_{\lambda_i} \) pour tout \( i \). Appliquons \( u \) :
Donc \( (\lambda_1 – \lambda_{p+1})x_1 + \cdots + (\lambda_p – \lambda_{p+1})x_p = 0 \). Par hypothèse de récurrence, cette somme étant directe et les coefficients \( \lambda_i – \lambda_{p+1} \) étant non nuls (car les valeurs propres sont distinctes), on obtient \( x_i = 0 \) pour tout \( i \), donc \( x = 0 \).
Exemple détaillé : Calcul de valeurs et vecteurs propres
Considérons la matrice suivante dans \( \mathcal{M}_3(\mathbb{R}) \) :
Étape 1 : Détermination des valeurs propres. Les valeurs propres sont les racines du polynôme caractéristique. Puisque \( A \) est triangulaire supérieure, ses valeurs propres sont les coefficients diagonaux : \( \lambda_1 = 2 \) (de multiplicité 2) et \( \lambda_2 = 3 \) (de multiplicité 1).
Étape 2 : Calcul du sous-espace propre \( E_2 \). Résolvons \( (A – 2I_3)X = 0 \) :
Ce système équivaut à \( y = 0 \) et \( z = 0 \). Donc \( E_2 = \text{Vect}\left\{ \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \right\} \). On remarque que \( \dim(E_2) = 1 < 2 = \text{mult}(2) \), ce qui indique que la matrice n'est pas diagonalisable.
Étape 3 : Calcul du sous-espace propre \( E_3 \). De même, on trouve \( E_3 = \text{Vect}\left\{ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right\} \).
Le Polynôme Caractéristique : Outil Central de la Réduction
Définition du polynôme caractéristique
Soit \( A \in \mathcal{M}_n(\mathbb{K}) \) une matrice carrée. Le polynôme caractéristique de \( A \) est défini par :
Pour un endomorphisme \( u \) d’un espace vectoriel \( E \) de dimension finie, le polynôme caractéristique \( \chi_u \) est défini comme le polynôme caractéristique de sa matrice dans n’importe quelle base de \( E \) (il est indépendant du choix de la base).
Propriétés essentielles du polynôme caractéristique
Le polynôme caractéristique possède plusieurs propriétés fondamentales qui en font l’outil privilégié pour l’étude de la réduction. Tout d’abord, c’est un polynôme de degré \( n \) dont le coefficient dominant est \( (-1)^n \). De plus, ses racines dans \( \mathbb{K} \) sont exactement les valeurs propres de la matrice ou de l’endomorphisme considéré.
Une propriété remarquable est que le polynôme caractéristique encode des informations sur la trace et le déterminant. En effet, si \( \chi_A(\lambda) = (-1)^n(\lambda^n – a_{n-1}\lambda^{n-1} + \cdots + (-1)^n a_0) \), alors la trace de \( A \) vaut \( a_{n-1} \) et son déterminant vaut \( a_0 \). Ceci découle du fait que la trace est la somme des valeurs propres et le déterminant est leur produit.
Théorème : Relation entre polynôme caractéristique et éléments propres
Soit \( A \in \mathcal{M}_n(\mathbb{K}) \) une matrice carrée. Un scalaire \( \lambda \in \mathbb{K} \) est une valeur propre de \( A \) si et seulement si \( \chi_A(\lambda) = 0 \).
Démonstration : Par définition, \( \lambda \) est valeur propre si et seulement s’il existe \( X \neq 0 \) tel que \( AX = \lambda X \), c’est-à-dire \( (A – \lambda I_n)X = 0 \). Ceci équivaut à dire que \( A – \lambda I_n \) n’est pas inversible, donc \( \det(A – \lambda I_n) = 0 \), soit \( \chi_A(\lambda) = 0 \).
Calcul pratique du polynôme caractéristique
Pour les matrices de petite taille, on peut calculer directement le déterminant. Pour une matrice \( 2 \times 2 \), on a une formule simple utilisant la trace et le déterminant :
Pour les matrices triangulaires ou diagonales, le calcul est immédiat : le polynôme caractéristique est le produit des termes \( (\lambda – a_{ii}) \) où les \( a_{ii} \) sont les coefficients diagonaux.
Polynôme caractéristique scindé
On dit qu’un polynôme est scindé sur \( \mathbb{K} \) s’il se factorise complètement en produit de polynômes de degré 1 dans \( \mathbb{K}[X] \). Autrement dit :
où \( \lambda_1, \ldots, \lambda_r \) sont les valeurs propres distinctes et \( m_i \) est la multiplicité algébrique de \( \lambda_i \). Sur le corps des complexes \( \mathbb{C} \), tout polynôme est scindé grâce au théorème fondamental de l’algèbre. En revanche, sur \( \mathbb{R} \), ce n’est pas toujours le cas.
Diagonalisation des Endomorphismes et des Matrices
Endomorphisme diagonalisable
Un endomorphisme \( u \) d’un espace vectoriel \( E \) de dimension finie \( n \) est dit diagonalisable s’il existe une base \( \mathcal{B} \) de \( E \) dans laquelle la matrice de \( u \) est diagonale.
De manière équivalente, une matrice \( A \in \mathcal{M}_n(\mathbb{K}) \) est diagonalisable s’il existe une matrice inversible \( P \in GL_n(\mathbb{K}) \) et une matrice diagonale \( D \) telles que :
La matrice \( P \) est appelée matrice de passage, et ses colonnes sont constituées des vecteurs propres de \( A \). La matrice \( D \) a pour coefficients diagonaux les valeurs propres correspondantes.
Conditions de diagonalisabilité
La question centrale de la réduction est de déterminer quand un endomorphisme est diagonalisable. Plusieurs critères existent, du plus simple au plus général.
Théorème : Condition suffisante de diagonalisabilité
Si le polynôme caractéristique d’un endomorphisme \( u \) de \( E \) (avec \( \dim E = n \)) est scindé à racines simples, alors \( u \) est diagonalisable.
Démonstration : Si \( \chi_u \) admet \( n \) racines distinctes \( \lambda_1, \ldots, \lambda_n \), alors pour chaque \( i \), il existe au moins un vecteur propre \( e_i \) associé à \( \lambda_i \). Les vecteurs propres associés à des valeurs propres distinctes étant linéairement indépendants, la famille \( (e_1, \ldots, e_n) \) est libre dans un espace de dimension \( n \), donc c’est une base de vecteurs propres.
Théorème : Caractérisation complète de la diagonalisabilité
Un endomorphisme \( u \) d’un espace \( E \) de dimension \( n \) est diagonalisable si et seulement si les deux conditions suivantes sont satisfaites :
- Le polynôme caractéristique \( \chi_u \) est scindé sur \( \mathbb{K} \)
- Pour chaque valeur propre \( \lambda \), la dimension du sous-espace propre \( E_\lambda \) est égale à la multiplicité algébrique de \( \lambda \) dans \( \chi_u \)
Autrement dit : \( \dim(E_\lambda) = \text{mult}(\lambda) \) pour toute valeur propre \( \lambda \).
Démonstration : Si \( u \) est diagonalisable, il existe une base de vecteurs propres. Le nombre de vecteurs propres associés à chaque valeur propre \( \lambda \) dans cette base doit égaler \( \dim(E_\lambda) \). La somme de ces dimensions doit valoir \( n \), et d’autre part la somme des multiplicités vaut aussi \( n \) (degré du polynôme). D’où l’égalité pour chaque valeur propre.
Réciproquement, si les conditions sont satisfaites, en prenant une base de chaque sous-espace propre, on obtient au total \( \sum \text{mult}(\lambda_i) = n \) vecteurs linéairement indépendants (car les sous-espaces propres sont en somme directe), qui forment donc une base de vecteurs propres.
Méthode pratique de diagonalisation
Pour diagonaliser une matrice \( A \in \mathcal{M}_n(\mathbb{K}) \), on suit les étapes suivantes :
- Calculer le polynôme caractéristique \( \chi_A(\lambda) = \det(A – \lambda I_n) \)
- Déterminer les valeurs propres en résolvant \( \chi_A(\lambda) = 0 \)
- Vérifier si \( \chi_A \) est scindé sur \( \mathbb{K} \). Si non, \( A \) n’est pas diagonalisable sur \( \mathbb{K} \)
- Pour chaque valeur propre \( \lambda_i \), calculer le sous-espace propre \( E_{\lambda_i} = \text{Ker}(A – \lambda_i I_n) \) en résolvant le système linéaire \( (A – \lambda_i I_n)X = 0 \)
- Déterminer une base de chaque \( E_{\lambda_i} \)
- Vérifier la condition de diagonalisabilité : \( \sum \dim(E_{\lambda_i}) = n \)
- Construire \( P \) et \( D \) : les colonnes de \( P \) sont les vecteurs propres trouvés, et \( D \) est la matrice diagonale des valeurs propres correspondantes
Exemple complet de diagonalisation
Soit la matrice suivante :
Étape 1 : Le polynôme caractéristique est \( \chi_B(\lambda) = (1-\lambda)^2(2-\lambda) \).
Étape 2 : Les valeurs propres sont \( \lambda_1 = 1 \) (double) et \( \lambda_2 = 2 \) (simple).
Étape 3 : Pour \( \lambda_1 = 1 \) :
Le système donne \( y = 0 \) et \( z = 0 \), donc \( E_1 = \text{Vect}\left\{ \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \right\} \). On a \( \dim(E_1) = 1 \neq 2 = \text{mult}(1) \), donc \( B \) n’est pas diagonalisable.
Cet exemple illustre un cas important : une matrice peut avoir toutes ses valeurs propres réelles et pourtant ne pas être diagonalisable. La condition sur les dimensions des sous-espaces propres est essentielle.
Trigonalisation : Alternative à la Diagonalisation
Endomorphisme trigonalisable
Un endomorphisme \( u \) d’un espace vectoriel \( E \) de dimension finie est dit trigonalisable (ou triangularisable) s’il existe une base de \( E \) dans laquelle la matrice de \( u \) est triangulaire supérieure.
Une matrice \( A \in \mathcal{M}_n(\mathbb{K}) \) est trigonalisable sur \( \mathbb{K} \) s’il existe \( P \in GL_n(\mathbb{K}) \) et une matrice triangulaire supérieure \( T \) telles que :
Critère de trigonalisabilité
Théorème fondamental de trigonalisation
Un endomorphisme \( u \) d’un espace vectoriel \( E \) de dimension finie est trigonalisable si et seulement si son polynôme caractéristique est scindé sur \( \mathbb{K} \).
Corollaire immédiat : Sur le corps \( \mathbb{C} \) des nombres complexes, tout endomorphisme est trigonalisable (car tout polynôme à coefficients complexes est scindé sur \( \mathbb{C} \)).
Démonstration par récurrence : Soit \( n = \dim E \). Si \( n = 1 \), tout endomorphisme est représenté par une matrice \( 1 \times 1 \), donc triangulaire. Supposons le résultat vrai pour tout espace de dimension \( \leq n-1 \).
Soit \( u \) un endomorphisme de \( E \) dont le polynôme caractéristique est scindé. Alors \( \chi_u \) admet au moins une racine \( \lambda \in \mathbb{K} \). Il existe donc un vecteur propre \( e_1 \) non nul tel que \( u(e_1) = \lambda e_1 \). Complétons \( e_1 \) en une base \( (e_1, e_2, \ldots, e_n) \) de \( E \).
Soit \( F = \text{Vect}(e_2, \ldots, e_n) \). Dans la base choisie, la matrice de \( u \) s’écrit sous forme triangulaire par blocs. Le polynôme caractéristique de la restriction de \( u \) à \( F \) divise \( \chi_u \), donc est aussi scindé. Par hypothèse de récurrence, cette restriction est trigonalisable, ce qui permet de conclure.
Relation entre diagonalisation et trigonalisation
Toute matrice diagonalisable est évidemment trigonalisable, puisqu’une matrice diagonale est un cas particulier de matrice triangulaire. L’intérêt de la trigonalisation réside dans le fait qu’elle est possible pour une classe beaucoup plus large d’endomorphismes. Sur \( \mathbb{C} \), elle est même toujours possible.
Cependant, la trigonalisation est moins puissante que la diagonalisation pour les calculs pratiques. Par exemple, calculer les puissances d’une matrice triangulaire non diagonale reste complexe, contrairement au cas diagonal où le calcul est immédiat.
Exemple de trigonalisation
Reprenons la matrice \( B \) de l’exemple précédent, qui n’était pas diagonalisable :
Cette matrice est déjà sous forme triangulaire supérieure ! Elle est donc trigonalisable (avec \( P = I_3 \) et \( T = B \)). Cet exemple montre qu’une matrice peut être trigonalisable sans être diagonalisable.
Réduction de Jordan : La Forme Canonique Ultime
Lorsqu’un endomorphisme n’est pas diagonalisable mais que son polynôme caractéristique est scindé, on peut aller au-delà de la simple trigonalisation en déterminant la forme normale de Jordan, qui est la forme réduite la plus simple possible.
Bloc de Jordan
Un bloc de Jordan de valeur propre \( \lambda \) et de taille \( p \) est une matrice carrée \( p \times p \) de la forme :
La diagonale contient la valeur propre \( \lambda \), la sur-diagonale contient des 1, et tous les autres coefficients sont nuls.
Théorème de Jordan
Soit \( u \) un endomorphisme d’un espace vectoriel \( E \) de dimension finie \( n \) dont le polynôme caractéristique est scindé. Alors il existe une base de \( E \) dans laquelle la matrice de \( u \) est diagonale par blocs, chaque bloc étant un bloc de Jordan :
où \( \lambda_1, \ldots, \lambda_s \) sont les valeurs propres de \( u \) (non nécessairement distinctes). De plus, cette forme est unique à l’ordre près des blocs.
Interprétation de la réduction de Jordan
La réduction de Jordan encode des informations précises sur la structure de l’endomorphisme. Pour chaque valeur propre \( \lambda \) :
- La multiplicité algébrique de \( \lambda \) (son ordre dans \( \chi_u \)) est égale à la somme des tailles des blocs de Jordan associés à \( \lambda \)
- La multiplicité géométrique de \( \lambda \) (dimension de \( E_\lambda \)) est égale au nombre de blocs de Jordan associés à \( \lambda \)
- La taille du plus grand bloc de Jordan pour \( \lambda \) correspond à la multiplicité de \( \lambda \) dans le polynôme minimal
Une matrice est diagonalisable si et seulement si tous ses blocs de Jordan sont de taille 1.
Décomposition de Dunford
La réduction de Jordan s’appuie sur un résultat fondamental :
Théorème de décomposition de Dunford
Soit \( u \) un endomorphisme dont le polynôme caractéristique est scindé. Il existe un unique couple \( (d, n) \) d’endomorphismes tel que :
- \( u = d + n \)
- \( d \) est diagonalisable
- \( n \) est nilpotent (c’est-à-dire \( n^k = 0 \) pour un certain entier \( k \))
- \( d \circ n = n \circ d \) (ils commutent)
De plus, \( d \) et \( n \) sont des polynômes en \( u \).
Cette décomposition montre que tout endomorphisme trigonalisable peut être vu comme la somme d’une partie diagonalisable et d’une partie nilpotente qui commutent. C’est le point de départ de la construction de la forme de Jordan.
Applications Pratiques de la Réduction
Calcul de puissances de matrices
L’une des applications les plus immédiates de la diagonalisation est le calcul de puissances de matrices. Si \( A = PDP^{-1} \) avec \( D \) diagonale, alors :
Or, calculer \( D^n \) est trivial : si \( D = \text{diag}(\lambda_1, \ldots, \lambda_k) \), alors \( D^n = \text{diag}(\lambda_1^n, \ldots, \lambda_k^n) \).
Exemple : Calculons \( A^{10} \) pour \( A = \begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix} \).
Le polynôme caractéristique est \( \chi_A(\lambda) = \lambda^2 – 7\lambda + 10 = (\lambda-2)(\lambda-5) \). Les valeurs propres sont 2 et 5. On trouve que \( A = P \begin{pmatrix} 2 & 0 \\ 0 & 5 \end{pmatrix} P^{-1} \) avec \( P = \begin{pmatrix} 1 & 1 \\ 2 & 1 \end{pmatrix} \).
Donc :
Résolution de systèmes d’équations différentielles linéaires
Considérons le système différentiel linéaire à coefficients constants :
Ce système s’écrit matriciellement \( X'(t) = AX(t) \) avec \( X(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} \) et \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \).
Si \( A \) est diagonalisable avec \( A = PDP^{-1} \), en posant \( Y(t) = P^{-1}X(t) \), le système devient \( Y'(t) = DY(t) \), qui est découplé. Chaque composante \( y_i(t) \) vérifie \( y_i'(t) = \lambda_i y_i(t) \), dont la solution est \( y_i(t) = y_i(0) e^{\lambda_i t} \).
On obtient finalement \( X(t) = P e^{Dt} P^{-1} X(0) \), où \( e^{Dt} = \text{diag}(e^{\lambda_1 t}, \ldots, e^{\lambda_n t}) \).
Suites récurrentes linéaires
Soit la suite définie par la récurrence \( u_{n+2} = 5u_{n+1} – 6u_n \) avec \( u_0 = 0 \) et \( u_1 = 1 \).
On peut réécrire ce problème matriciellement : \( X_{n+1} = AX_n \) avec \( X_n = \begin{pmatrix} u_{n+1} \\ u_n \end{pmatrix} \) et \( A = \begin{pmatrix} 5 & -6 \\ 1 & 0 \end{pmatrix} \).
Le polynôme caractéristique de \( A \) est \( \chi_A(\lambda) = \lambda^2 – 5\lambda + 6 = (\lambda-2)(\lambda-3) \). Après diagonalisation, on trouve que les valeurs propres sont 2 et 3.
La solution générale est de la forme \( u_n = \alpha \cdot 2^n + \beta \cdot 3^n \). Avec les conditions initiales, on obtient \( \alpha = -1 \) et \( \beta = 1 \), donc :
Cas Particuliers et Matrices Remarquables
Matrices symétriques réelles
Théorème spectral pour les matrices symétriques réelles
Toute matrice symétrique réelle est diagonalisable dans une base orthonormée, et toutes ses valeurs propres sont réelles.
Plus précisément, si \( A \in \mathcal{M}_n(\mathbb{R}) \) est symétrique, il existe une matrice orthogonale \( P \) (c’est-à-dire \( P^T P = I_n \)) et une matrice diagonale \( D \) telles que \( A = PDP^T \).
Ce résultat est fondamental en géométrie et en physique. Il signifie que toute forme quadratique peut être exprimée sous forme canonique dans un repère orthonormé approprié. Les axes de ce repère sont les directions propres, et les valeurs propres donnent les coefficients dans l’expression canonique.
Projecteurs et symétries
Un projecteur \( p \) (vérifiant \( p^2 = p \)) est toujours diagonalisable, avec pour valeurs propres 0 et 1 uniquement. En effet, si \( p(x) = \lambda x \), alors \( p^2(x) = \lambda^2 x = p(x) = \lambda x \), donc \( \lambda(\lambda – 1) = 0 \).
De même, une symétrie \( s \) (vérifiant \( s^2 = \text{Id} \)) est diagonalisable avec pour valeurs propres 1 et -1. Les sous-espaces propres correspondent respectivement aux éléments invariants et aux éléments changés de signe.
Endomorphismes nilpotents
Un endomorphisme \( n \) est dit nilpotent s’il existe un entier \( k \) tel que \( n^k = 0 \). Un endomorphisme nilpotent non nul n’est jamais diagonalisable (car sa seule valeur propre est 0, mais son noyau n’est pas l’espace tout entier).
Cependant, tout endomorphisme nilpotent est trigonalisable avec une matrice triangulaire stricte (diagonale nulle). La réduction de Jordan d’un endomorphisme nilpotent ne contient que des blocs de Jordan de valeur propre 0.
Résumé et Points Clés à Retenir
La réduction des endomorphismes est une théorie riche qui unifie de nombreux concepts de l’algèbre linéaire. Retenons les points essentiels :
- La réduction vise à exprimer un endomorphisme dans une base où sa matrice est simple (diagonale, triangulaire, ou forme de Jordan)
- Les valeurs propres sont les racines du polynôme caractéristique et déterminent le comportement de l’endomorphisme
- Les sous-espaces propres sont en somme directe et fournissent les directions privilégiées de la transformation
- La diagonalisabilité requiert que le polynôme caractéristique soit scindé et que chaque multiplicité géométrique égale la multiplicité algébrique
- La trigonalisation est toujours possible sur \( \mathbb{C} \) dès que le polynôme caractéristique est scindé
- La forme de Jordan est la forme canonique la plus fine pour les endomorphismes dont le polynôme caractéristique est scindé
- Les applications pratiques incluent le calcul de puissances, la résolution de systèmes différentiels et l’étude des suites récurrentes
La maîtrise de ces concepts est indispensable pour aborder des domaines avancés comme l’analyse fonctionnelle, la théorie des groupes de Lie, ou encore la mécanique quantique.